Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Графическое решение квадратных уравнений
Содержание
1 способ х2 – 2х – 3 = 0Построим график функции y = x2 – 2x – 3 1)Имеем: a = 1, b = -2, x0 = -b ÷ 2a =
Слайды и текст этой презентации
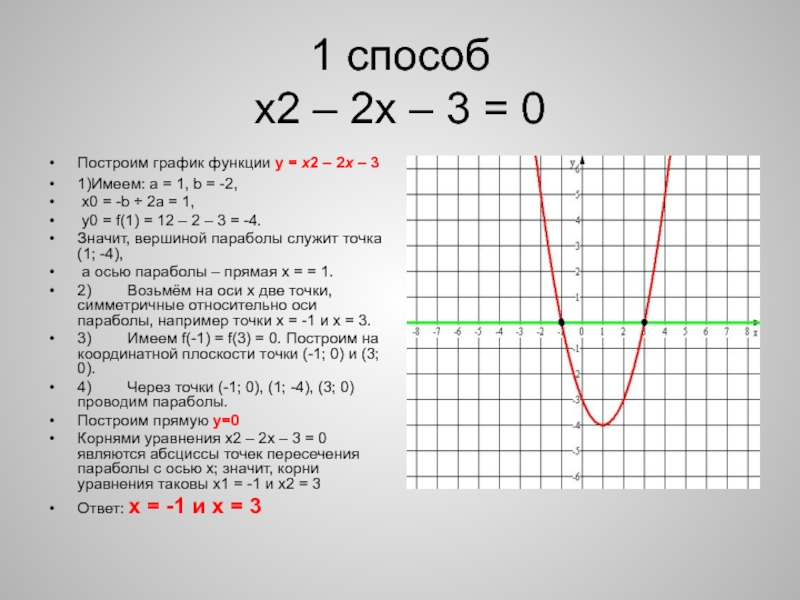
Слайд 21 способ
х2 – 2х – 3 = 0
Построим график функции
y = x2 – 2x – 3
1)Имеем: a =
1, b = -2,x0 = -b ÷ 2a = 1,
y0 = f(1) = 12 – 2 – 3 = -4.
Значит, вершиной параболы служит точка (1; -4),
а осью параболы – прямая x = = 1.
2) Возьмём на оси x две точки, симметричные относительно оси параболы, например точки x = -1 и x = 3.
3) Имеем f(-1) = f(3) = 0. Построим на координатной плоскости точки (-1; 0) и (3; 0).
4) Через точки (-1; 0), (1; -4), (3; 0) проводим параболы.
Построим прямую y=0
Корнями уравнения x2 – 2x – 3 = 0 являются абсциссы точек пересечения параболы с осью х; значит, корни уравнения таковы x1 = -1 и x2 = 3
Ответ: х = -1 и х = 3
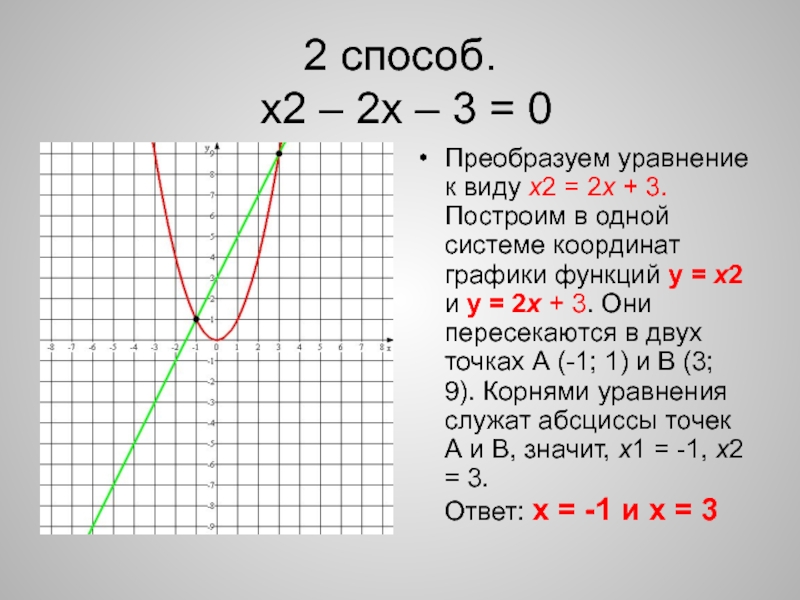
Слайд 32 способ.
х2 – 2х – 3 = 0
Преобразуем уравнение
к виду x2 = 2x + 3. Построим в одной
системе координат графики функций y = x2 и y = 2x + 3. Они пересекаются в двух точках А (-1; 1) и В (3; 9). Корнями уравнения служат абсциссы точек А и В, значит, х1 = -1, х2 = 3. Ответ: х = -1 и х = 3Слайд 43 способ.
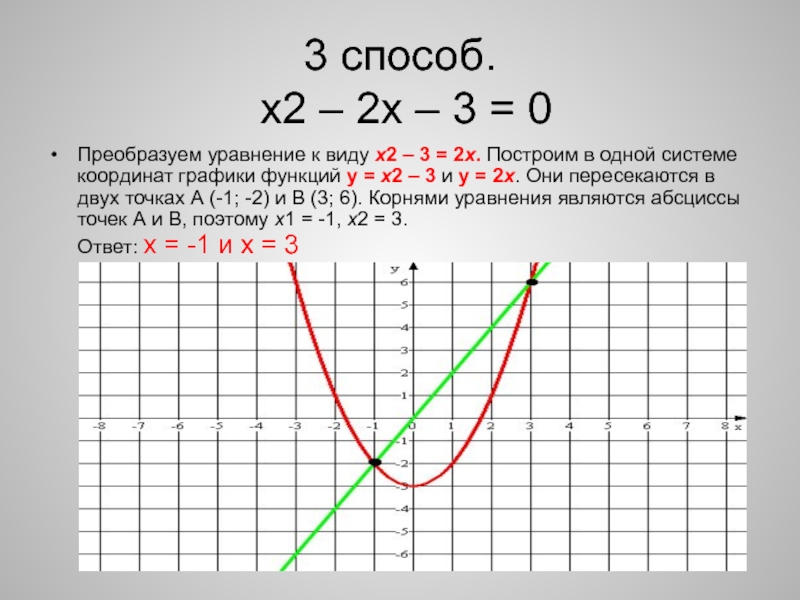
х2 – 2х – 3 = 0
Преобразуем уравнение
к виду х2 – 3 = 2х. Построим в одной
системе координат графики функций у = х2 – 3 и у = 2х. Они пересекаются в двух точках А (-1; -2) и В (3; 6). Корнями уравнения являются абсциссы точек А и В, поэтому х1 = -1, х2 = 3. Ответ: х = -1 и х = 3Слайд 54 способ
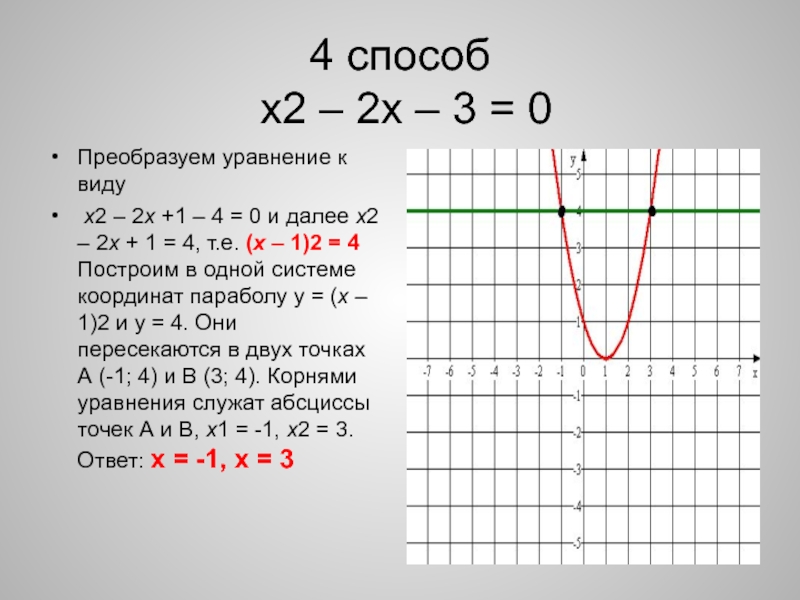
х2 – 2х – 3 = 0
Преобразуем уравнение
к виду
х2 – 2х +1 – 4 = 0
и далее х2 – 2х + 1 = 4, т.е. (х – 1)2 = 4
Построим в одной системе координат параболу у = (х – 1)2 и у = 4. Они пересекаются в двух точках А (-1; 4) и В (3; 4). Корнями уравнения служат абсциссы точек А и В, х1 = -1, х2 = 3.
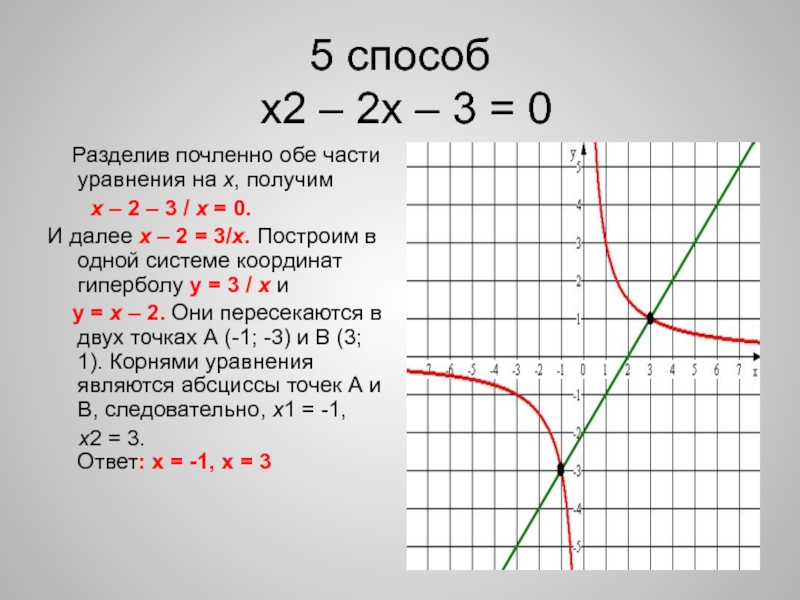
Ответ: х = -1, х = 3 Слайд 65 способ
х2 – 2х – 3 = 0
Разделив почленно обе части уравнения на х, получим
х – 2 – 3 / х = 0. И далее х – 2 = 3/х. Построим в одной системе координат гиперболу у = 3 / х и
у = х – 2. Они пересекаются в двух точках А (-1; -3) и В (3; 1). Корнями уравнения являются абсциссы точек А и В, следовательно, х1 = -1,
х2 = 3. Ответ: х = -1, х = 3
Слайд 7Итак, квадратное уравнение x2 – 2x – 3 = 0
мы решили графически пятью способами. Давайте проанализируем, в чем суть
этих способовСлайд 8Вывод.
Я решал одно и то же уравнение графически, строя различные
графики, но получил одни и те же корни. Это говорит
о том, что независимо от выбора способа решения уравнения, корни не изменяются.Заметим, что первые четыре способа применимы к любым уравнениям вида ах2 + bх + с = 0, а пятый - только к тем, у которых с не равен 0. На практике можно выбирать тот способ, который нам кажется наиболее приспособленным к данному уравнению или который нам больше нравится (или более понятен).
Графические способы решения квадратного уравнения красивы и приятны, но не дают стопроцентной гарантии решения любого квадратного уравнения.