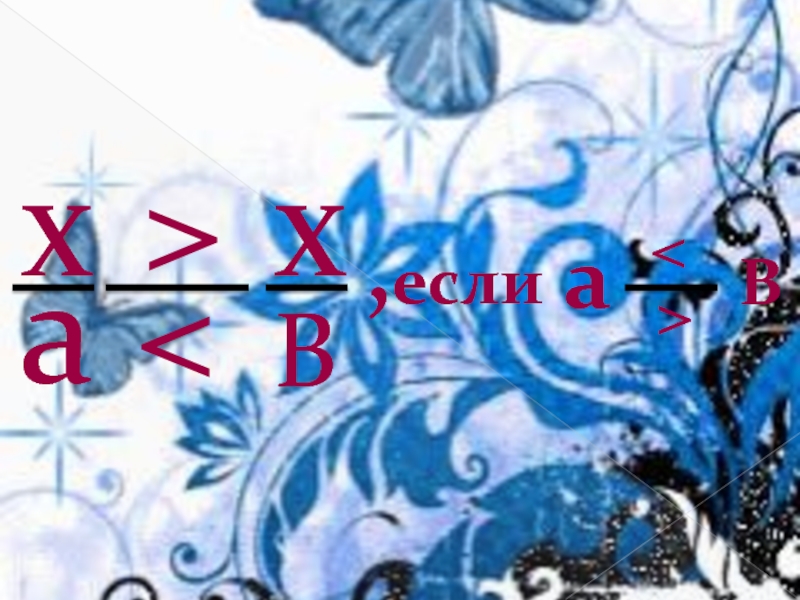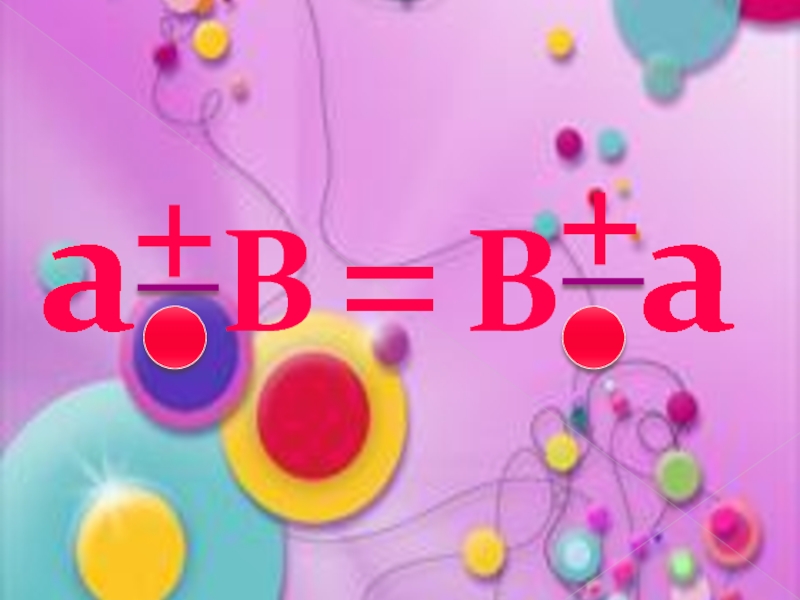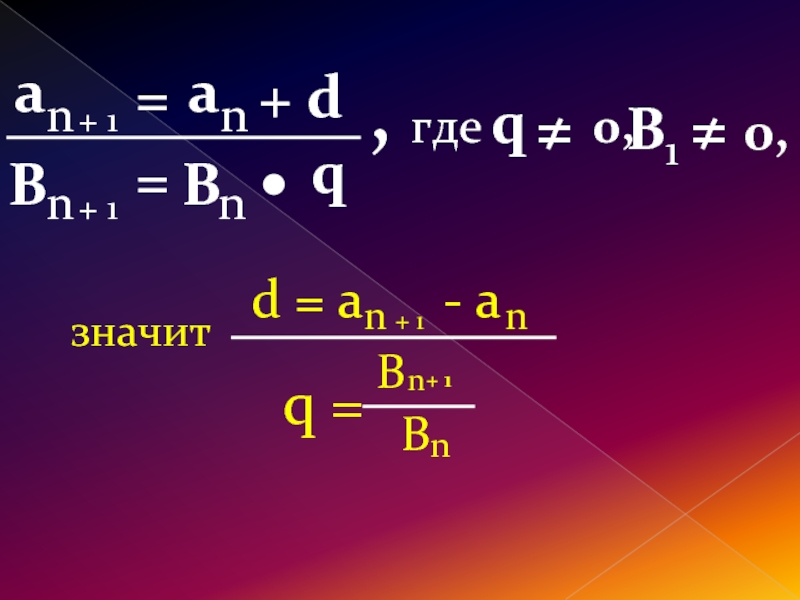Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Применение параллельной записи
Содержание
- 1. Применение параллельной записи
- 2. ЦельСнятие перегрузки.Выделение главного.
- 3. В записях рассуждений я использую экономную форму:повторяющиеся слова записываю лишь один раз
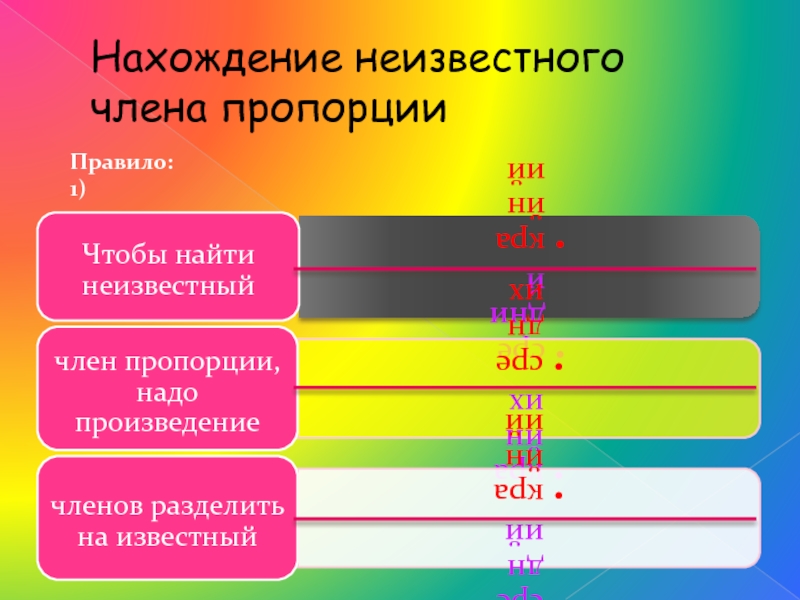
- 4. Нахождение неизвестного члена пропорцииПравило:1)
- 5. 2)kx
- 6. Сравнение обыкновенных дробейИз двух дробей с равными числителями та, у которой знаменатель
- 7. ,еслиaB
- 8. Переместительные законы сложения и умноженияслагаемыхмножителейОт перестановкиСуммапроизведениеНе изменяется
- 9. Слайд 9
- 10. умножение и деление многочлена на число.Чтобы
- 11. Арифметическая и геометрическая прогрессии.1. Даны последовательности:
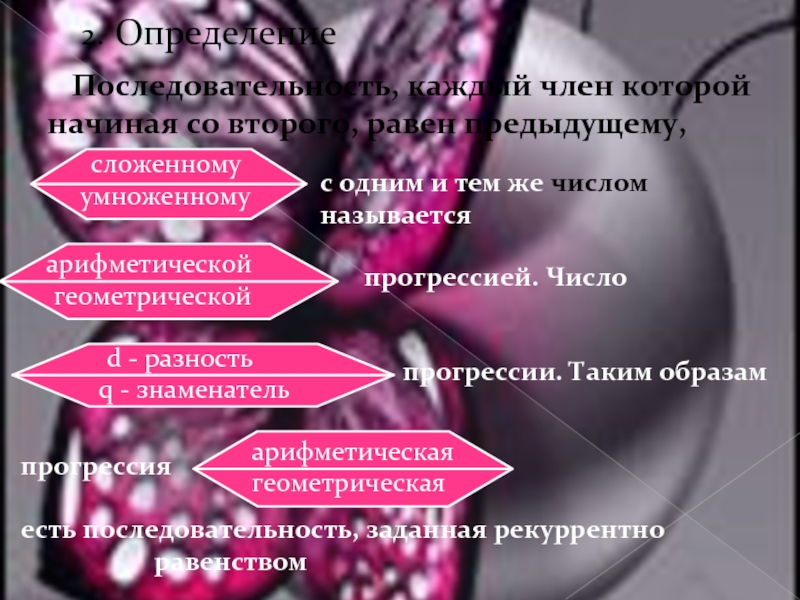
- 12. 2. Определение Последовательность, каждый член которой начиная
- 13. Слайд 13
- 14. 3. СвойстваФормула n –
- 15. Формула n – го члена для арифметической
- 16. Характеристическое свойствоПоследовательность является
- 17. Свойство прямой и обратной пропорциональностей.Если две величины
- 18. Установление взаимосвязи между понятиями
- 19. Слайд 19
- 20. В результате эксперимента были достигнуты все цели поставленные в начале!!!КОНЕЦ.
- 21. Скачать презентанцию
ЦельСнятие перегрузки.Выделение главного.
Слайды и текст этой презентации
Слайд 3В записях рассуждений я использую экономную форму:
повторяющиеся слова записываю лишь
один раз
Слайд 8Переместительные законы сложения и умножения
слагаемых
множителей
От перестановки
Сумма
произведение
Не изменяется
Слайд 10умножение и деление многочлена на число.
Чтобы
многочлен на число,
достаточно на это число
каждый член многочлена и
полученные сложить
Слайд 11Арифметическая и геометрическая прогрессии.
1. Даны последовательности:
3,
5, 7 …
1, 2, 4, 8 …Как построена эта последовательность? Найти следующие три члена последовательности. Что у них общего? И в чем различия?
Как получили число, которое при – Как получили число, на которое
бавляем к предыдущему члену, умножаем предыдущий член,
чтобы получить следующий? Как чтобы получить следующий?
его можно назвать? Как его можно назвать?
Такие последовательности называются
арифметические, геометрические
разность обозначается – d знаменатель обозначается - q
Слайд 122. Определение
Последовательность, каждый член которой начиная со второго, равен
предыдущему,
с одним и тем же числом называется
прогрессией. Число
прогрессии. Таким образам
прогрессия
есть последовательность, заданная рекуррентно
равенством
Слайд 14 3. Свойства
Формула n – го члена
Что надо
знать, чтобы задать прогрессию?
её первый член и разность
а₁ и
d её первый член и знаменатель
в₁ и q
Слайд 15Формула n – го члена для арифметической прогрессии:
а =
а₁+d(n +1)
Формула n –го члена для геометрической прогрессии:
В =
В₁ ∙ qⁿ⁻¹n
n
Слайд 16Характеристическое свойство
Последовательность является
прогрессией тогда, когда любой её
член, начиная со второго, является средним
соседних с ним членов
Слайд 17Свойство прямой и обратной пропорциональностей.
Если две величины
пропорциональны, то отношение двух произвольно взятых
значений одной величиныравно двух соответствующих
значений другой величины
Например: 6:2=3 120:40=3 15:3=100:20
Теги