Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
"Изопериметрическая задача: от глубокой древности до наших дней"
Содержание
- 1. "Изопериметрическая задача: от глубокой древности до наших дней"
- 2. Изопериметрическая задача: от глубокой древности до наших
- 3. Знание – самое превосходное из владений.
- 4. задачиРассмотреть способы решения изопериметрических задач.Выполнить практическое решение изопериметрических задач.Исследовать изопериметрические законы в природе.
- 5. Миф о ДидонеДидона была дочерью царя Тира
- 6. Так была основана цитадель Карфагена Бирсу.
- 7. Задача, которую пришлось решить Дидоне: какая геометрическая
- 8. Задача Дидоны, как самая древняя изопериметрическая задача
- 9. Два случая в задаче Дидоны Береговая
- 10. Береговая линия представляет прямую Отразим симметрично относительно
- 11. При решении задачи воспользуемся теоремой
- 12. Вывод: из всех фигур с данным периметром
- 13. "circumdare"(окружать), "circus" (круг), Можно примерно
- 14. Частный случай задачи Дидоны Береговая линия
- 15. Площадь S= Рассмотрим квадратичную функцию S(x)=
- 16. Другие примеры изопериметрических задач Пример 1. Докажите,
- 17. Задача из школьного курса планиметрии по учебнику А.В.Погорелова
- 18. Зенодор (II в. до н. э.) древнегреческий
- 19. Задачи Зенодора Теорема 1. Из всех многоугольников
- 20. Задачи ЗенодораТеорема 2. Из двух правильных многоугольников
- 21. Задачи ЗенодораТеорема 3. Из всех плоских фигур с равным периметром наибольшую площадь имеет круг.
- 22. Задачи Зенодора Теорема 4. Из двух треугольников
- 23. Исследования такого рода имели не только теоретическое,
- 24. Изопериметрические задачи опытным путём Исследование
- 25. Изопериметрические задачи опытным путём Р = 20см
- 26. Исследование 2 Отмотаем от катушки кусочек нити.
- 27. Диаграмма 1. Площади фигур равного периметра (50
- 28. Из данных фигур равной площади выявить фигуру
- 29. Изопериметрия в жизни Изучив изопериметрические задачи на
- 30. Изопериметрической теореме в пространстве мы склонны верить
- 31. Солнце, Луна, наша Земля, планеты шарообразны или почти шарообразны.
- 32. Немного зная физику поверхностного натяжения,
- 33. То же можно сказать про кота, который
- 34. Рассмотрев эту проблему, можно ответить на вопрос:
- 35. «Всё моё, моё!» — говорит жадный человек,
- 36. Судьба изопериметрической задачи воистину удивительна! Ответ был
- 37. Спасибо за внимание!
- 38. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Научно – практическая конференция «Юные лидеры образования»
МОУ «Гимназия имени
Героя Советского Союза Ю.А. Гарнаева города Балашова Саратовской области»
2016годСлайд 2Изопериметрическая задача: от глубокой древности до наших дней
Работу выполнил:
Путилин Лев,
ученик 10 классаНаучный руководитель: Клушина Н.В., учитель математики высшей категории
Слайд 3 Знание – самое превосходное из владений. Все стремятся к
нему,
само же оно не приходит.
Ал – Бируни
Цель работы:
познакомиться с изопериметрическими задачами на примере задачи Дидоны.
Слайд 4задачи
Рассмотреть способы решения изопериметрических задач.
Выполнить практическое решение изопериметрических задач.
Исследовать
изопериметрические законы в природе.
Слайд 5Миф о Дидоне
Дидона была дочерью царя Тира и женой жреца
Геракла Акербаса, которая вынуждена была бежать с родных мест.
В поисках
новой земли Царице приглянулось одно место на побережье нынешнего Тунисского залива. По условию она могла купить столько земли, сколько можно «окружить бычьей шкурой».
Слайд 6Так была основана цитадель Карфагена Бирсу.
По-гречески «бирсу» как раз
и означает «шкура».
Было это около 825 года до
нашей эры.Слайд 7Задача, которую пришлось решить Дидоне:
какая геометрическая фигура среди фигур
с одинаковым периметром имеет наибольшую площадь?
Или, иначе:
какой формы
должна быть кривая некоторой длины, чтобы площадь фигуры, ограниченная этой кривой была наибольшей? Слайд 8Задача Дидоны,
как самая древняя изопериметрическая задача
Задача Дидоны очень сложная
и относиться к специальному разделу высшей математики, так называемому вариационному
исчислению. Её формулировка даёт классический пример изопериметрической задачи.Слово «изопериметрический» происходит от слов «изос» (по-гречески «равный») и «perimetren» ( по гречески – «обвод, обмер»).
Изопериметрические фигуры - это фигуры, имеющие одинаковый периметр.
Слайд 9Два случая в задаче Дидоны
Береговая линия - произвольная кривая
где
l – длина верёвки,
Г – береговая линия
Этот случай решается
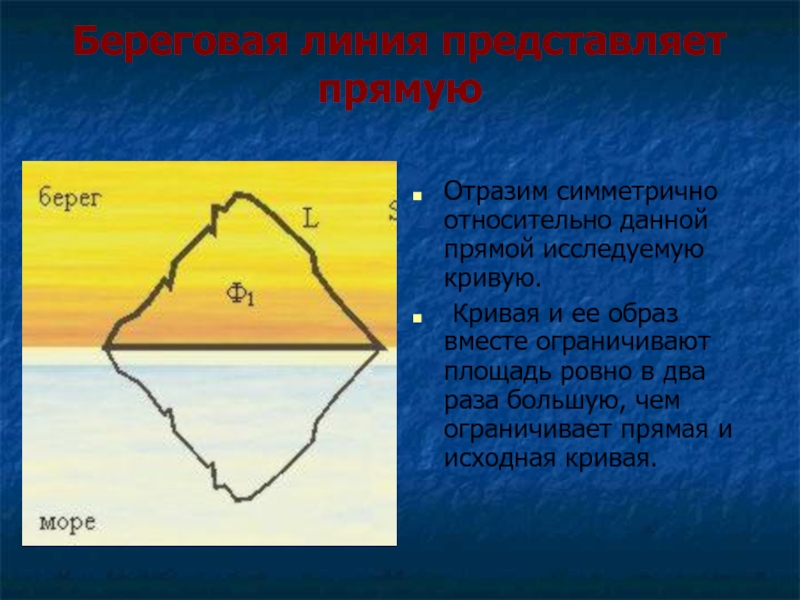
с привлечением понятий и методов математического анализа. А сама задача является задачей на экстремум. Слайд 10Береговая линия представляет прямую
Отразим симметрично относительно данной прямой исследуемую кривую.
Кривая и ее образ вместе ограничивают площадь ровно в два
раза большую, чем ограничивает прямая и исходная кривая.Слайд 11При решении задачи воспользуемся теоремой
(изопериметрическое неравенство)
Если P
- периметр плоской фигуры F,
S – площадь фигуры F, то равенство достигается только в случае круга.
Слайд 12Вывод: из всех фигур с данным периметром наибольшую площадь имеет
круг.
Таким образом, площадь максимальна, когда замкнутая кривая -окружность, для которой
данная прямая является осью симметрии. Следовательно, решение задачи Дидоны является полукруг с центром на берегу моря.
Слайд 13"circumdare"(окружать),
"circus" (круг),
Можно примерно оценить размеры территории, которую по
легенде Дидона могла получить у туземцев.
Представим себе бычью шкуру в
форме прямоугольника размером 1х2 м. разрежем ее на полоски шириной 1мм вдоль длинной стороны.
получается "веревка" длиной примерно 2км.
Так что Дидона могла бы в этом случае отгородить полукруг площадью 0,64
Многие историки считают, что это - первая экстремальная задача, которая обсуждалась в научной литературе
.
Слайд 14Частный случай задачи Дидоны
Береговая линия – прямая,
ограниченный
участок - прямоугольник.
Какой прямоугольник будет иметь наибольшую площадь?
Слайд 15Площадь S=
Рассмотрим квадратичную функцию
S(x)=
,которая принимает наибольшее значение при ,тогда
.Таким образом, наибольшую площадь будет иметь прямоугольник с длинами сторон и .
Слайд 16Другие примеры изопериметрических задач
Пример 1. Докажите, что из всех
треугольников данного периметра наибольшую площадь имеет равносторонний.
Пример 2. Какой из
всех прямоугольников заданного периметра имеет наибольшую площадь?Слайд 18
Зенодор (II в. до н. э.) древнегреческий математик, жил в
Александрии. Он написал целый трактат «О фигурах, имеющих равную периферию».
Хотя трактат Зенодора не сохранился, некоторые его результаты дошли до нас в изложении других математиков, в том числе следующие теоремы.
Слайд 19Задачи Зенодора
Теорема 1. Из всех многоугольников с равным периметром
и равным числом сторон наибольшую площадь имеет правильный многоугольник;
Слайд 20Задачи Зенодора
Теорема 2. Из двух правильных многоугольников с равным периметром
большую площадь имеет тот, у которого число углов больше;
Слайд 21Задачи Зенодора
Теорема 3. Из всех плоских фигур с равным периметром
наибольшую площадь имеет круг.
Слайд 22Задачи Зенодора
Теорема 4. Из двух треугольников с общей стороной
и равными периметрами меньше площадь того, которому принадлежит наибольший из
четырех углов, прилежащих к этой стороне
отсюда сразу следует, что из всех треугольников равного периметра, имеющих общее основание, площадь максимальна у равнобедренного треугольника;
Слайд 23
Исследования такого рода имели не только теоретическое, но и практическое
значение: при разделе земли в древности иногда совершались махинации, связанные
с выдачей участков большого периметра и маленькой площади.Периметр легче измерить, чем площадь, поэтому некоторые доверчивые клиенты судили о величине участка по периметру.
Слайд 24Изопериметрические задачи опытным путём Исследование 1.
Р -18 см
Треугольники
а в с SРазносторонний 3 8 7 √108
5 7 6 √216
4 8 6 √135
Равнобедренный 5 5 8 12
4 7 7 √180
2 8 8 √147
Равносторонний 6 6 6 √243
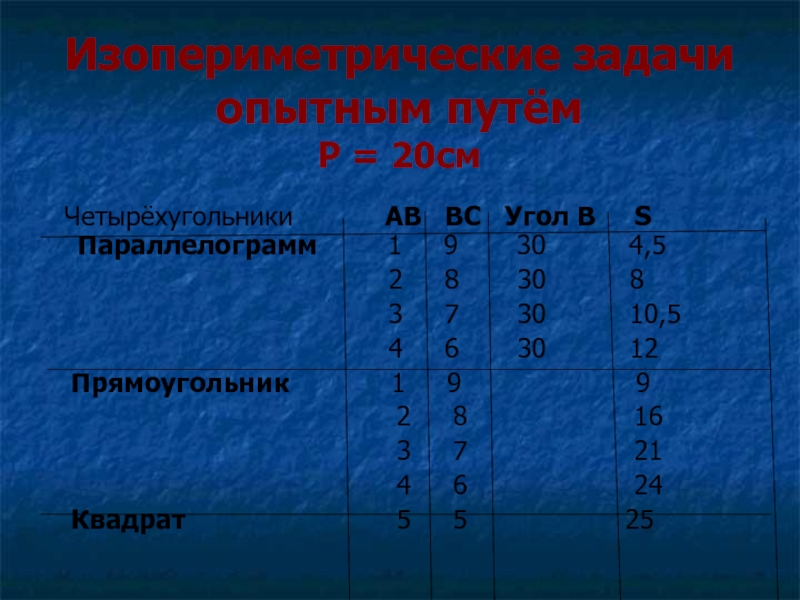
Слайд 25Изопериметрические задачи опытным путём
Р = 20см
Четырёхугольники
АВ ВС Угол В
S Параллелограмм 1 9 30 4,52 8 30 8
3 7 30 10,5
4 6 30 12
Прямоугольник 1 9 9
2 8 16
3 7 21
4 6 24
Квадрат 5 5 25
Слайд 26Исследование 2
Отмотаем от катушки кусочек нити. Отрежем его и свяжем
концами. Положим эту связанную нить на лист бумаги.
Получилась плоская
замкнутая кривая. Выяснить: как следует положить нашу нить, чтобы она охватывала наибольшую площадь?
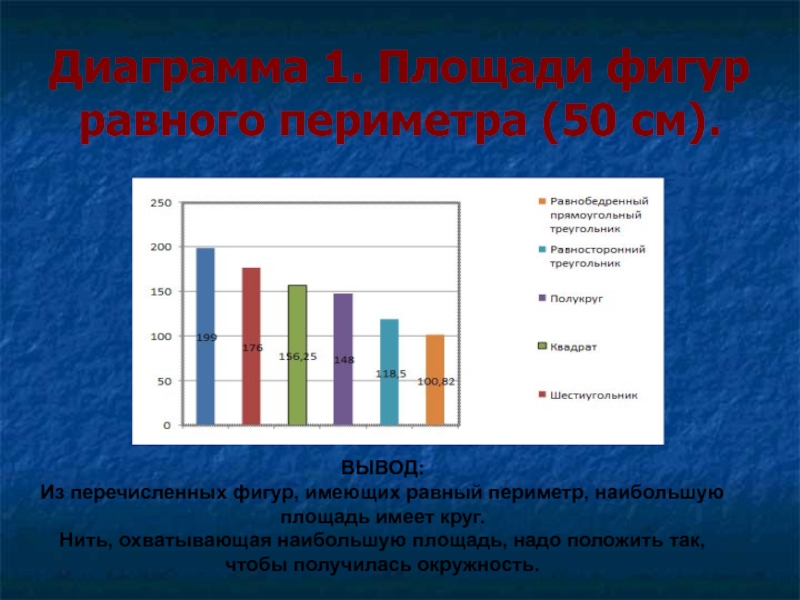
Слайд 27Диаграмма 1. Площади фигур равного периметра (50 см).
ВЫВОД:
Из перечисленных фигур,
имеющих равный периметр, наибольшую площадь имеет круг.
Нить, охватывающая наибольшую площадь,
надо положить так, чтобы получилась окружность.
Слайд 28
Из данных фигур равной площади выявить фигуру с наименьшим периметром.
ВЫВОД:
Из
перечисленных фигур круг, указанный первым, имеет наименьший периметр.
Слайд 29Изопериметрия в жизни
Изучив изопериметрические задачи на плоскости, можно рассмотреть
изопериметрическую теорему в пространстве:
«Из всех тел равного объема наименьшую
поверхность имеет шар». Слайд 30Изопериметрической теореме в пространстве мы склонны верить без математического доказательства.
Сама природа расположена в пользу шара. Дождевые капли, мыльные пузыри
шарообразны.
Слайд 32
Немного зная физику поверхностного натяжения, можно научиться изопериметрической
теореме у мыльного пузыря. Будучи сжаты окружающей средой, они стремятся
в силу сцепления образовать при неизменном объеме более толстую поверхностную пленку.
Слайд 33
То же можно сказать про кота, который в холодную ночь
сворачивается в клубочек и таким образом делает своё тело насколько
возможно шарообразным.Пытаясь сохранить тепло, он уменьшает свою поверхность. Таким образом, он решает задачу о теле с данным объемом и наименьшей поверхностью.
Слайд 34Рассмотрев эту проблему, можно ответить на вопрос: почему нефтехранилища на
крупных заводах всегда делаются цилиндрическими (а иногда даже шарообразными), а
не в виде, скажем, куба, что технологически было бы гораздо удобнее?
Слайд 35
«Всё моё, моё!» — говорит жадный человек, собирая свои руки
в круг, показывая, как много добра он может ими захватить.
При этом не подозревая, что демонстрирует решение одной из самых древних задач математики — изопериметрической задачи.Слайд 36Судьба изопериметрической задачи воистину удивительна! Ответ был известен человечеству почти
3000 лет и ни у кого не вызывал сомнений, но
строго доказать его удалось лишь в конце XIX века.Якоб Штейнер
Леонард Эйлер
Якоб Бернулли