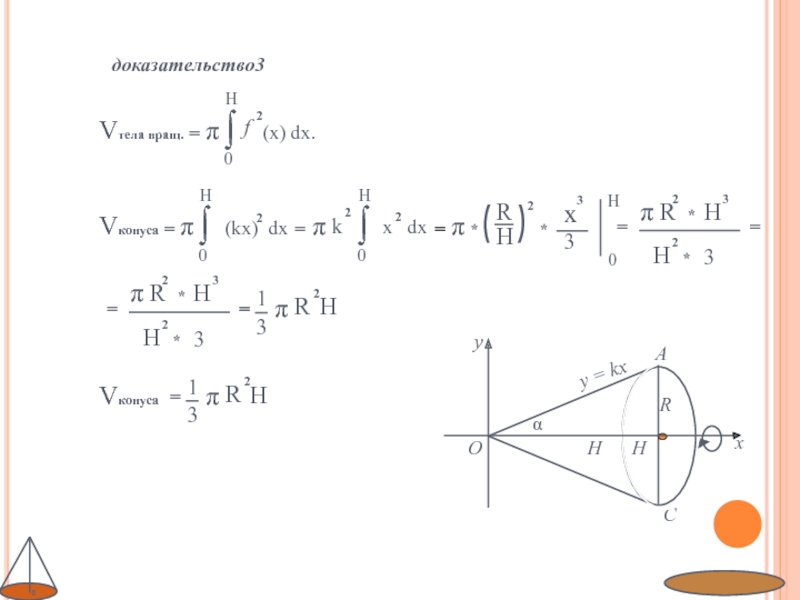Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Компьютерная поддержка по теме "Тела вращения на примере конуса"
Содержание
- 1. Компьютерная поддержка по теме "Тела вращения на примере конуса"
- 2. Конус в переводе с греческого «konos» означает
- 3. Большой трактат о конических сечениях был написан
- 4. понятие конуса элементы конуса конус вращения площадь
- 5. Понятие конуса Определение: тело, ограниченное конической поверхностью и кругом с границей L, называется конусом.
- 6. боковая (коническая) поверхностьвысота конуса (РО)ось конусавершина конуса (Р)основание конусарадиус конуса (r)Элементы конуса BrобразующиеP
- 7. Прямой круговой конус является объединением всех равных
- 8. Сечение, перпендикулярное к оси конуса
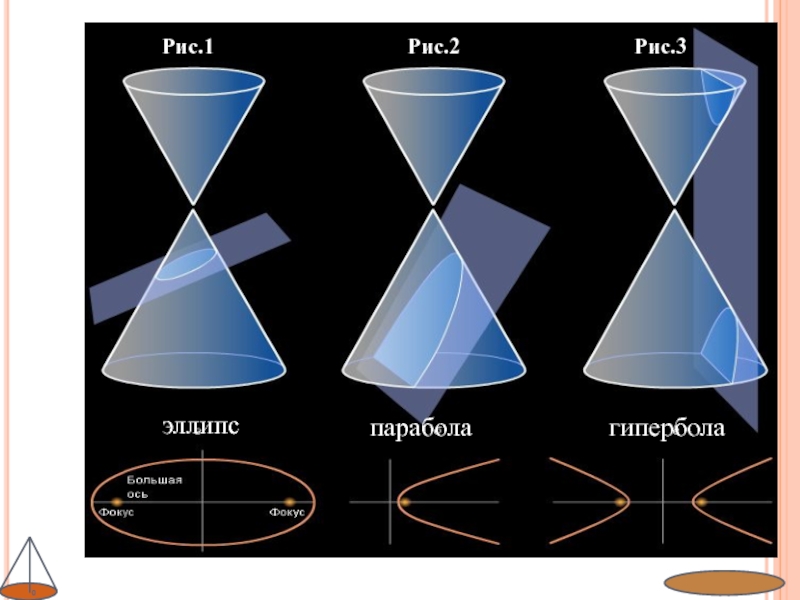
- 9. Рис.1Рис.2Рис.3эллипспараболагипербола
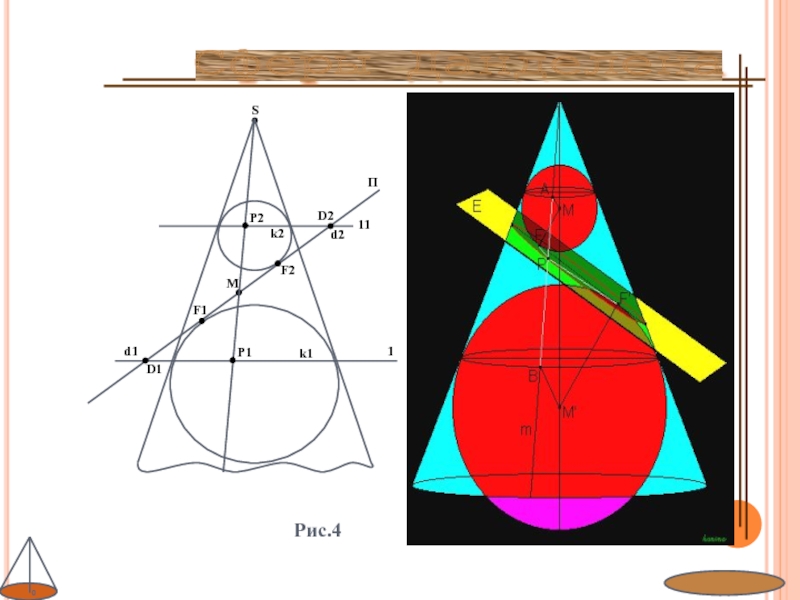
- 10. Рис.4Сферы Данделена
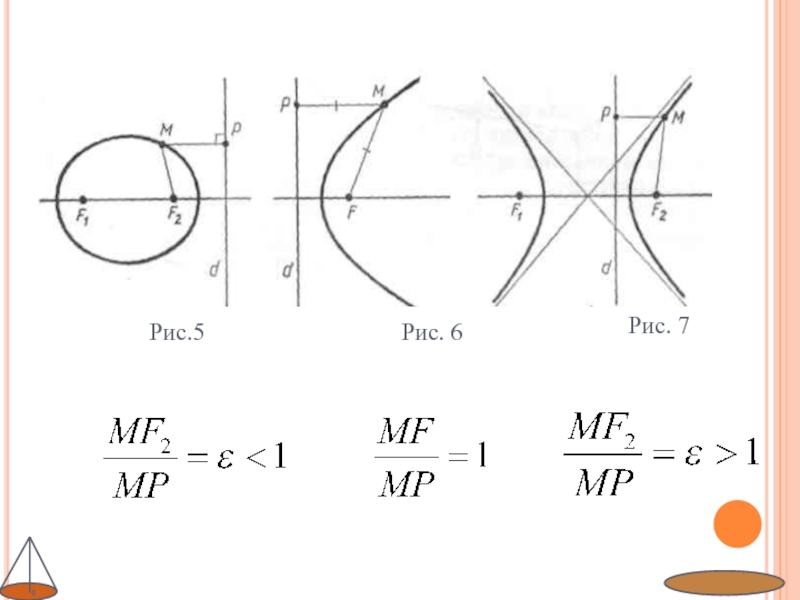
- 11. Рис.5Рис. 6Рис. 7
- 12. Применение свойств конических сечений
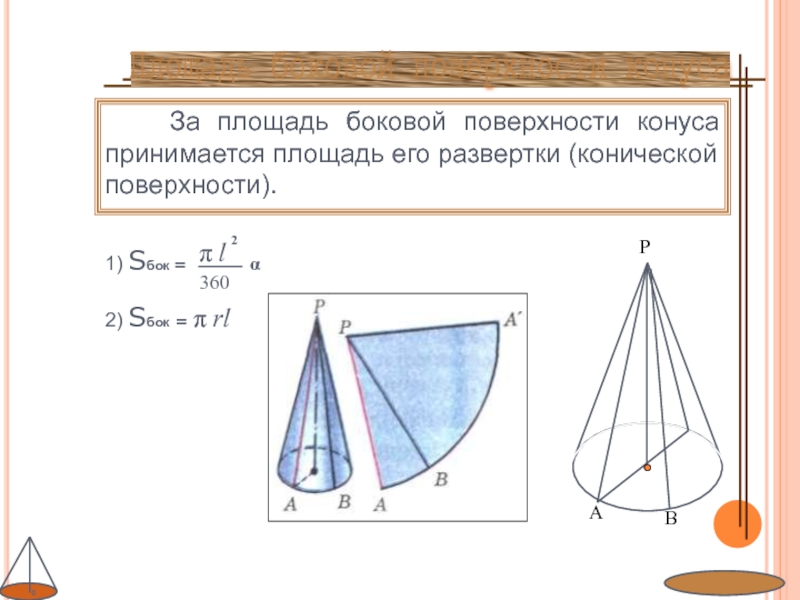
- 13. За площадь боковой поверхности конуса
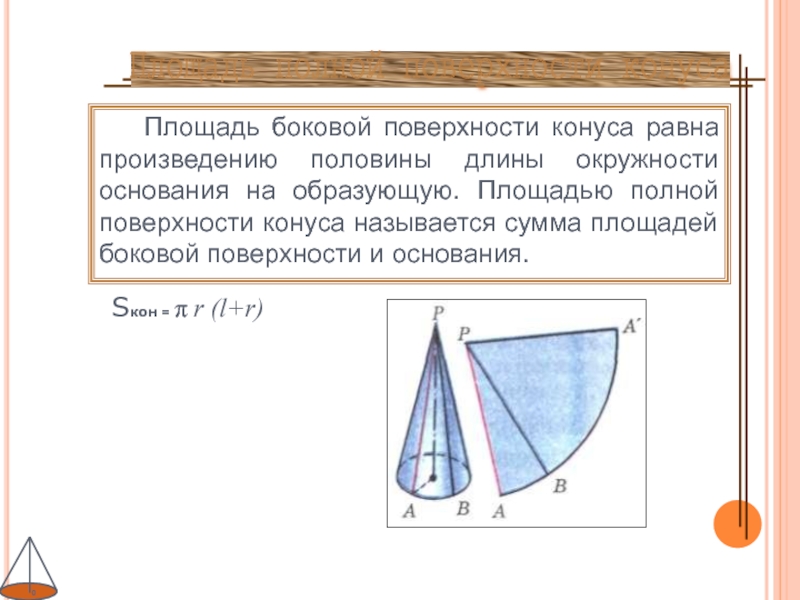
- 14. Площадь полной поверхности конуса Площадь
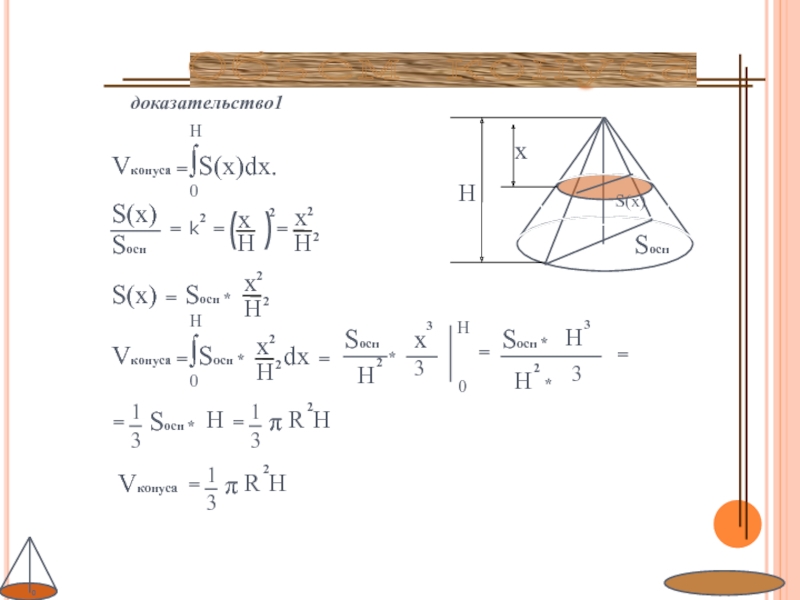
- 15. доказательство1Обьем конуса Vконуса
- 16. доказательство2За величину объема конуса принимается предел, к
- 17. доказательство3
- 18. Решение задач по теме конус Задача 1.
- 19. Задача 2. (объем конуса)Авиационная бомба среднего калибра
- 20. Задача 3. (Объем конуса)Смолу для промышленных нужд
- 21. Задача 4. (Объем конуса)«... Читал я где-то,
- 22. Войско в 100 000 воинов считалось очень внушительным.V
- 23. 1. Александров А. Д., Вернер А. Л.,
- 24. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Автор работы:
Игнатенко Татьяна Петровна
МБОУ «Эсто-Алтайская СОШ им.Д.Н.Кугультинова»
Учитель математики
2014г
Компьютерная
поддержка по теме
Слайд 2Конус в переводе с греческого «konos» означает «сосновая шишка».
С
конусом люди знакомы с глубокой древности.
Много сделала для геометрии
школа Платона (428–348 гг. до н. э.). Школе Платона, в частности, принадлежит: а) исследование свойств призмы, пирамиды, цилиндра и конуса;
б) изучение конических сечений.
Историческая справка о конусе
Слайд 3Большой трактат о конических сечениях был написан Аполлонием Пергским– учеником
Евклида, который создал великий труд из 15 книг под названием
«Начала». Эти книги издаются и по сей день, а в школах Англии по ним учатся до сих пор.Историческая справка о конусе
Слайд 4
понятие конуса
элементы конуса
конус вращения
площадь полной поверхности конуса
площадь боковой поверхности конуса
объем конуса
решение задач по теме
конус усеченный конус
конические сечения
сферы Данделена
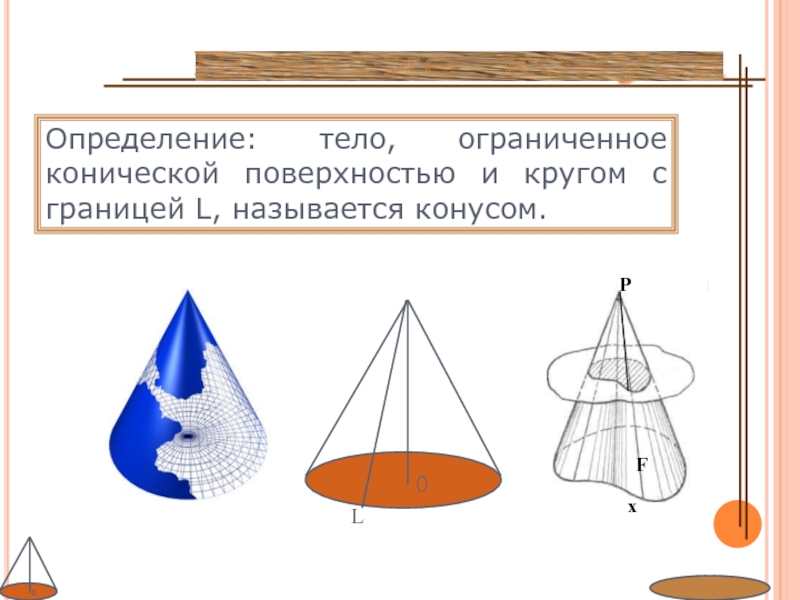
Слайд 5Понятие конуса
Определение: тело, ограниченное конической поверхностью и кругом с
границей L, называется конусом.
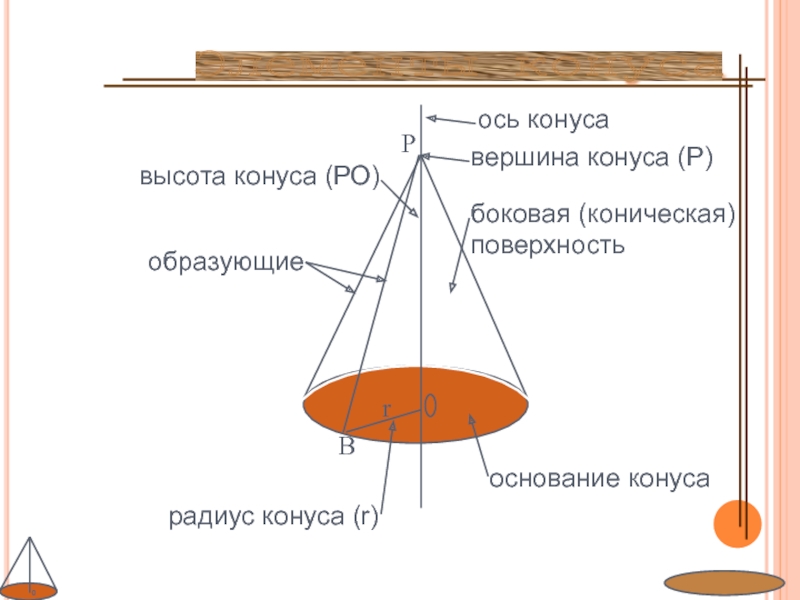
Слайд 6боковая (коническая) поверхность
высота конуса (РО)
ось конуса
вершина конуса (Р)
основание конуса
радиус конуса
(r)
Элементы конуса
B
r
образующие
P
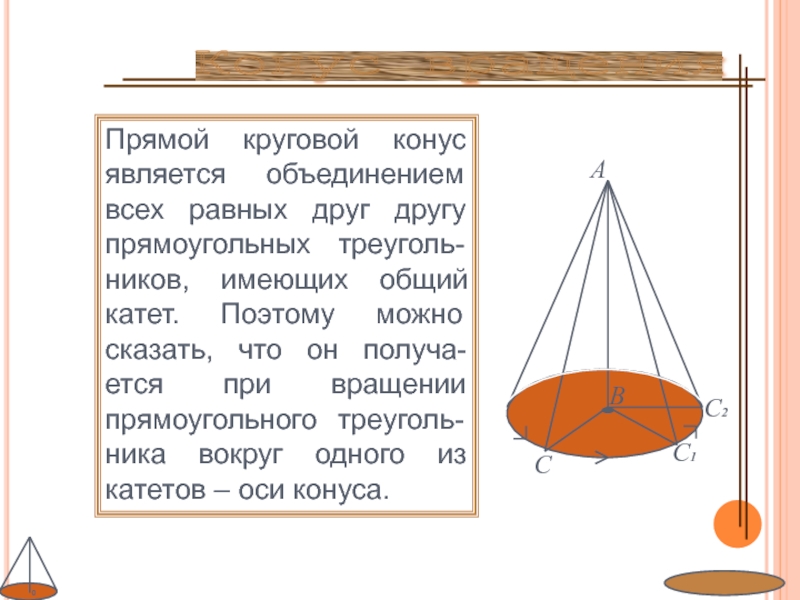
Слайд 7Прямой круговой конус является объединением всех равных друг другу прямоугольных
треуголь-ников, имеющих общий катет. Поэтому можно сказать, что он получа-ется
при вращении прямоугольного треуголь-ника вокруг одного из катетов – оси конуса.Конус вращения
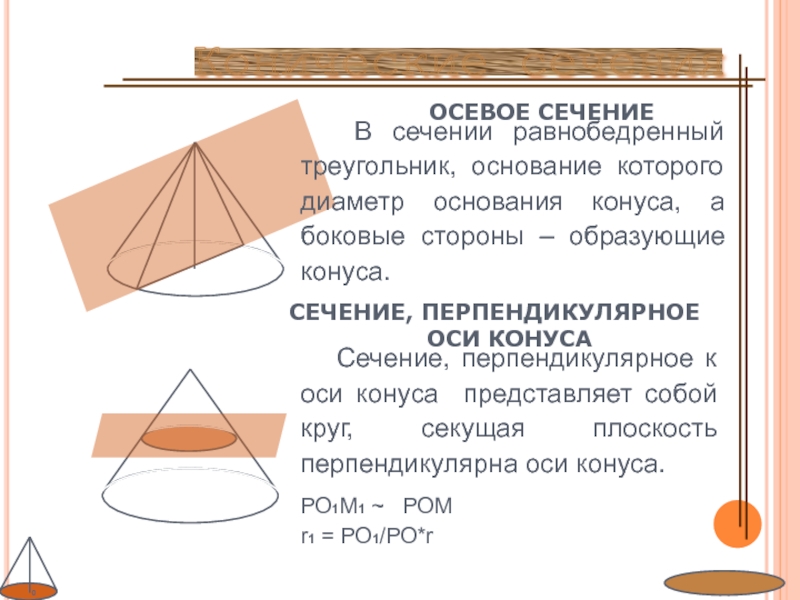
Слайд 8 Сечение, перпендикулярное к оси конуса представляет собой круг,
секущая плоскость перпендикулярна оси конуса.
РО1М1 ~ РОМ
r1 = РО1/РО*r
ОСЕВОЕ
СЕЧЕНИЕКонические сечения
СЕЧЕНИЕ, ПЕРПЕНДИКУЛЯРНОЕ ОСИ КОНУСА
В сечении равнобедренный треугольник, основание которого диаметр основания конуса, а боковые стороны – образующие конуса.
Слайд 13 За площадь боковой поверхности конуса принимается площадь его
развертки (конической поверхности).
1) Sбок =
Площадь боковой поверхности конуса
Слайд 14Площадь полной поверхности конуса
Площадь боковой поверхности конуса
равна произведению половины длины окружности основания на образующую. Площадью полной
поверхности конуса называется сумма площадей боковой поверхности и основания.Слайд 16доказательство2
За величину объема конуса принимается предел, к которому стремится объем
правильной пирамиды, вписанной в конус, при неограниченном удвоении числа сторон
ее основания.Слайд 18Решение задач по теме конус
Задача 1.
Высота конуса равна
диаметру его основания. Найти отношение площади его основания к площади
боковой поверхности.Решение:
Пусть радиус основания конуса равен R, тогда площадь основания Sосн = R , а высота конуса 2R.
2
π
Слайд 19Задача 2. (объем конуса)
Авиационная бомба среднего калибра дает при взрыве
воронку диаметром 6 м и глубиной 2 м. Какое количество земли (по
массе) выбрасывает эта бомба, если 1 м3 земли имеет массу 1650 кг?Решение:
* 3 * 2 =6 (м )
2
3
π
Ответ: P = 31 т.
Слайд 20Задача 3. (Объем конуса)
Смолу для промышленных нужд собирают, подвешивая конические
воронки к соснам. Сколько воронок диаметром 10 см с образующей 13 см
нужно собрать, чтобы заполнить 10-литровое ведро?Дано: Решение.
коническая воронка
D = 10 см
L = 13 см
V – ?
Слайд 21Задача 4. (Объем конуса)
«... Читал я где-то, что царь однажды
воинам своим велел снести земли по горсти в кучу. И
гордый холм возвысился, и царь мог с высоты с весельем озирать и дол, покрытый белыми шатрами, и море, где бежали корабли.»А.С. Пушкин «Скупой рыцарь»
Это одна из немногих легенд, в которой при кажущемся правдоподобии нет и зерна правды. Докажите геометрически, что если бы какой-нибудь древний деспот вздумал осуществить такую затею, он был бы обескуражен мизерностью результата. Перед ним высилась бы настолько жалкая куча земли, что никакая фантазия не смогла бы раздуть ее в легендарный «гордый холм».
Слайд 22Войско в 100 000 воинов считалось очень внушительным.
V = 0,2*100 000 =
20 000 дм3 = 20 м3.
Угол откоса Ј 45°, иначе земля начнет осыпаться.
Возьмем
угол откоса наибольшим возможным, т. е. 45° Дано: конус
V = 20 м3
a = 45°
Найти: H конуса
Решение:
Так как H = R, то:
Слайд 23
1. Александров А. Д., Вернер А. Л., Рыжик В. И.
/ Геометрия для 10-11 классов: Учебное пособие для учащихся школ
и классов с углубленным изучением математики – 3-е издание, перераб. – М.: Просвещение, 1992. – 464с.2. Геометрия 10-11: учеб. для общеобразоват. учреждений / Атанасян Л. С., Бутузов В.Ф., Кадомцев и др. – 14-е изд. – М.: Просвещение,2005. – 206с.
3. Крамор В. С. / Повторяем и систематизируем школьный курс геометрии. – 3-е изд., испр. И доп. – М.:Мнемозина, 2004. – 336 с.
4. Смирнова И. М. / Геометрия: Учебное пособие для 10-11 классов гуманит. Профиля. – М.: Просвещение, 1997. – 159 с.
5. Математика. – репринтное издание «Математического энциклопедического словаря» 1988 г.- М.: Большая Российская энциклопедия, 2003. - с.
6. http://ru.wikipedia.org/wiki/
Список источников основного содержания: