Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация к уроку геометрии в 7 классе по теме "Свойства параллельных прямых"
Содержание
- 1. Презентация к уроку геометрии в 7 классе по теме "Свойства параллельных прямых"
- 2. ЦЕЛЬ УРОКА: Рассмотреть свойства параллельных прямых.ЗАДАЧИ
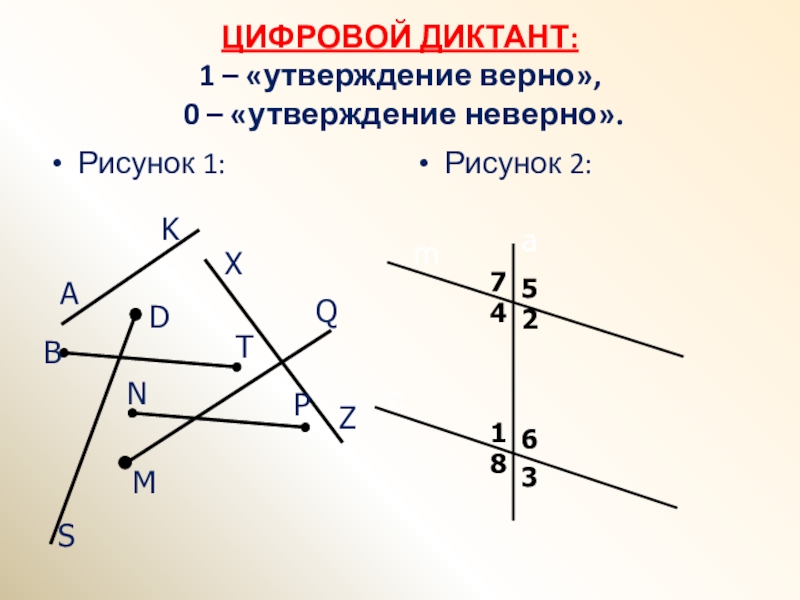
- 3. ЦИФРОВОЙ ДИКТАНТ: 1 – «утверждение верно», 0 – «утверждение неверно».Рисунок 1:Рисунок 2:amc
- 4. ПРОВЕРКА:1 вариант:2 вариант:Критерии оценивания:«5» – нет ошибок.«4»
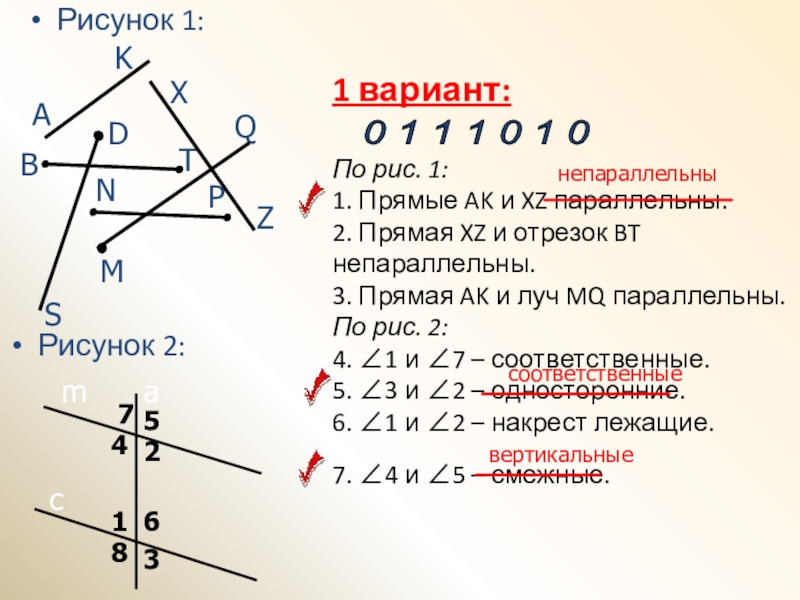
- 5. 1 вариант: По рис. 1:
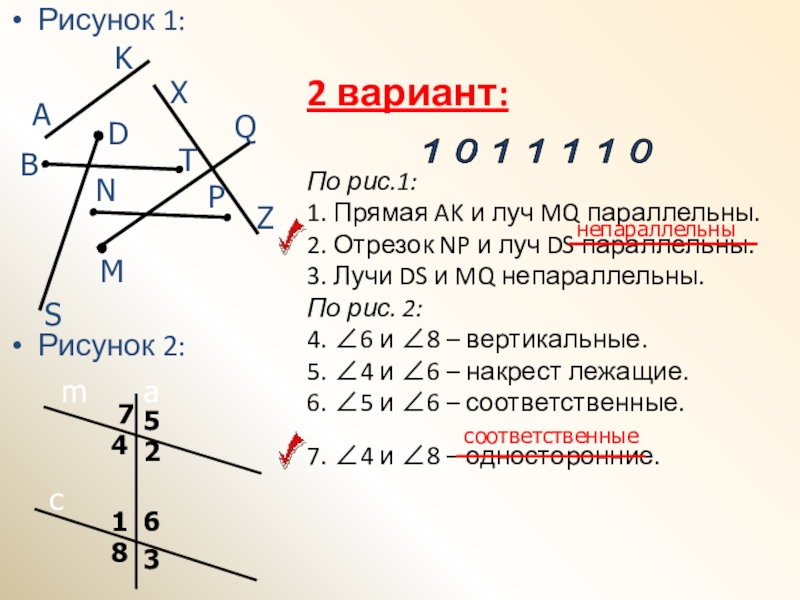
- 6. 2 вариант: По рис.1: 1.
- 7. ТестРаздаточный материал, № 2Ответы к тестуСледует вычеркнуть слова: очевидно, принятые, объяснений, обоснований;а;а, б;б, в, е, ж;б;в.
- 8. Ответы к тесту1) Вычеркнуть лишние слова в
- 9. 4) Указать следствия аксиомы параллельных прямых.а) Если
- 10. 5) Указать правильный ответ на вопрос.Если через
- 11. Решить задачуа) Доказать: АВ ׀׀ СDа)б)
- 12. Вывод:Если две параллельные прямые пересечены третьей,то накрест лежащие углы равны.
- 13. Если при пересечении двух прямых секущей накрест
- 14. Следствие: Если прямая перпендикулярна к одной из двух параллельных прямых, то она перпендикулярна и к другой.
- 15. Если при пересечении двух прямых секущей соответственные
- 16. Решите задачиЗадача № 1Задача № 2Решить задачи из раздаточного материала
- 17. Домашнее задание:§ 29Решить задачи по готовым чертежам
- 18. ВЫБЕРИ СВОЕГО СМАЙЛИКА:МНЕ БЫЛО ЛЕГКО РАБОТАТЬ НА
- 19. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2ЦЕЛЬ УРОКА:
Рассмотреть свойства параллельных прямых.
ЗАДАЧИ УРОКА:
научить учащихся применять свойства
параллельных прямых; закрепить знания, умения, навыки учащихся по теме «Аксиома
параллельных прямых».развивать умение сравнивать, анализировать, обобщать, делать вывод, осуществлять перенос знаний и умений в новой нестандартной ситуации;
воспитывать сознательное отношение к труду, расширять кругозор учащихся.
Слайд 4ПРОВЕРКА:
1 вариант:
2 вариант:
Критерии оценивания:
«5» – нет ошибок.
«4» – 1 ошибка.
«3»
– 2-3 ошибки.
«2» – более 3-х ошибок.
0 1 1 1
0 1 0 1 0 1 1 1 1 0
Слайд 51 вариант: По рис. 1: 1. Прямые AK и XZ параллельны. 2.
Прямая XZ и отрезок BT непараллельны. 3. Прямая AK и луч
MQ параллельны. По рис. 2: 4. ∠1 и ∠7 – соответственные. 5. ∠3 и ∠2 – односторонние. 6. ∠1 и ∠2 – накрест лежащие. 7. ∠4 и ∠5 – смежные.Рисунок 1:
Рисунок 2:
0 1 1 1 0 1 0
непараллельны
вертикальные
соответственные
Слайд 62 вариант: По рис.1: 1. Прямая AK и луч MQ параллельны. 2.
Отрезок NP и луч DS параллельны. 3. Лучи DS и MQ
непараллельны. По рис. 2: 4. ∠6 и ∠8 – вертикальные. 5. ∠4 и ∠6 – накрест лежащие. 6. ∠5 и ∠6 – соответственные. 7. ∠4 и ∠8 – односторонние.Рисунок 1:
Рисунок 2:
непараллельны
соответственные
1 0 1 1 1 1 0
Слайд 7Тест
Раздаточный материал, № 2
Ответы к тесту
Следует вычеркнуть слова: очевидно, принятые,
объяснений, обоснований;
а;
а, б;
б, в, е, ж;
б;
в.
Слайд 8Ответы к тесту
1) Вычеркнуть лишние слова в скобках:
Аксиома – это
(очевидные, принятые, исходные) положения геометрии,
не требующие (объяснений, доказательств, обоснований).
2)
Выбрать окончание формулировки аксиомы параллельных прямых:Через точку, не лежащую на данной прямой, проходит:
а) только одна прямая, параллельная данной;
б) всегда проходит прямая, параллельная данной;
в) только одна прямая, не пересекающаяся с данной.
3) Что может быть следствием аксиомы или теоремы? Указать неверные ответы.
а) Утверждение, не требующее доказательства.
б) Новая теорема, для доказательства которой использована аксиома
или теорема.
в) Утверждение, непосредственно выводимое из аксиомы или теоремы.
Слайд 94) Указать следствия аксиомы параллельных прямых.
а) Если отрезок или луч
пересекает одну из параллельных прямых,
то он пересекает и
другую.б) Если две прямые параллельны третьей прямой,
то они параллельны друг другу.
в) Если прямая пересекает одну из параллельных прямых,
то она пересекает и другую.
г) Если три прямые параллельны,
то любые две из них параллельны друг другу.
д) Если две прямые не параллельны третьей прямой,
то они не параллельны между собой.
е) Если прямая пересекает одну из параллельных прямых,
то она не может не пересекать другую.
ж) Если две прямые параллельны третьей прямой,
то они не могут быть не параллельны между собой.
Слайд 105) Указать правильный ответ на вопрос.
Если через точку, лежащую вне
прямой, проведено несколько прямых, то сколько из них пересекаются с
исходной прямой?а) Неизвестно, так как не показано, сколько прямых проведено
через точку.
б) Все, кроме параллельной прямой.
в) Все, которые имеют на рисунке точку пересечения с исходной прямой.
6) Почему, если одна из прямых, проходящих через точку, лежащую вне заданной прямой, параллельна этой прямой, то другие прямые, проходящие через эту точку, не могут быть ей параллельны? Указать неправильный ответ на этот вопрос.
а) Это противоречит аксиоме параллельных прямых.
б) Любая другая прямая, если она также параллельна заданной,
совпадает с первой.
в) Все другие прямые имеют точку пересечения с заданной прямой,
хотя она может находиться на сколь угодно большом расстоянии
от исходной точки.
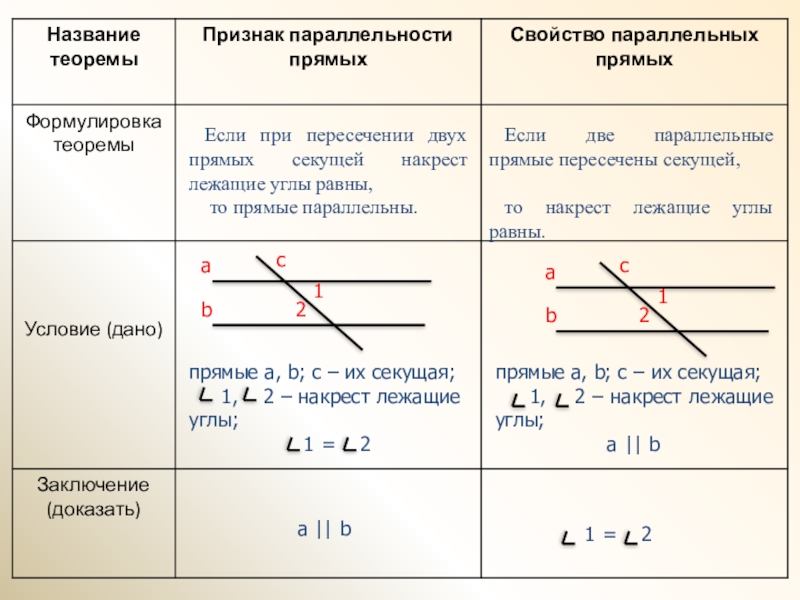
Слайд 13Если при пересечении двух прямых секущей накрест лежащие углы равны,
то прямые параллельны.
а || b
Если две параллельные прямые пересечены секущей,
то накрест лежащие углы равны.
Слайд 14Следствие: Если прямая перпендикулярна к одной из двух параллельных прямых,
то она перпендикулярна и к другой.
Слайд 15Если при пересечении двух прямых секущей соответственные углы равны,
то
прямые параллельны.
Если при пересечении двух прямых секущей сумма односторонних углов
равна 1800,то прямые параллельны.
Если две параллельные прямые пересечены секущей,
то соответственные углы равны.
Если две параллельные прямые пересечены секущей,
то сумма односторонних углов равна 1800.