Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математические софизмы, парадоксы 10 класс
Содержание
- 1. Математические софизмы, парадоксы 10 класс
- 2. Цель: рассмотреть основные виды математических софизмов и
- 3. Математический софизм – удивительное утверждение, в доказательстве
- 4. Парадокс (греч. "пара" - "против", "докса" -
- 5. арифметическиегеометрическиеалгебраическиеВ своей работе я рассмотреламного математических софизмови сейчас приведу примерынекоторых из них.
- 6. Алгебраические софизмы. Алгебра — один из
- 7. «Два неодинаковых натуральных числа равны между
- 8. «Уравнение x-a=0 не имеет корней» Дано
- 9. Арифметика - (греч. arithmetika, от arithmys
- 10. «Дважды два - пять» Напишем
- 11. «Пять равно шести»
- 12. Геометрические софизмы
- 13. Задача о треугольникеДан прямоугольный
- 14. Разгадка простая: первый треугольник немного "вогнут",
- 15. ЭКСПЕРИМЕНТАЛЬНЫЕ ИССЛЕДОВАНИЯ ПО ВОСПРИЯТИЮ
- 16. В рамках данного исследования ученикам 8 «А»
- 17. 5. Крокодил украл ребенка; он обещал отцу вернуть
- 18. Проанализировав ответы на вопросы, мы получили следующие
- 19. 2
- 20. 3 вопрос: Возьмём числовое
- 21. 4 вопрос: Дано уравнение x-a=0. Разделив обе
- 22. 5 вопрос: Крокодил украл ребенка; он
- 23. 6 вопрос: Одному деревенскому брадобрею приказали «брить
- 24. 7 вопрос: Человек произносит: «Я лгу». Он
- 25. 8 вопрос: Что будет, если Буратино скажет:
- 26. ЗаключениеО математических софизмах и парадоксах можно говорить
- 27. Спасибо за внимание !
- 28. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Математические софизмы,
парадоксы
МКОУ СОШ им. Х.К. Табухова, с.п. Анзорей
Руководитель проекта:
Арахова Марита
Барасбиевна
Слайд 2Цель: рассмотреть основные виды математических софизмов и парадоксов, причины их
возникновения и восприятие учениками.
Задачи:
Познакомиться с софизмами и парадоксами
Изучить историю
возникновения и их видыНаучиться распознавать ошибки в них
Провести исследование, в ходе которого можно будет определить процент объективности восприятия софизмов и парадоксов учащимися МКОУ СОШ им. Х.К.Табухова.
Сделать вывод по результатам проведенной работы.
Слайд 3Математический софизм – удивительное утверждение, в доказательстве которого кроются незаметные,
а подчас и довольно тонкие ошибки.
Особенно часто в софизмах
выполняют "запрещенные" действия или не учитываются условия применимости теорем, формул и правил. Математические софизмы
Софизм- формально кажущееся правильным, но по существу ложное умозаключение, основанное на неправильном подборе исходных положений
Слайд 4 Парадокс (греч. "пара" - "против", "докса" - "мнение") близок к
софизму. Но от него он отличается тем, что это не
преднамеренно полученный противоречивый результат.Парадокс - странное, расходящееся с общепринятым мнением, высказывание, а также мнение, противоречащее (иногда только на первый взгляд) здравому смыслу.
Математический парадокс – высказывание, которое может быть доказано и как истинна, и как ложь.
Парадоксы
Слайд 5арифметические
геометрические
алгебраические
В своей работе я рассмотрела
много математических софизмов
и сейчас приведу примеры
некоторых
из них.
Слайд 6Алгебраические софизмы.
Алгебра — один из больших разделов
математики, принадлежащий наряду с арифметикой и геометрией к числу старейших
ветвей этой науки. Алгебраические софизмы – намеренно скрытые ошибки в уравнениях и числовых выражениях.Слайд 7 «Два неодинаковых натуральных числа равны между собой»
решим систему двух
уравнений
Сделаем это подстановкой у из 2-го уравнения в 1, получаем х+8-х=6, откуда 8=6
Где ошибка
Уравнение (2) можно записать как х+2у=8, так что исходная система запишется в виде:
Х+2у=6, Х+2у=8
В этой системе уравнений коэффициенты при переменных одинаковы, а правые части не равны между собой, из этого следует, что система несовместна, т.е. не имеет ни одного решения. Графически это означает, что прямые
у=3-х/2 и у=4-х/2 параллельны и не совпадают.
Перед тем, как решать систему линейных уравнений, полезно проанализировать, имеет ли система единственное решение, бесконечно много решений или не имеет решений вообще.
Слайд 8«Уравнение x-a=0 не имеет корней»
Дано уравнение x-a=0. Разделив
обе части этого уравнения на x-a, получим, что 1=0. Поскольку
это равенство неверное, то это означает, что исходное уравнение не имеет корней.Где ошибка?
Поскольку x=a – корень уравнения, то, разделив на выражение x-a обе его части, мы потеряли этот корень и поэтому получили неверное равенство 1=0.
Слайд 9 Арифметика - (греч. arithmetika, от arithmys — число), наука
о числах, в первую очередь о натуральных (целых положительных) числах
и (рациональных) дробях, и действиях над ними. Так что же такое арифметические софизмы?Арифметические софизмы – это числовые выражения, имеющие неточность или ошибку, не заметную с первого взгляда.
Слайд 10 «Дважды два - пять»
Напишем тождество 4:4=5:5.
Вынесем из каждой части тождества общие
множители за скобки, получаем:
4(1:1)=5(1:1) или Так как 1:1=1, то сократим и получим
Где ошибка?
Ошибка сделана при вынесении общих множителей 4 из левой части и 5 из правой. Действительно, 4:4=1:1, но 4:4≠4(1:1).
Слайд 11 «Пять равно шести»
Возьмем тождество
35+10-45=42+12-54.
В каждой части вынесем за скобки общий множитель:
5(7+2-9)=6(7+2-9).
Теперь, получим, что 5=6.
Где ошибка?
Ошибка допущена при делении верного равенства 5(7+2-9)=6(7+2-9) на число
7+2-9, равное 0. Этого нельзя делать.
Любое равенство можно делить только на число, отличное от 0.
Слайд 12Геометрические софизмы
Это
умозаключения или рассуждения, обосновывающие какую-нибудь заведомую нелепость, абсурд или противоречивое
утверждение, связанное с геометрическими фигурами и действиями над нимиСлайд 13 Задача о треугольнике
Дан прямоугольный треугольник 13×5 клеток,
составленный из 4 частей. После перестановки частей при визуальном сохранении
изначальных пропорций появляется дополнительная, не занятая ни одной частью, клетка. Как такое возможно?Слайд 14
Разгадка простая: первый треугольник немного "вогнут", а второй -
слегка выпуклый. В этом можно убедиться, сравнив наклон гипотенузы синего
и жёлтого кусочков: у жёлтого наклон = 0.375, а у синего - 0.4. Получается, что общие площади верхнего и нижнего треугольников всё-таки различаются, а разница как раз составляет одну клетку!Слайд 15 ЭКСПЕРИМЕНТАЛЬНЫЕ ИССЛЕДОВАНИЯ ПО ВОСПРИЯТИЮ СОФИЗМОВ И ПАРАДОКСОВ УЧЕНИКАМИ МКОУ СОШ
ИМ. Х.К.ТАБУХОВА С.П. АНЗОРЕЙ 1. Сравнение восприятия логических софизмов и
парадоксов учениками 8 и 10 классовСлайд 16В рамках данного исследования ученикам 8 «А» и 10 «А»
классов (n=42) были предоставлены идентичные вопросники, включающие 8 вопросов: 1. Знакомо ли
Вам понятие «софизм»? (Да/Нет) 2. Знакомо ли Вам понятие «парадокс»? (Да/Нет) 3. Возьмём числовое равенство: 35+10-45=42+12-54. Вынесем общие множители левой и правой частей за скобки. Получим: 5(7+2-9)=6(7+2-9). Разделим обе части этого равенства на общий множитель (заключенный в скобки). Получаем 5=6. Как Вы это объясните? (Ошибки нет/ Допущена ошибка в условии/ Допущена ошибка в решении (указать ошибку)) 4. Дано уравнение x-a=0. Разделив обе части этого уравнения на x-a, получим, что 1=0. Поскольку это равенство неверное, то это означает, что исходное уравнение не имеет корней. Допущена ли здесь ошибка, и если да, то какая? (Ошибки нет/ Допущена ошибка в условии/ Допущена ошибка в решении (указать ошибку))Слайд 175. Крокодил украл ребенка; он обещал отцу вернуть ребенка, если отец
угадает – вернет ему крокодил ребенка или нет. Что должен
сделать крокодил, если отец скажет, что крокодил не вернет ему ребенка? (Вернуть/Не возвращать/Решить невозможно) 6. Одному деревенскому брадобрею приказали «брить всякого, кто сам не бреется, и не брить того, кто сам бреется». Как он должен поступить с самим собой? (Брить/ Не брить/ Решить невозможно) 7. Человек произносит: «Я лгу». Он обманывает или говорит правду? (Говорит правду/ Лжет/ Решить невозможно). 8. Что будет, если Буратино скажет "У меня сейчас вырастет нос"? (Нос вырастет/Не вырастет/Решить невозможно).Слайд 18Проанализировав ответы на вопросы, мы получили следующие результаты:
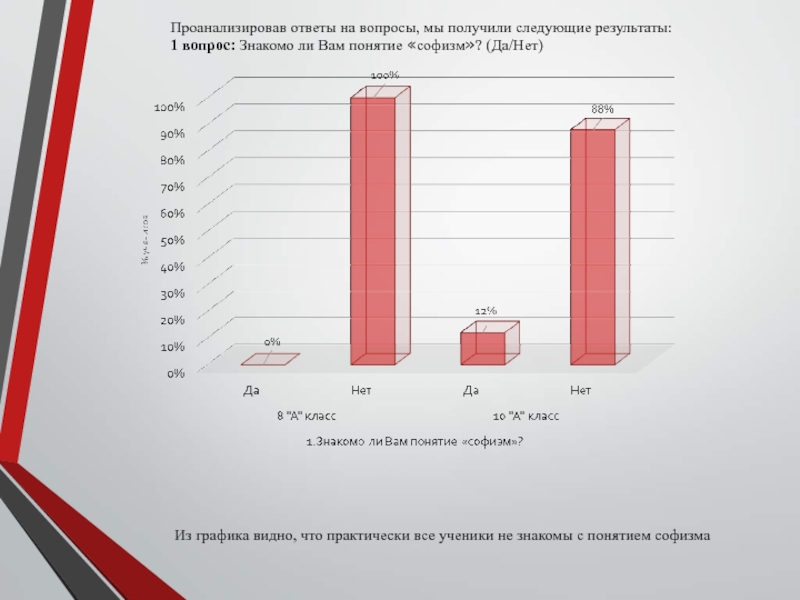
1 вопрос: Знакомо
ли Вам понятие «софизм»? (Да/Нет)
Из графика видно, что практически все
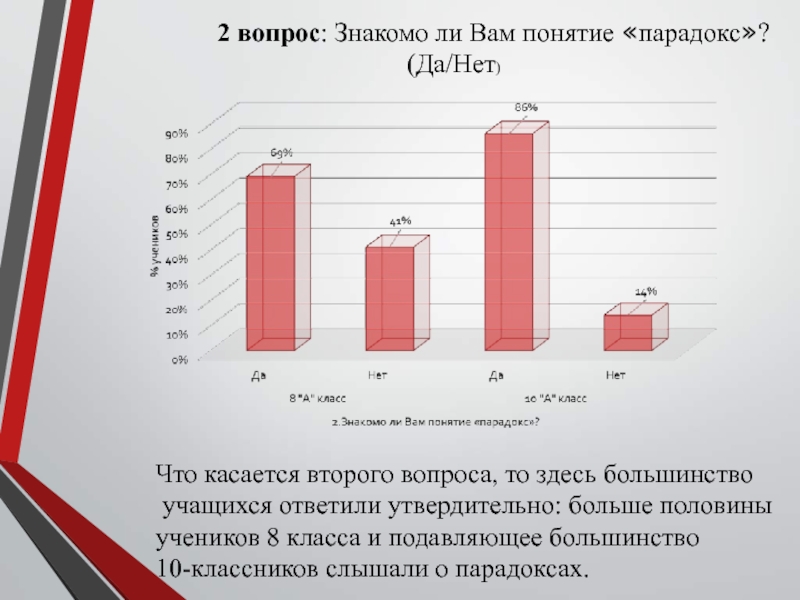
ученики не знакомы с понятием софизмаСлайд 19 2 вопрос: Знакомо ли
Вам понятие «парадокс»? (Да/Нет)
Что касается второго вопроса, то здесь большинство
учащихся ответили утвердительно: больше половины учеников 8 класса и подавляющее большинство
10-классников слышали о парадоксах.
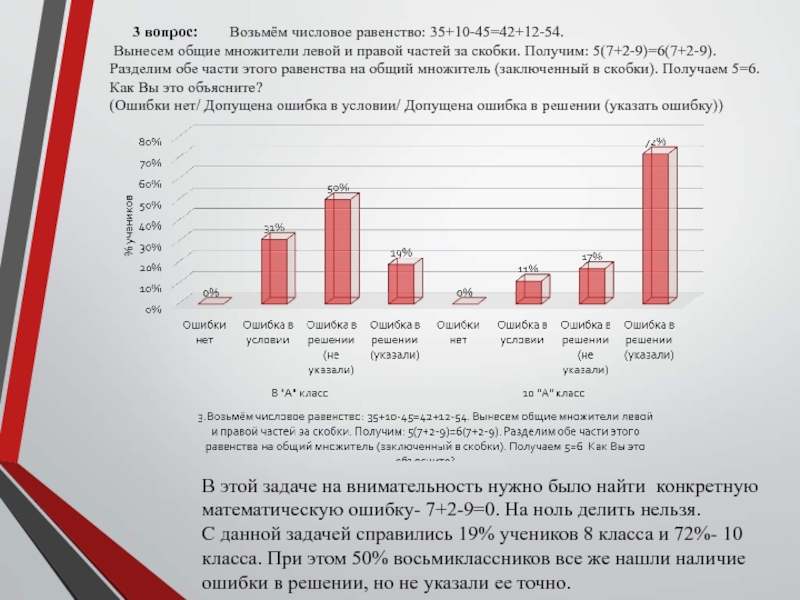
Слайд 20 3 вопрос: Возьмём числовое равенство: 35+10-45=42+12-54.
Вынесем
общие множители левой и правой частей за скобки. Получим: 5(7+2-9)=6(7+2-9).
Разделим обе части этого равенства на общий множитель (заключенный в скобки). Получаем 5=6.
Как Вы это объясните?
(Ошибки нет/ Допущена ошибка в условии/ Допущена ошибка в решении (указать ошибку))
В этой задаче на внимательность нужно было найти конкретную
математическую ошибку- 7+2-9=0. На ноль делить нельзя.
С данной задачей справились 19% учеников 8 класса и 72%- 10
класса. При этом 50% восьмиклассников все же нашли наличие
ошибки в решении, но не указали ее точно.
Слайд 214 вопрос: Дано уравнение x-a=0. Разделив обе части этого уравнения
на x-a, получим, что 1=0. Поскольку это равенство неверное, то
это означает, что исходное уравнение не имеет корней. Допущена ли здесь ошибка, и если да, то какая?
(Ошибки нет/ Допущена ошибка в условии/ Допущена ошибка в решении (указать ошибку))
Ответом данной задачи было: Поскольку x=a – корень уравнения,
то, разделив на выражение x-a обе его части, мы потеряли этот корень и поэтому получили неверное равенство 1=0.
Верно на этот вопрос ответили 22% 8-классников и 67% 10-классников,
при этом наличие ошибки отметили 100% учеников обоих классов, то
есть явление софизма определили все!
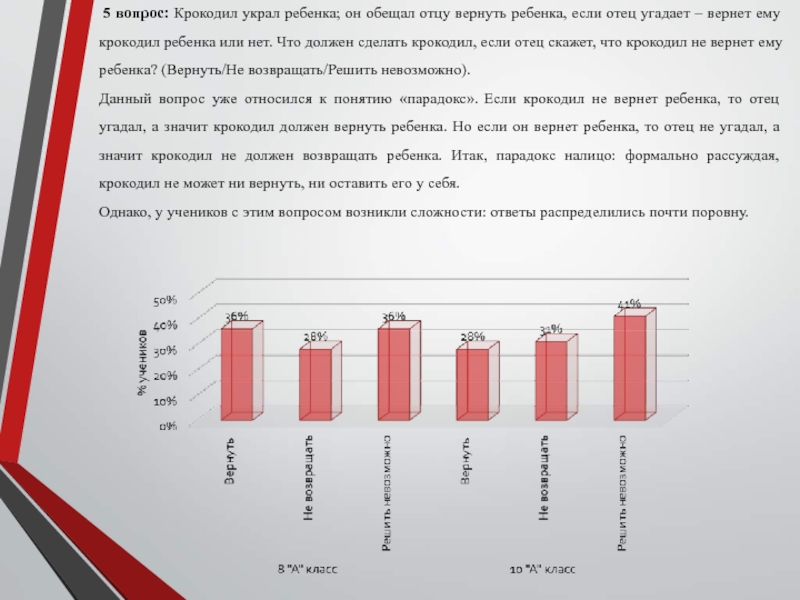
Слайд 22 5 вопрос: Крокодил украл ребенка; он обещал отцу вернуть
ребенка, если отец угадает – вернет ему крокодил ребенка или
нет. Что должен сделать крокодил, если отец скажет, что крокодил не вернет ему ребенка? (Вернуть/Не возвращать/Решить невозможно).Данный вопрос уже относился к понятию «парадокс». Если крокодил не вернет ребенка, то отец угадал, а значит крокодил должен вернуть ребенка. Но если он вернет ребенка, то отец не угадал, а значит крокодил не должен возвращать ребенка. Итак, парадокс налицо: формально рассуждая, крокодил не может ни вернуть, ни оставить его у себя.
Однако, у учеников с этим вопросом возникли сложности: ответы распределились почти поровну.
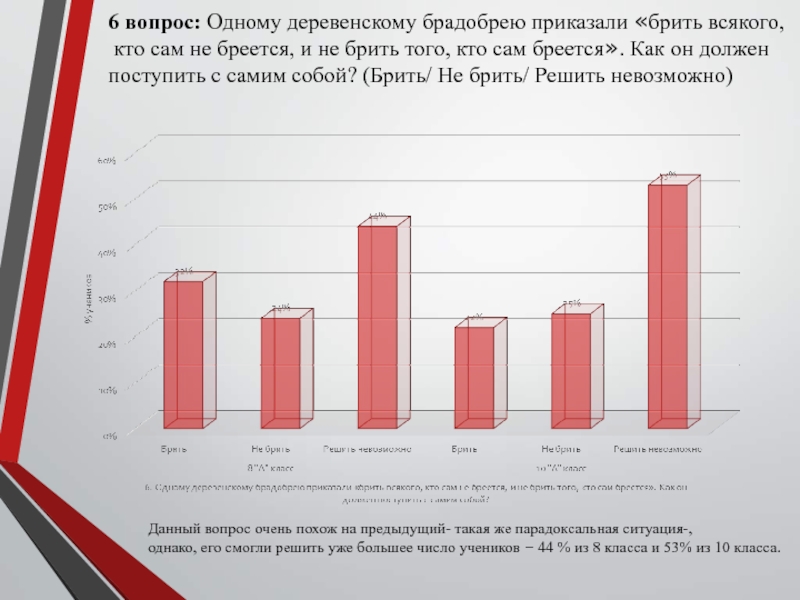
Слайд 236 вопрос: Одному деревенскому брадобрею приказали «брить всякого,
кто сам
не бреется, и не брить того, кто сам бреется». Как
он долженпоступить с самим собой? (Брить/ Не брить/ Решить невозможно)
Данный вопрос очень похож на предыдущий- такая же парадоксальная ситуация-,
однако, его смогли решить уже большее число учеников – 44 % из 8 класса и 53% из 10 класса.
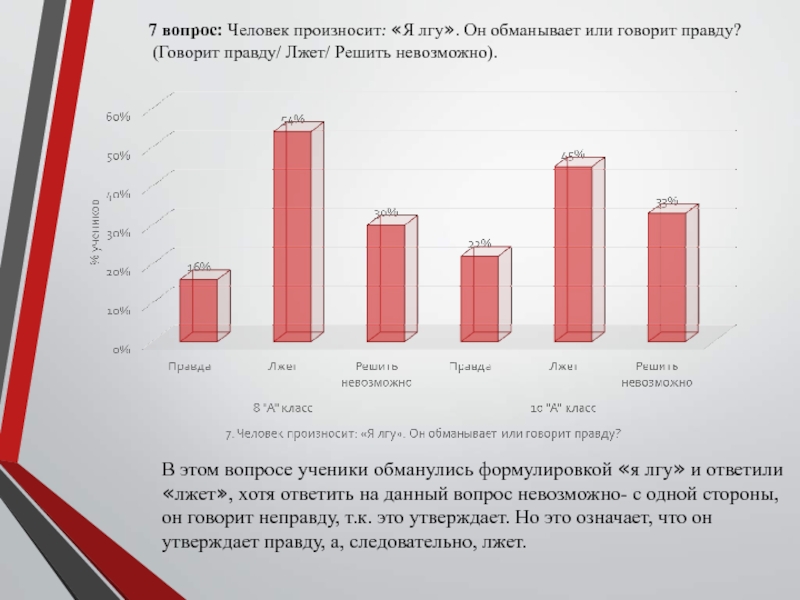
Слайд 247 вопрос: Человек произносит: «Я лгу». Он обманывает или говорит
правду?
(Говорит правду/ Лжет/ Решить невозможно).
В этом вопросе ученики обманулись
формулировкой «я лгу» и ответили «лжет», хотя ответить на данный вопрос невозможно- с одной стороны,
он говорит неправду, т.к. это утверждает. Но это означает, что он утверждает правду, а, следовательно, лжет.
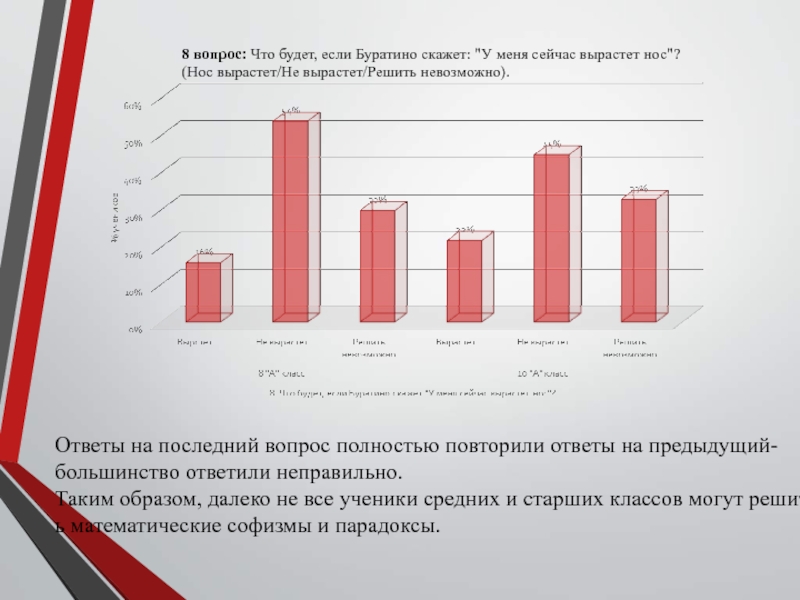
Слайд 258 вопрос: Что будет, если Буратино скажет: "У меня сейчас
вырастет нос"?
(Нос вырастет/Не вырастет/Решить невозможно).
Ответы на последний вопрос полностью
повторили ответы на предыдущий- большинство ответили неправильно.
Таким образом, далеко не все ученики средних и старших классов могут решит
ь математические софизмы и парадоксы.
Слайд 26Заключение
О математических софизмах и парадоксах можно говорить бесконечно много, как
и о математике в целом. Изо дня в день рождаются
новые софизмы и парадоксы, некоторые из них останутся в истории, а некоторые просуществуют один день.Софистика-это целая наука, а математические софизмы – это лишь часть одного большого течения. Поиск заключенных в софизме ошибок, ясное понимание их причин ведет к осмысленному изучению математики. Обнаружение и анализ ошибки, заключенной в софизме, очень часто оказывается более поучительным, чем просто разбор решений «безошибочных» задач. Эффектная демонстрация «доказательства» явно неверного результата, демонстрация того, к какой нелепице приводит пренебрежение каким-либо математическим правилом, и последующий поиск и разбор ошибки, позволяют понять и «закрепить» математическое правило или утверждение.
Что касается меня, то некоторые софизмы приходилось разбирать по нескольку раз, чтобы действительно в них разобраться, некоторые же наоборот, казались очень простыми. Исторические сведения о софистике и софистах помогли мне разобраться, откуда же все-таки началась история софизмов.
Парадоксы – это неожиданные утверждения, противоречащие здравому смыслу или общепризнанным научным теориям. Очень часто их рассматривают как ошибки, хотя в большинстве случаев они таковыми не являются. Обычно парадоксы построены на логически верных заключениях, но их противоречивый результат не является преднамеренным (этим они отличаются от софизмов). Парадоксы известны науке уже более двух тысяч лет. В античные времена были описаны многие парадоксы и для некоторых из них ученые до сих пор не могут найти объяснения и решения. Открываются парадоксы и в наши дни. Обычно подобные открытия сопровождаются кризисами в науке, разрушением старых, проверенных временем теорий и попытками создать новые, которые способны объяснить появившиеся противоречия. Количество существующих парадоксов по-настоящему огромное. Они присутствуют везде – и в повседневной жизни, и в науке. Практически в каждой научной области исследования существуют свои парадоксы.
Прослеживая историю математики, можно сказать, что во все времена математику спасала какая-нибудь новая идея. Она придавала математике строгость, восстанавливая ее авторитет. Поэтому не стоит бояться парадоксов, ибо они являются двигателями науки.
Благодаря софизмам и парадоксам можно научиться искать ошибки в рассуждениях других, научится грамотно строить свои рассуждения и логические объяснения.