Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Конспект урока-зачета по алгебре 8 класс "Квадратные уравнения"
Содержание
- 1. Конспект урока-зачета по алгебре 8 класс "Квадратные уравнения"
- 2. КВАДРАТНЫЕ УРАВНЕНИЯ урок-зачет Автор
- 3. ЦЕЛЬ: Обобщить и систематизировать знания учащихся по
- 4. ЗАПИШИТЕ ПРОПУЩЕННЫЕ СЛОВАI ТУР Каждый правильный ответоценивается в один балл
- 5. КВАДРАТНЫМ НАЗЫВАЕТСЯ УРАВНЕНИЕ ВИДА . . .
- 6. 5. ЕСЛИ D > 0,
- 7. 9 – 10. ЕСЛИ Х1 И
- 8. II ТУРВЫПОЛНИ УКАЗАННЫЕ ДЕЙСТВИЯ
- 9. ЗАПИШИТЕ КВАДРАТНОЕ УРАВНЕНИЕ, У КОТОРОГО ПЕРВЫЙ КОЭФФИЦИЕНТ
- 10. ЗАПИШИТЕ, ЧЕМУ РАВНА СУММА И ПРОИЗВЕДЕНИЕ КОРНЕЙ
- 11. III турНайдите соответствие между (1 – 4) и (А – Д)
- 12. 1. КАКОЕ ИЗ ДАННЫХ УРАВНЕНИЙ
- 13. 2. РЕШИТЕ УРАВНЕНИЕ ( 1 - 4).
- 14. 3. ДЛЯ КАЖДОГО ИЗ УРАВНЕНИЙ ( 1
- 15. ЗАЧЕТ ОКОНЧЕН СПАСИБО
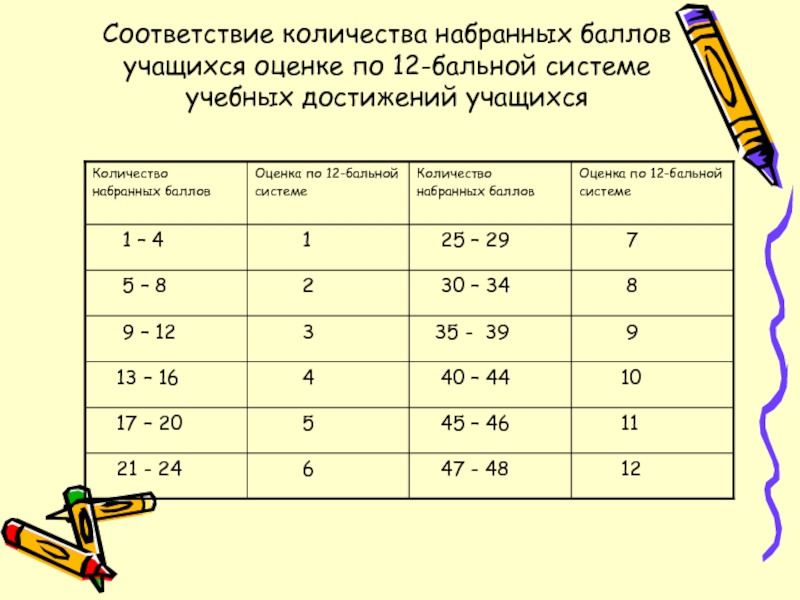
- 16. Соответствие количества набранных баллов учащихся оценке по 12-бальной системе учебных достижений учащихся
- 17. Отлично знать основы математики – это значит
- 18. Скачать презентанцию
КВАДРАТНЫЕ УРАВНЕНИЯ урок-зачет Автор презентации Белоусова Н.Н. учитель математики БСОШ № 4 г. Бахчисарай, Республика Крым
Слайды и текст этой презентации
Слайд 2
КВАДРАТНЫЕ
УРАВНЕНИЯ
урок-зачет
Автор презентации Белоусова Н.Н. учитель математики БСОШ № 4
г. Бахчисарай, Республика Крым
Слайд 3ЦЕЛЬ: Обобщить и систематизировать знания учащихся по теме «Квадратные уравнения»;
проверить умения применять их при решении задач; развивать математическую речь
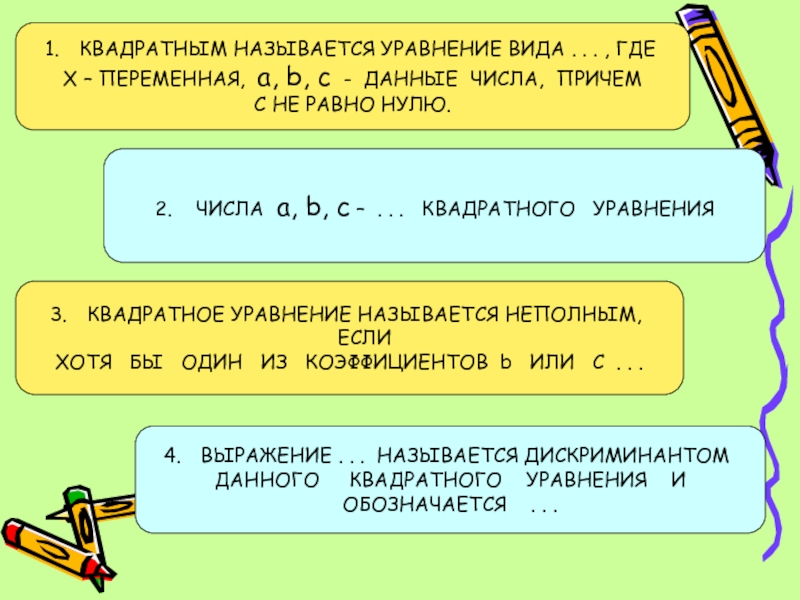
и логическое мышление; активизировать познавательную деятельность учащихся; прививать интерес к математике; учить умению рационально использовать время.
Слайд 5КВАДРАТНЫМ НАЗЫВАЕТСЯ УРАВНЕНИЕ ВИДА . . . , ГДЕ
Х –
ПЕРЕМЕННАЯ, a, b, c - ДАННЫЕ ЧИСЛА, ПРИЧЕМ
С НЕ
РАВНО НУЛЮ.2. ЧИСЛА a, b, c – . . . КВАДРАТНОГО УРАВНЕНИЯ
КВАДРАТНОЕ УРАВНЕНИЕ НАЗЫВАЕТСЯ НЕПОЛНЫМ, ЕСЛИ
ХОТЯ БЫ ОДИН ИЗ КОЭФФИЦИЕНТОВ b ИЛИ С . . .
ВЫРАЖЕНИЕ . . . НАЗЫВАЕТСЯ ДИСКРИМИНАНТОМ
ДАННОГО КВАДРАТНОГО УРАВНЕНИЯ И
ОБОЗНАЧАЕТСЯ . . .
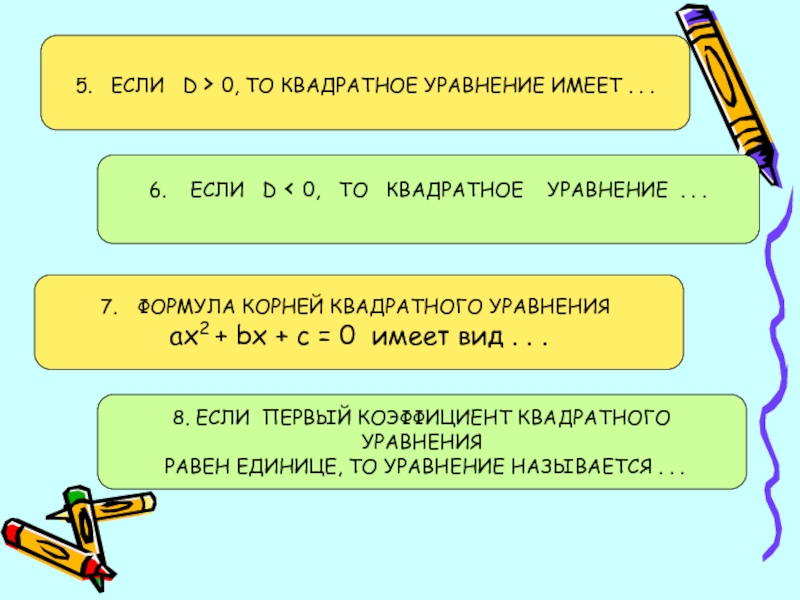
Слайд 65. ЕСЛИ D > 0, ТО КВАДРАТНОЕ УРАВНЕНИЕ
ИМЕЕТ . . .
6. ЕСЛИ D < 0,
ТО КВАДРАТНОЕ УРАВНЕНИЕ . . .8. ЕСЛИ ПЕРВЫЙ КОЭФФИЦИЕНТ КВАДРАТНОГО УРАВНЕНИЯ
РАВЕН ЕДИНИЦЕ, ТО УРАВНЕНИЕ НАЗЫВАЕТСЯ . . .
ФОРМУЛА КОРНЕЙ КВАДРАТНОГО УРАВНЕНИЯ
ax2 + bx + c = 0 имеет вид . . .
0, ТО КВАДРАТНОЕ УРАВНЕНИЕ ИМЕЕТ . ." alt="5. ЕСЛИ D > 0, ТО КВАДРАТНОЕ УРАВНЕНИЕ ИМЕЕТ . . .6. ЕСЛИ">Слайд 79 – 10. ЕСЛИ Х1 И Х2 КОРНИ ПРИВЕДЕННОГО
КВАДРАТНОГО
УРАВНЕНИЯ, ТО ИХ СУММА РАВНА
. . . УРАВНЕНИЯ, ВЗЯТОМУ С . . .
ЕСЛИ Х1 И Х2 КОРНИ ПРИВЕДЕННОГО КВАДРАТНОГО
УРАВНЕНИЯ, ТО ИХ ПРОИЗВЕДЕНИЕ РАВНО . . .
ЕСЛИ УРАВНЕНИЕ С ЦЕЛЫМИ КОЭФФИЦИЕНТАМИ, ИМЕЕТ
ЦЕЛЫЕ РЕШЕНИЯ, ТО ОНИ ЯВЛЯЮТСЯ ДЕЛИТЕЛЯМИ . . .
Слайд 9ЗАПИШИТЕ КВАДРАТНОЕ УРАВНЕНИЕ, У КОТОРОГО
ПЕРВЫЙ КОЭФФИЦИЕНТ РАВЕН 3, ВТОРОЙ
РАВЕН -5,
СВОБОДНЫЙ ЧЛЕН - 2
(1 б)ЗАПИШИТЕ ПРИВЕДЕННОЕ КВАДРАТНОЕ УРАВНЕНИЕ,
У КОТОРОГО ВТОРОЙ КОЭФФИЦИЕНТ И
СВОБОДНЫЙ ЧЛЕН - 2. (1б)
ЗАПИШИТЕ НЕПОЛНОЕ КВАДРАТНОЕ УРАВНЕНИЕ, У
КОТОРОГО ПЕРВЫЙ КОЭФФИЦИЕНТ РАВЕН – 5,
СВОБОДНЫЙ ЧЛЕН 20 И РЕШИТЕ ЕГО (2б)
ЗАПИШИТЕ НЕПОЛНОЕ КВАДРАТНОЕ УРАВНЕНИЕ, У
КОТОРОГО ПЕРВЫЙ КОЭФФИЦИЕНТ РАВЕН 3, ВТОРОЙ
КОЭФФИЦИЕНТ РАВЕН 5 И РЕШИТЕ ЕГО. (3б)
Слайд 10ЗАПИШИТЕ, ЧЕМУ РАВНА СУММА И ПРОИЗВЕДЕНИЕ
КОРНЕЙ ПРИВЕДЕННОГО
КВАДРАТНОГО
УРАВНЕНИЯ Х2 – 5Х + 6 = 0
(1б)ВЫЧИСЛИТЕ ДИСКРИМИНАНТ КВАДРАТНОГО УРАВНЕНИЯ
3Х2 – 8Х – 3 = 0. ( 1б)
НАЙДИТЕ КОРНИ КВАДРАТНОГО УРАВНЕНИЯ
2Х2 – 3Х – 2 = 0 (3б)
Слайд 121. КАКОЕ ИЗ ДАННЫХ УРАВНЕНИЙ ( 4 б)
–
Х2 + 1 = 0
Х2
= 1/Х + 3 Х4 – 5Х2 + 4 = 0
3Х2 – 5 Х + 2 = 0
А. ПОЛНОЕ
КВАДРАТНОЕ ?
Б. НЕ ЯВЛЯЕТСЯ
КВАДРАТНЫМ?
В. НЕ ПОЛНОЕ
КВАДРАТНОЕ?
Г. ЛИНЕЙНОЕ ?
Д. БИКВАДРАТНОЕ?
Слайд 132. РЕШИТЕ УРАВНЕНИЕ ( 1 - 4). КАЖДОМУ УРАВНЕНИЮ
ПОСТАВЬТЕ В
СООТВЕТСТВИЕ ВСЕ ЕГО РЕШЕНИЯ ( А – Д)
( 10 б)
3Х2
= 0 Х2 – 2Х = 0
Х2 – 9 = 0
Х2 + Х – 6 = 0
А. 0 ; 2
Б. 0
В. 3
Г. -3 ; 3
Д. -3 ; 2
Слайд 143. ДЛЯ КАЖДОГО ИЗ УРАВНЕНИЙ ( 1 – 4) ПОСТАВЬТЕ
В
СООТВЕТСТВИЕ СУММУ И ПРОИЗВЕДЕНИЕ ЕГО
КОРНЕЙ ( А _
Д) ( 10 б)1. Х2 – 7Х + 10 = 0
2.Х2 + 10Х + 21 = 0
3. Х2 + Х – 6 = 0
4. Х2 – Х – 6 = 0
А. -10; 21
Б. -1; - 6
В. 1 ; - 6
Г. 7; 10
Д. -7 ; - 10
Слайд 16Соответствие количества набранных баллов учащихся оценке по 12-бальной системе учебных
достижений учащихся
Слайд 17Отлично знать основы математики – это значит . . .
научиться находить математические задачи в жизненной практике . . .
научиться самим находить решения сложных задач, иногда необычного содержания . . . приучиться говорить кратко и четко. Андропов И. К.
