Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Конус геометрия 11 класс
Содержание
- 1. Конус геометрия 11 класс
- 2. История изучения геометрического тела конус. С именем
- 3. История изучения геометрического тела конус.Аполлоний Пергский- древнегреческий
- 4. История изучения геометрического тела конус.Строгое доказательство теорем,
- 5. История изучения геометрического тела конус.Архимед древнегреческий ученый,
- 6. Понятие конуса.Конус- это тело, ограниченное конической поверхностью
- 7. Понятие конуса.Коническая поверхность называется боковой поверхностью конуса,
- 8. Понятие конуса.Конус получен вращением прямоугольного треугольника АВС вокруг катета АВ.
- 9. Понятие конуса.Осевое сечение конуса.Если секущая плоскостьпроходит через
- 10. Площадь поверхности конуса.За площадь боковой поверхности конуса
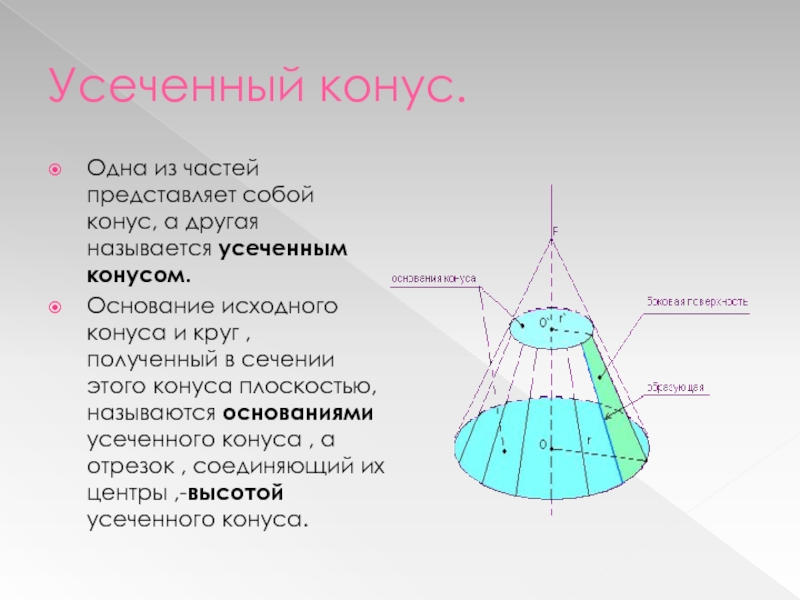
- 11. Усеченный конус.Одна из частей представляет собой конус,
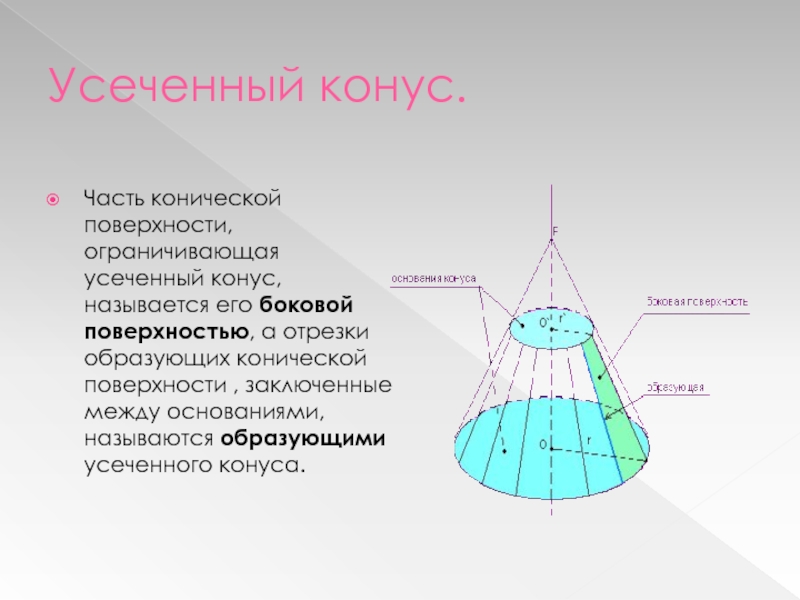
- 12. Усеченный конус.Часть конической поверхности, ограничивающая усеченный конус,
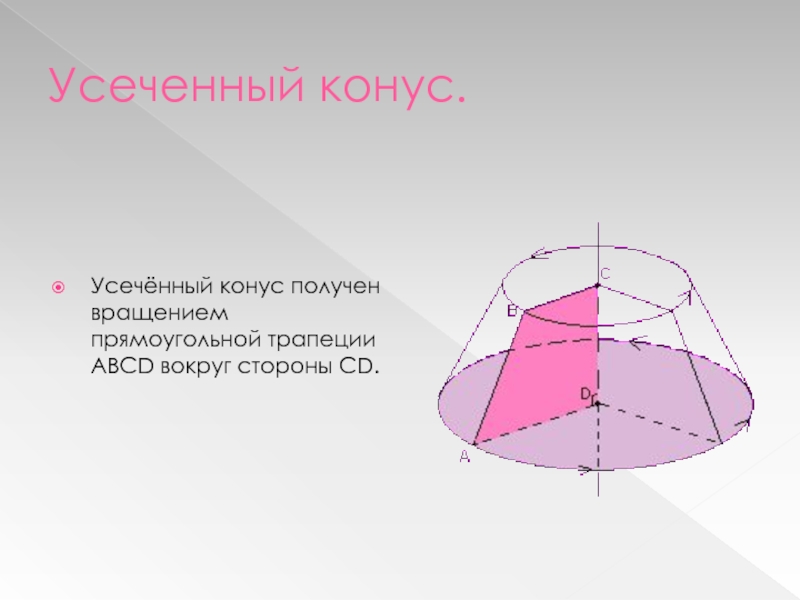
- 13. Усеченный конус.Усечённый конус получен вращением прямоугольной трапеции АВСD вокруг стороны CD.
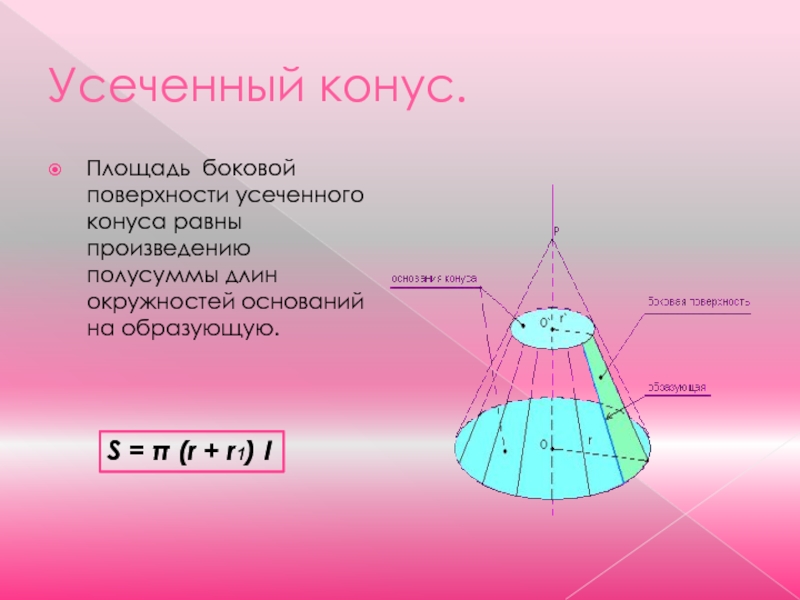
- 14. Усеченный конус.Площадь боковой поверхности усеченного конуса равны
- 15. Примеры конусов из жизни.Всех с наступающим Новым годом!
- 16. Спасибо за просмотр презентации!
- 17. Скачать презентанцию
История изучения геометрического тела конус. С именем Евклида связывают становление александрийской математики (геометрической алгебры) как науки. В XI книге «Начал» дается следующее определение: если вращающийся около одного из своих катетов прямоугольный
Слайды и текст этой презентации
Слайд 1История конуса
Понятие конуса
Площадь поверхности конуса
Усеченный конус
Примеры конусов из жизни
Конус.
Авторы презентации:
Сапоненко
Дмитрий и Трембач Наталья
Слайд 2История изучения геометрического тела конус.
С именем Евклида связывают становление александрийской
математики (геометрической алгебры) как науки.
В XI книге «Начал» дается следующее
определение: если вращающийся около одного из своих катетов прямоугольный треугольник слева вернется в то же самое положение, из которого он начал двигаться, то описанная фигура будет конусом.Евклид рассматривает только прямые конусы, т.е. такие, у которых ось перпендикулярна к основанию.
ЕВКЛИД
(330-275гг. до н.э.)
Слайд 3История изучения геометрического тела конус.
Аполлоний Пергский- древнегреческий математик и астроном,
ученик Евклида дал полное изложение теории и основанных им трудов
«Конические сечения» в восьми книгах.У Евклида нет понятия конической поверхности, оно было введено Аполлонием в его “Конических сечениях”, при этом он имел в виду обе плоскости конуса.
АПОЛЛОНИЙ ПЕРГСКИЙ
(260-170гг.до н. э.)
Слайд 4История изучения геометрического тела конус.
Строгое доказательство теорем, служащих для вывода
формулы объема конуса и изложенных в пяти предложениях 12 книги
“Начал” Евклида, дал Евдокс Книдский.ЕВДОКС КНИДСКИЙ
(408 - З55 гг.до.н.э )
Слайд 5История изучения геометрического тела конус.
Архимед древнегреческий ученый, математик и механик,
основоположник теоретической механики и гидростатики.
В «Началах» Евклида мы находим
определение только объёмов цилиндра и конуса, площадь же боковых поверхностей была найдена Архимедом. До нас дошло тринадцать трактатов Архимеда. В самом знаменитом из них — «О шаре и цилиндре» он доказал следующую теорему: «Поверхность всякого равнобедренного (т.е. прямого кругового) конуса, за вычетом основания, равна кругу, радиус которого есть средняя пропорциональная между стороной (т.е. образующей) конуса и радиуса круга, являющегося основанием конуса».
АРХИМЕД
(около 287 до н.э., Сиракузы,
Сицилия — 212 до н.э)
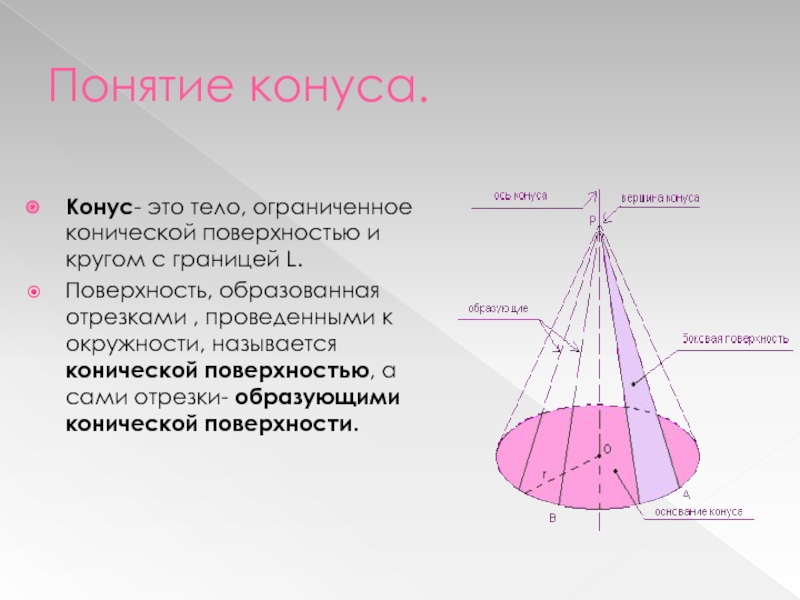
Слайд 6Понятие конуса.
Конус- это тело, ограниченное конической поверхностью и кругом с
границей L.
Поверхность, образованная отрезками , проведенными к окружности, называется конической
поверхностью, а сами отрезки- образующими конической поверхности.
Слайд 7Понятие конуса.
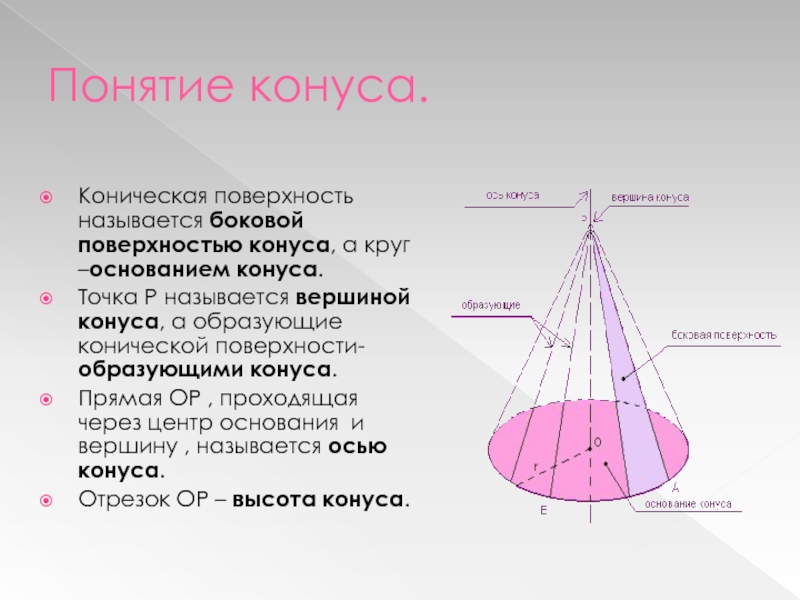
Коническая поверхность называется боковой поверхностью конуса, а круг –основанием
конуса.
Точка Р называется вершиной конуса, а образующие конической поверхности- образующими
конуса.Прямая ОР , проходящая через центр основания и вершину , называется осью конуса.
Отрезок ОР – высота конуса.
Слайд 9Понятие конуса.
Осевое сечение конуса.
Если секущая плоскость
проходит через ось конуса, то
сечение
представляет собой
равнобедренный треугольник,
основание которого- диаметр
основания конуса, а боковые
стороны- образующие
конуса. Это
сечение- осевое.
Слайд 10Площадь поверхности конуса.
За площадь боковой поверхности конуса принимается площадь ее
развертки.
Площадь боковой поверхности конуса равна произведению половины длины окружности основания
на образующую.Площадь полной поверхности конуса- сумма площадей боковой поверхности и основания.
Sбок. = П r l
Sкон.= П r (l+r)
Слайд 11Усеченный конус.
Одна из частей представляет собой конус, а другая называется
усеченным конусом.
Основание исходного конуса и круг , полученный в сечении
этого конуса плоскостью, называются основаниями усеченного конуса , а отрезок , соединяющий их центры ,-высотой усеченного конуса.
Слайд 12Усеченный конус.
Часть конической поверхности, ограничивающая усеченный конус, называется его боковой
поверхностью, а отрезки образующих конической поверхности , заключенные между основаниями,
называются образующими усеченного конуса.
Слайд 13Усеченный конус.
Усечённый конус получен вращением прямоугольной трапеции АВСD вокруг стороны
Слайд 14Усеченный конус.
Площадь боковой поверхности усеченного конуса равны произведению полусуммы длин
окружностей оснований на образующую.
S = π (r + r1) l
