Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Квадратичная функция,её свойства и график
Содержание
- 1. Квадратичная функция,её свойства и график
- 2. Психологическая установка учащимся:Продолжаем отрабатывать навыки исследования свойств
- 3. План урокаАктуализация знанийПрямоугольная система координат на плоскостиИспользование
- 4. залив Историишкола юнгпричал Повторительныйтаверна «Исследователь»о.Знатоковпирс Испытателейпляж «Надежда»Бурная гавань
- 5. 1.Что представляет собой траектория движения пиратов?2.Функцию какого
- 6. залив Историишкола юнгпричал Повторительныйтаверна «Исследователь»о.Знатоковпирс Испытателейпляж «Надежда»Бурная гавань
- 7. Более чем за 100 лет до нашей
- 8. Прямоугольная система координат на плоскостиОсь ординатОсь абсциссНачало координатКоординаты точки МАбсцисса точки МОрдината точки МОси координат
- 9. YXОпределите координаты зарытых кладов и получите сокровища
- 10. YXОпределите координаты зарытых кладов и получите сокровища
- 11. залив Историишкола юнгпричал Повторительныйтаверна «Исследователь»о.Знатоковпирс Испытателейпляж «Надежда»Бурная гавань
- 12. Определить:- координаты вершины параболы.-уравнение оси симметрии
- 13. Курс II1).Дана функция y= - 2x2 +
- 14. у = -182) у = -123)
- 15. Первые итоги урокаНа каком уровне ( на
- 16. Ваша оценка3Спасибо за работу.Попробуйте повысить оценку решением тестовых заданий
- 17. Ваша оценка4Спасибо за работу.Ваш уровень достаточно высок, но можете попробовать повысить его через решение тестовых заданий
- 18. Ваша оценка5Спасибо за работу.Ваша оценка очень высока. Попробуйте подтвердить ее решением тестовых заданий
- 19. залив Историишкола юнгпричал Повторительныйтаверна «Исследователь»о.Знатоковпирс Испытателейпляж «Надежда»Бурная гавань
- 20. Указания адмирала1.Получить тест-лист
- 21. залив Историишкола юнгпричал Повторительныйтаверна «Исследователь»о.Знатоковпирс Испытателейпляж «Надежда»Бурная гавань
- 22. В таверне рождаются умные мыслиДля каждого из
- 23. МОДУЛЬ
- 24. залив Историишкола юнгпричал Повторительныйтаверна «Исследователь»о.Знатоковпирс Испытателейпляж «Надежда»Бурная гавань
- 25. Используя алгоритм, постройте графики функций содержащих модуль
- 26. 3.Часть графика, для которой, значения функции отрицательны
- 27. Задания
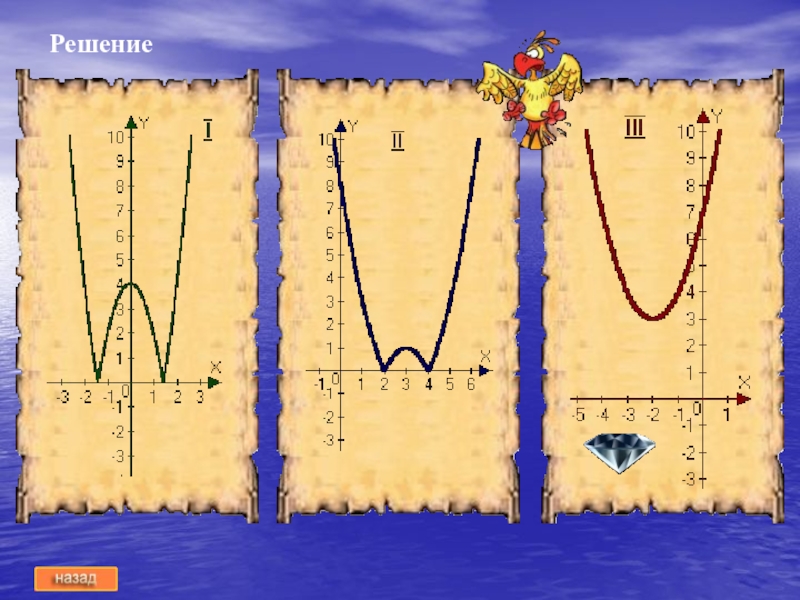
- 28. Решение
- 29. залив Историишкола юнгпричал Повторительныйтаверна «Исследователь»о.Знатоковпирс Испытателейпляж «Надежда»Бурная гавань
- 30. Квадратичные уравнения в баллистикеБаллистика - наука о
- 31. Квадратичные уравнения в космонавтикеВторая космическая скорость, наименьшая
- 32. Квадратичные уравнения в компьютерной графикеВ компьютерной графике
- 33. залив Историишкола юнгпричал Повторительныйтаверна «Исследователь»о.Знатоковпирс Испытателейпляж «Надежда»Бурная гавань
- 34. Правила написания синквейна: -первая строка – одно
- 35. Спасибо за внимание!
- 36. Скачать презентанцию
Слайды и текст этой презентации
Слайд 19 класс
готовимся
к экзаменам
Урок-путешествие
Квадратичная функция,
её свойства и график
Учитель математики: Айзатова
Фарида Фатхыловна
Слайд 2Психологическая установка учащимся:
Продолжаем отрабатывать навыки исследования свойств квадратичной функции и
построения их графиков. Формируем математическую интуицию, которая поможет ориентироваться в
построении графиков.На уроке можно ошибаться, сомневаться, консультироваться.
Дать самому себе установку: “Понять и быть тем первым, который увидит ход решения”
Цели урока:
Повторить свойства квадратичной функции
Закрепить их знание при построении графиков квадратичной функции
Уметь определять свойства функции по графику
Воспитывать умение контролировать внимание на всех этапах урока
Слайд 3План урока
Актуализация знаний
Прямоугольная система координат на плоскости
Использование свойств квадратичных функций
Математический
диктант
Первые итоги – самооценка
Самостоятельная работа - тестовое задание
Практическое задание-исследование функций
Построение
графиков функций, содержащих модульПрактическое использование квадратичных функций
Создание синквейна
“Алгебра щедра. Зачастую она дает больше, чем у нее спрашивают.”
Ж.Даламбер
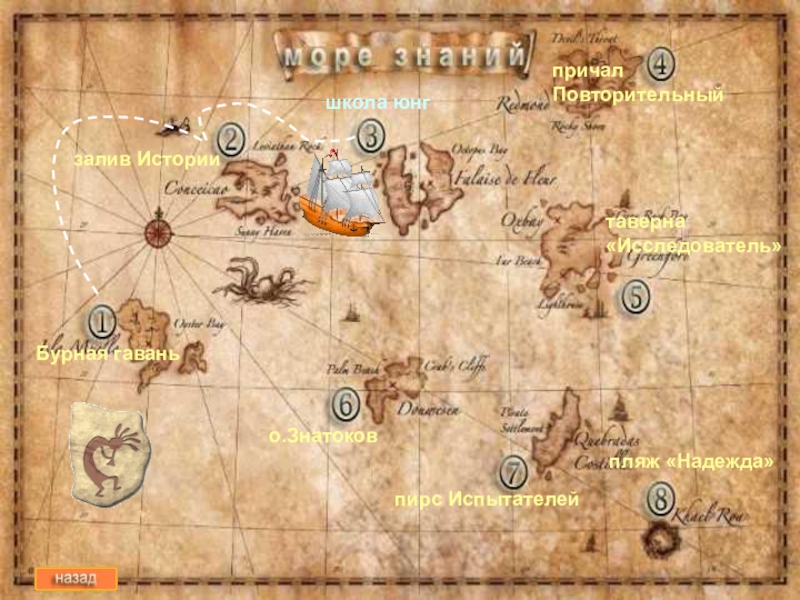
Слайд 4залив Истории
школа юнг
причал Повторительный
таверна «Исследователь»
о.Знатоков
пирс Испытателей
пляж «Надежда»
Бурная гавань
Слайд 51.Что представляет собой траектория движения пиратов?
2.Функцию какого вида называют квадратичной?
3.Где
расположен кристалл?
4.Как определить координаты вершины параболы?
5.Какой линией для параболы является
луч кристалла?6.Как расположены пираты относительно этой линии?
Слайд 6залив Истории
школа юнг
причал Повторительный
таверна «Исследователь»
о.Знатоков
пирс Испытателей
пляж «Надежда»
Бурная гавань
Слайд 7Более чем за 100 лет до нашей эры греческий ученый
Гиппарх предложил провести на карте Земли параллели и меридианы.
В
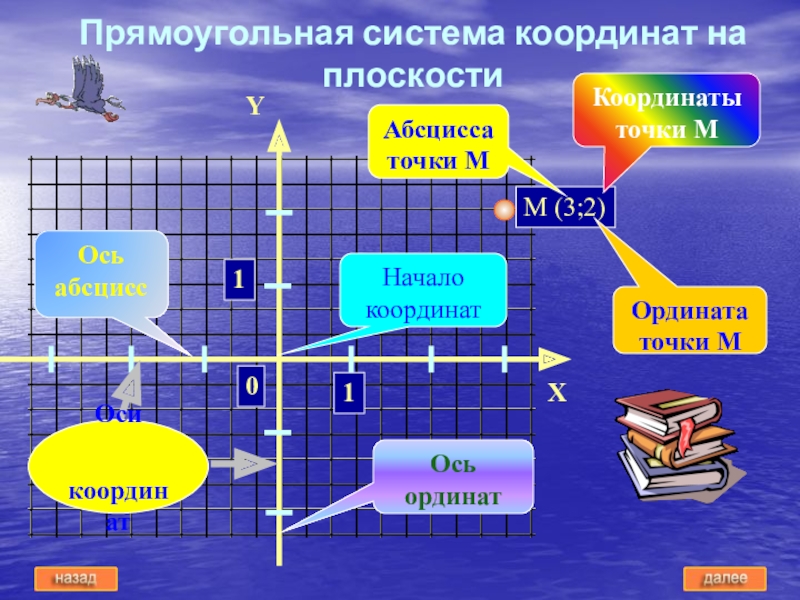
ХIV веке французский ученый Оресле по аналогии с географическими координатами создал координатную плоскость. Он поместил на плоскость прямоугольную сетку и назвал широтой и долготой то , что сейчас мы называем абсциссой и ординатой. Термины абсцисса и ордината были введены в употребление Лейбницем в XVII веке. Однако основная роль в создании метода координат принадлежит французскому ученому Рене Декарту (1596 –1650). Введенные на плоскости координаты х, у называют декартовыми.Слайд 8Прямоугольная система координат на плоскости
Ось ординат
Ось абсцисс
Начало координат
Координаты точки М
Абсцисса
точки М
Ордината точки М
Оси
координат
Слайд 9Y
X
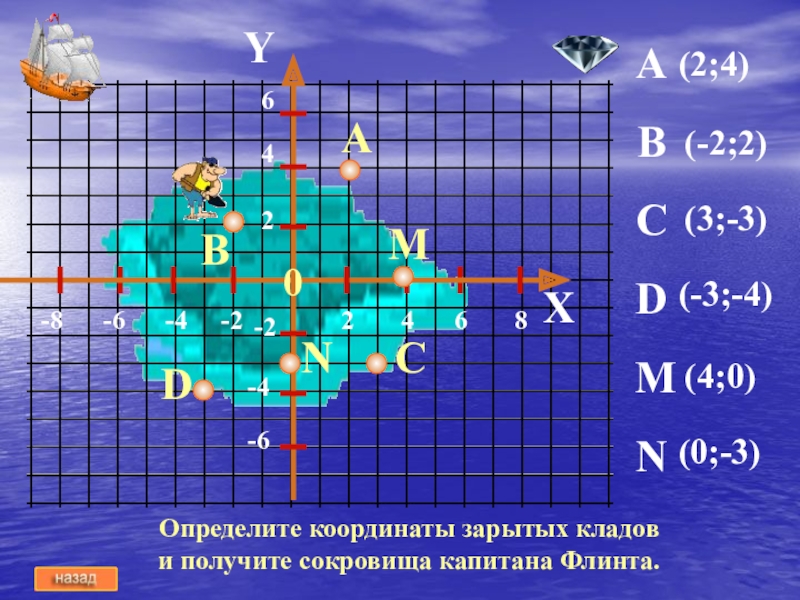
Определите координаты зарытых кладов и получите сокровища капитана Флинта.
А
0
-8
-6 -4 -2
2 4 6 8
В
С
D
N
M
-2
6
4
-4
-6
2
Слайд 10Y
X
Определите координаты зарытых кладов и получите сокровища капитана Флинта.
А
0
-8
-6 -4 -2
2 4 6 8
В
С
D
N
M
-2
6
4
-4
-6
2
A
B
C
D
M
N
(2;4)
(-2;2)
(3;-3)
(-3;-4)
(4;0)
(0;-3)
Слайд 11залив Истории
школа юнг
причал Повторительный
таверна «Исследователь»
о.Знатоков
пирс Испытателей
пляж «Надежда»
Бурная гавань
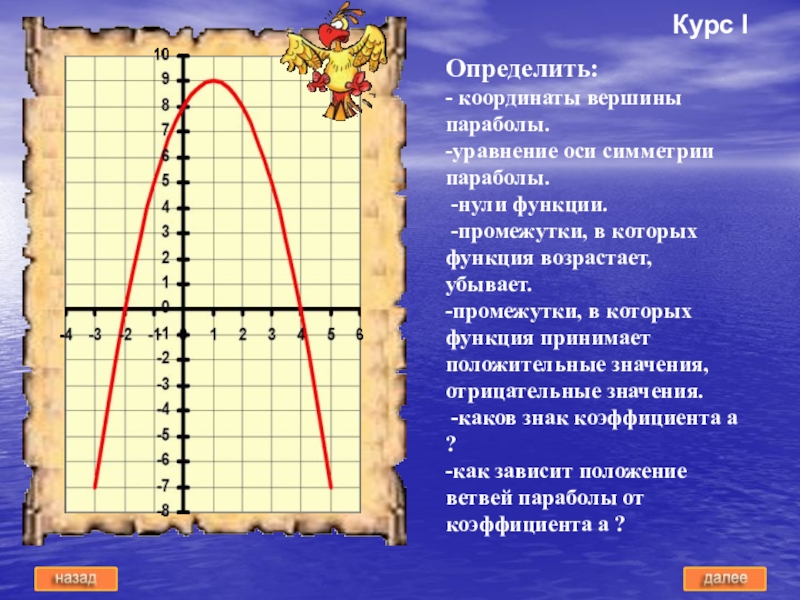
Слайд 12Определить:
- координаты вершины параболы.
-уравнение оси симметрии параболы.
-нули функции.
-промежутки, в которых функция возрастает, убывает.
-промежутки, в которых функция принимает
положительные значения, отрицательные значения.-каков знак коэффициента a ?
-как зависит положение ветвей параболы от коэффициента a ?
Курс I
Слайд 13Курс II
1).Дана функция y= - 2x2 + 3x - 4.
Найти значение y при x=-2.
2). Дана функция y=(x+2)(x-6). Найти
ординату точки пересечения графика этой функции с осью Оy.3). Определить абсциссу вершины параболы y=2x2 + 6x - 5.
4). Дана парабола y= 2(x-3)2 + 4. Найти сумму абсциссы и ординаты ее вершины.
5). Найти среднее арифметическое нулей функции
у = - х2 - 5х + 14.
Математический диктант
Слайд 15Первые итоги урока
На каком уровне ( на Ваш взгляд )
Вы
усвоили материал этого урока?
отличный
хороший
средний
(Щелкните левой кнопкой мышки на выбранном уровне)
Слайд 17Ваша оценка
4
Спасибо за работу.
Ваш уровень достаточно высок, но можете попробовать
повысить его через решение тестовых заданий
Слайд 18Ваша оценка
5
Спасибо за работу.
Ваша оценка очень высока. Попробуйте подтвердить ее
решением тестовых заданий
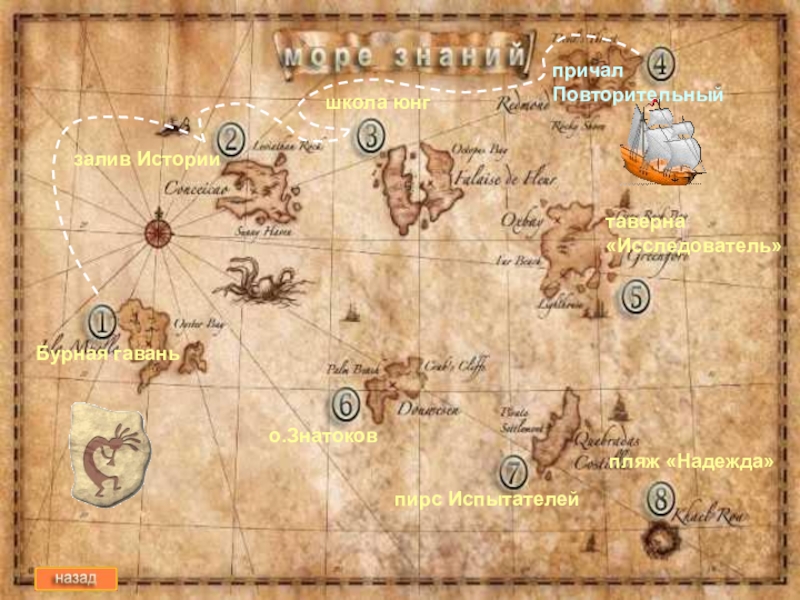
Слайд 19залив Истории
школа юнг
причал Повторительный
таверна «Исследователь»
о.Знатоков
пирс Испытателей
пляж «Надежда»
Бурная гавань
Слайд 20Указания адмирала
1.Получить тест-лист с
заданиями у консультанта
2.Выполнить предложенные задания в рабочей тетради
3.Заполнить таблицу результатов
в листе4.Сдать тест-лист консультанту
5.Сравнить полученный результат с самооценкой
6.Перейти к следующему разделу плана урока
Слайд 21залив Истории
школа юнг
причал Повторительный
таверна «Исследователь»
о.Знатоков
пирс Испытателей
пляж «Надежда»
Бурная гавань
Слайд 22В таверне рождаются умные мысли
Для каждого из уравнений, используя графики
квадратичных функций, подберите вершину параболы и прочитайте кодовое слово для
следующего этапа урокаГрафики смотри здесь
Слайд 24залив Истории
школа юнг
причал Повторительный
таверна «Исследователь»
о.Знатоков
пирс Испытателей
пляж «Надежда»
Бурная гавань
Слайд 263.Часть графика, для которой, значения функции отрицательны – зеркально отображаем
в верхнюю полуплоскость.
Алгоритм построения графика y = | x2
– 4 | 1.Строим график функции у = f(х).
2.Часть графика, для которой, значения функции положительны - оставляем без изменения.
Слайд 29залив Истории
школа юнг
причал Повторительный
таверна «Исследователь»
о.Знатоков
пирс Испытателей
пляж «Надежда»
Бурная гавань
Слайд 30Квадратичные уравнения в баллистике
Баллистика - наука о движении артиллерийских снарядов,
пуль, мин, авиабомб, реактивных снарядов, гарпунов и т.п. Снаряд будет
двигаться по траектории, которая описывается следующими уравнениями:Слайд 31Квадратичные уравнения в космонавтике
Вторая космическая скорость, наименьшая скорость (начальная), которую
нужно сообщить телу у поверхности Земли, чтобы оно, преодолев действие
земного притяжения, навсегда покинуло Землю. Вторая космическая скорость равна примерно 11,2 км/сек. Тело, обладающее второй космической скоростью, движется по отношению к Земле по параболической орбите; таким образом, вторая космическая скорость является параболической скоростью.Слайд 32Квадратичные уравнения в компьютерной графике
В компьютерной графике широко применяются уравнения
криволинейных функций.
Используя всего четыре квадратичные функции можно построить изображение этих
симпатичных очков.Слайд 33залив Истории
школа юнг
причал Повторительный
таверна «Исследователь»
о.Знатоков
пирс Испытателей
пляж «Надежда»
Бурная гавань
Слайд 34Правила написания синквейна:
-первая строка – одно слово (существительное);
-вторая
строка – два слова (прилагательные);
-третья строка – три слова
(глаголы );-четвертая строка – одно слово (существительное, отражающее Ваше отношение к тому, что написано в первой строке);
Напишите синквейн
по теме урока