Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Объём параллелепипеда. Единицы измерения объёма
Содержание
- 1. Объём параллелепипеда. Единицы измерения объёма
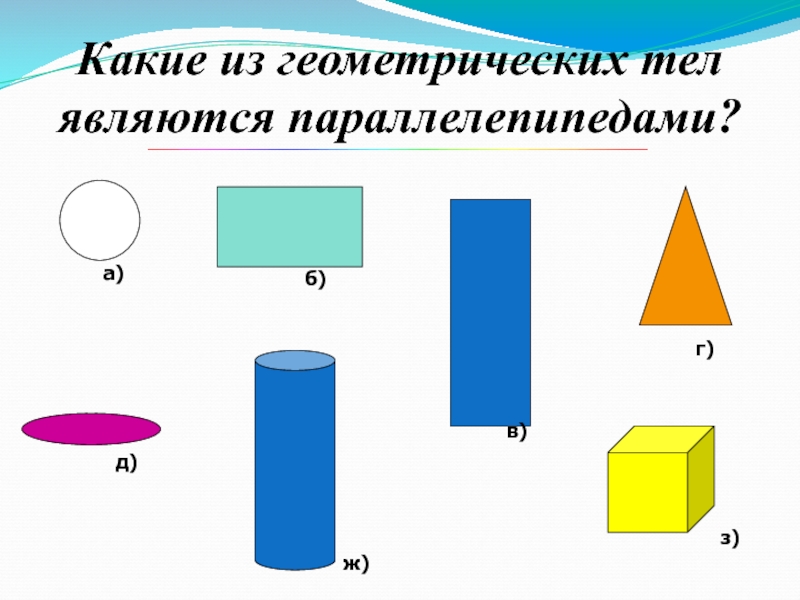
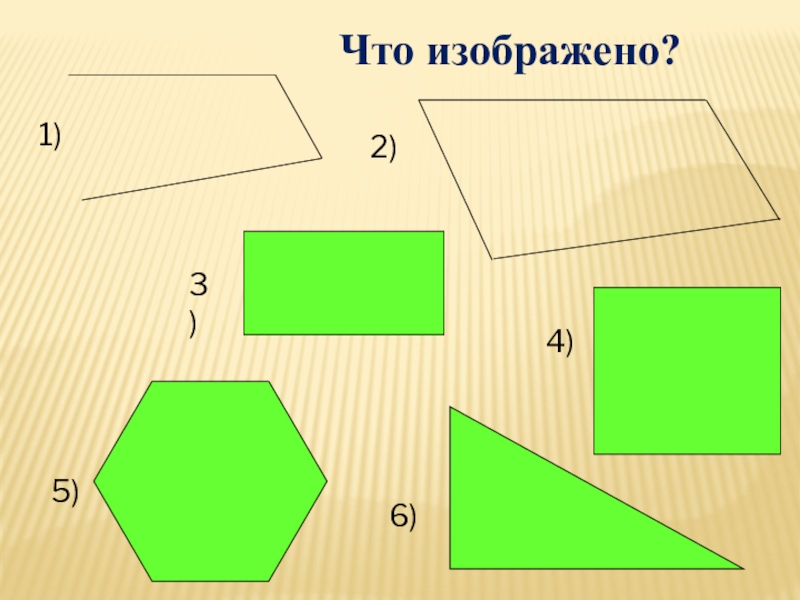
- 2. Какие из геометрических тел являются параллелепипедами?а)б)в)г)д)ж)з)
- 3. Прямоугольный параллелепипед
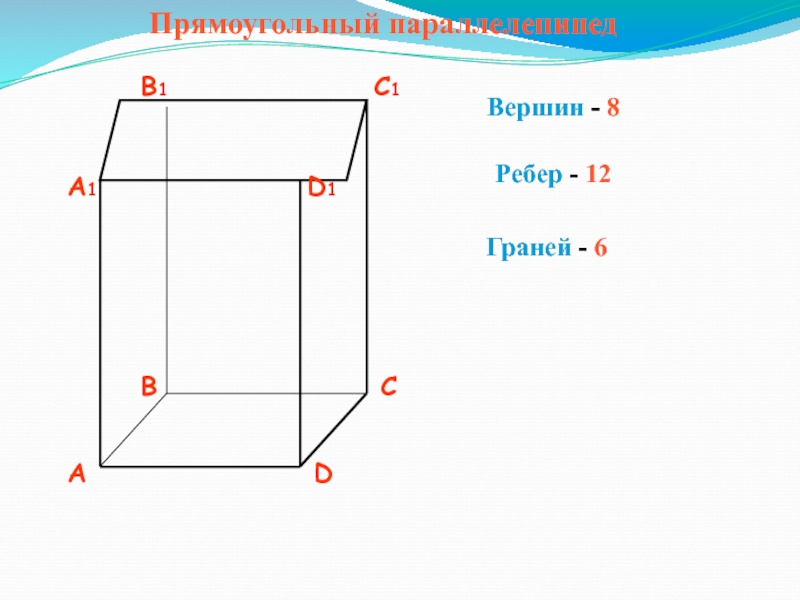
- 4. Прямоугольный параллелепипедВершин - 8Ребер - 12Граней - 6
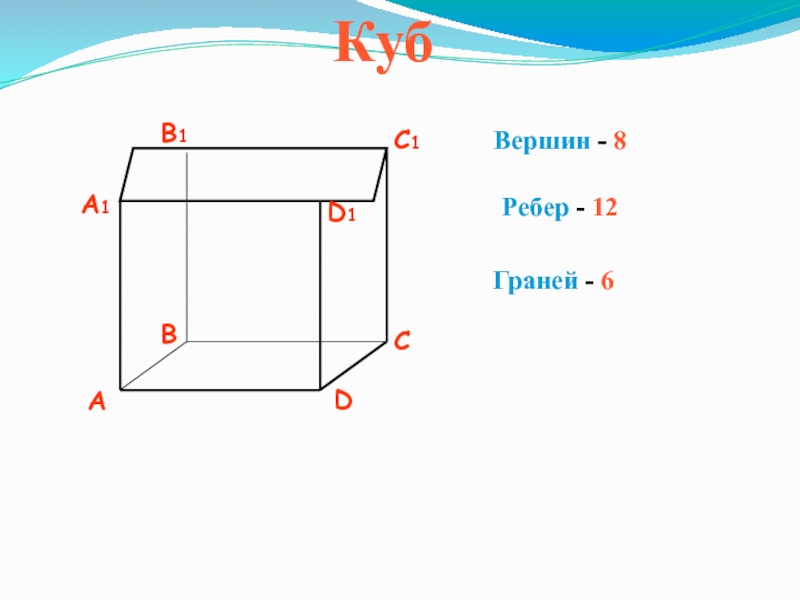
- 5. Куб
- 6. КубВершин - 8Ребер - 12Граней - 6
- 7. Что такое объем?
- 8. Слайд 8
- 9. Если наполнить формочку влажным песком, а потом
- 10. Величина части пространства, занимаемого геометрическим телом называется объемом этого тела.Что такое объемКак измерить эту величину?
- 11. Равные геометрические тела имеют одинаковые объёмы.Если геометрическое
- 12. Объёмы геометрических телобычно вычисляют,разбивая их на кубы,рёбрами
- 13. кубический сантиметр 1 см3кубический метр1 м3Кубический метр
- 14. Объём куба с ребром 1 дм —кубический
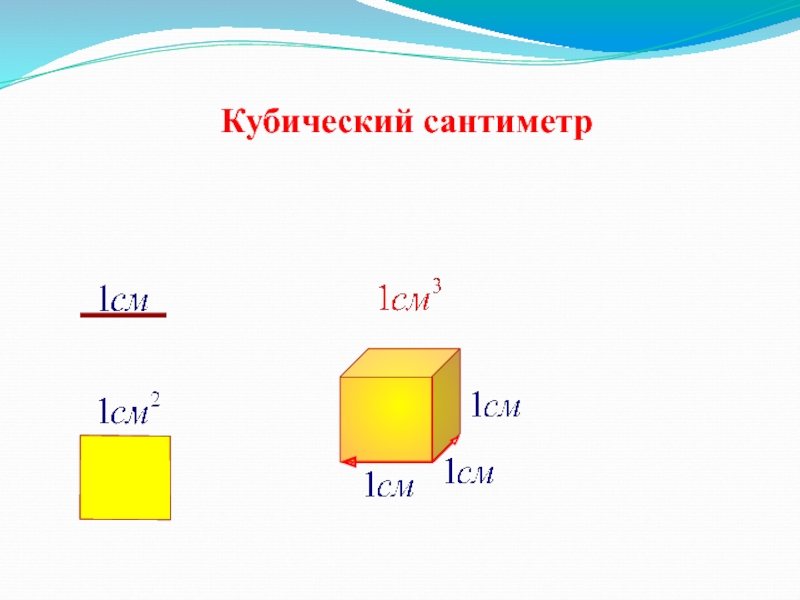
- 15. Кубический сантиметр
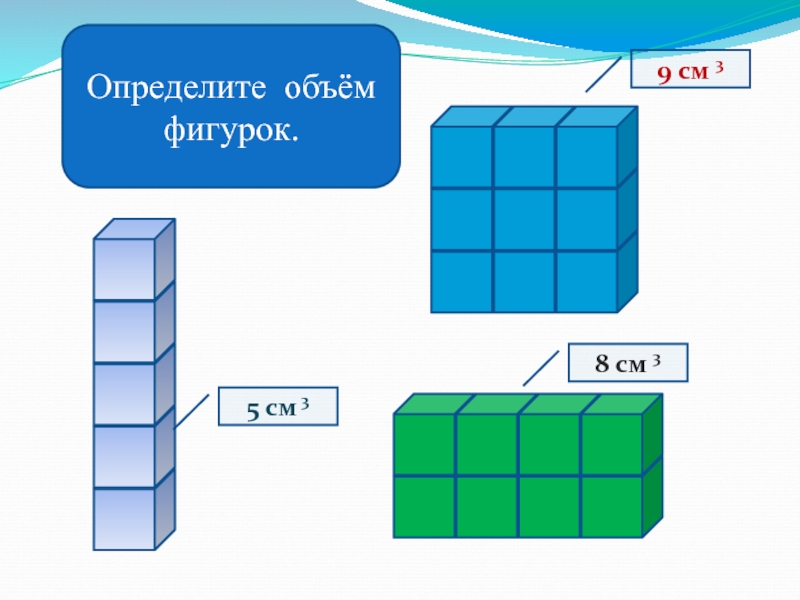
- 16. Определите объём фигурок.5 см 38 см 39 см 3
- 17. Будем вычислять объём в кубических сантиметрах.Уложим в
- 18. Чтобы заполнить этот параллелепипедединичными кубами полностью,надо выложить
- 19. ФормулаV - объемa, b, c – длины
- 20. 1.2.Два способа вычисления объёма параллелепипедаПлощадь основания умножить
- 21. Объём параллелепипеда равенпроизведению трёх его измерений:длины, ширины
- 22. Скачать презентанцию
Слайды и текст этой презентации
Слайд 10
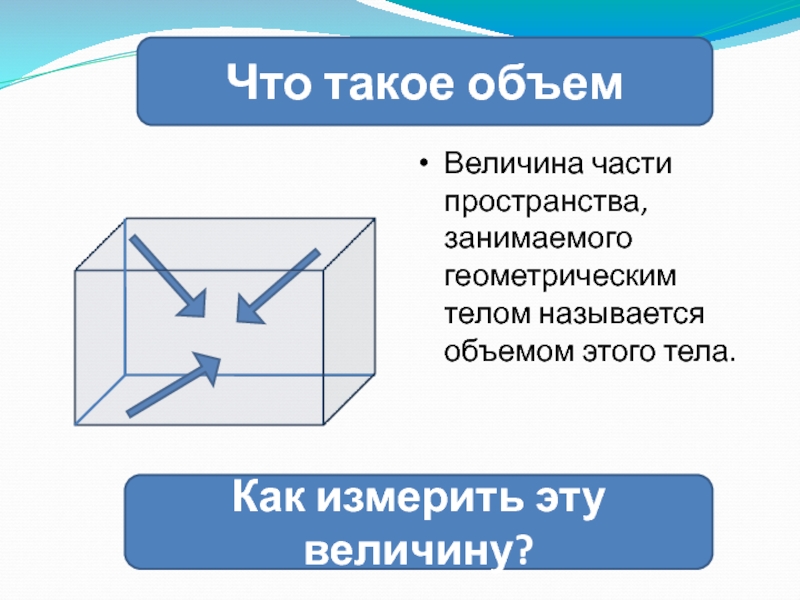
Величина части пространства, занимаемого геометрическим телом называется объемом этого тела.
Что
такое объем
Как измерить эту величину?
Слайд 11Равные геометрические тела имеют одинаковые объёмы.
Если геометрическое тело разбито на
несколько частей, то его
объём равен сумме объёмов этих частей.
Слайд 12Объёмы геометрических тел
обычно вычисляют,
разбивая их на кубы,
рёбрами которых являются
единичные отрезки.
Объём
куба с ребром 1 см
кубический сантиметр
1 см3
Объём куба с
ребром 1 мкубический метр
1 м3
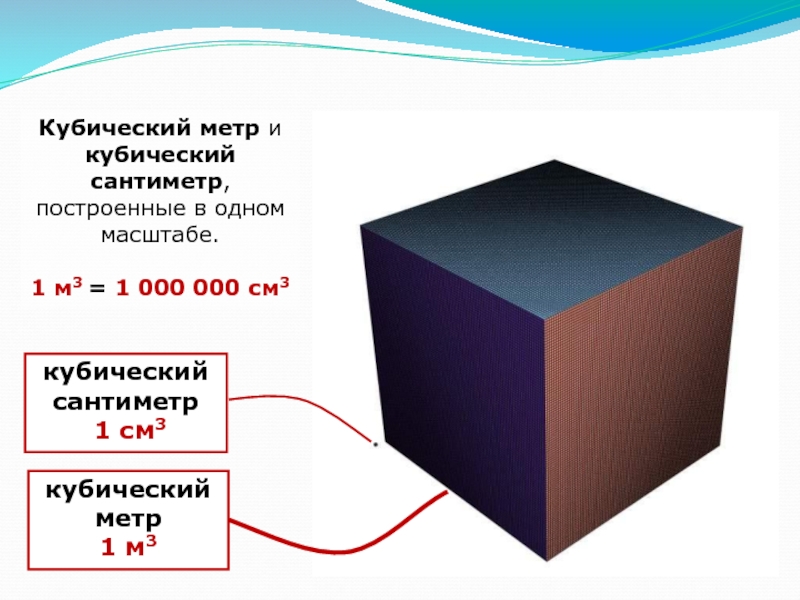
Слайд 13кубический сантиметр
1 см3
кубический метр
1 м3
Кубический метр и кубический сантиметр,
построенные в одном масштабе.
1 м3 = 1 000 000 см3
Слайд 14Объём куба с ребром 1 дм —
кубический дециметр (1 дм3).
Один
кубический дециметр
имеет и другое название — литр.
В литрах обычно измеряются
объёмы
сыпучих и жидких тел.кубический сантиметр
1 см3
кубический дециметр
1 дм3 (литр)
Литр
И
кубический сантиметр, построенные в одном масштабе.
1 л = 1 дм3
1 л = 1 000 см3
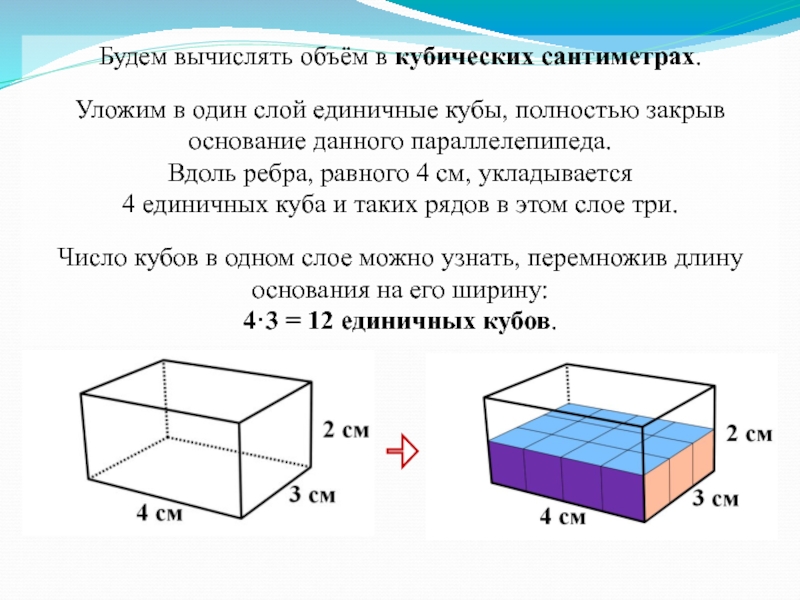
Слайд 17Будем вычислять объём в кубических сантиметрах.
Уложим в один слой единичные
кубы, полностью закрыв основание данного параллелепипеда.
Вдоль ребра, равного 4 см,
укладывается4 единичных куба и таких рядов в этом слое три.
Число кубов в одном слое можно узнать, перемножив длину основания на его ширину:
4·3 = 12 единичных кубов.
Слайд 18Чтобы заполнить этот параллелепипед
единичными кубами полностью,
надо выложить два таких слоя.
Для
этого понадобится
(4 · 3) ·2 = 24 единичных куба.
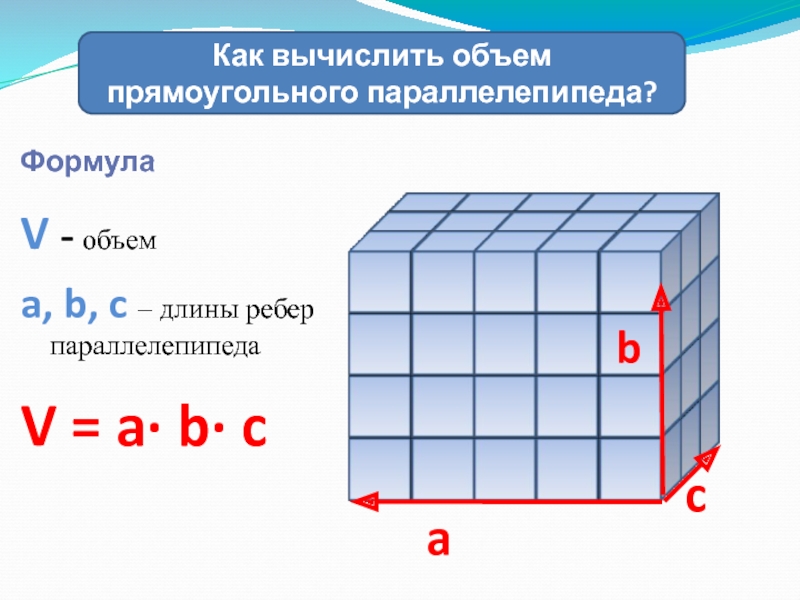
Слайд 19Формула
V - объем
a, b, c – длины ребер параллелепипеда
V =
a∙ b∙ c
Как вычислить объем прямоугольного параллелепипеда?
a
b
c
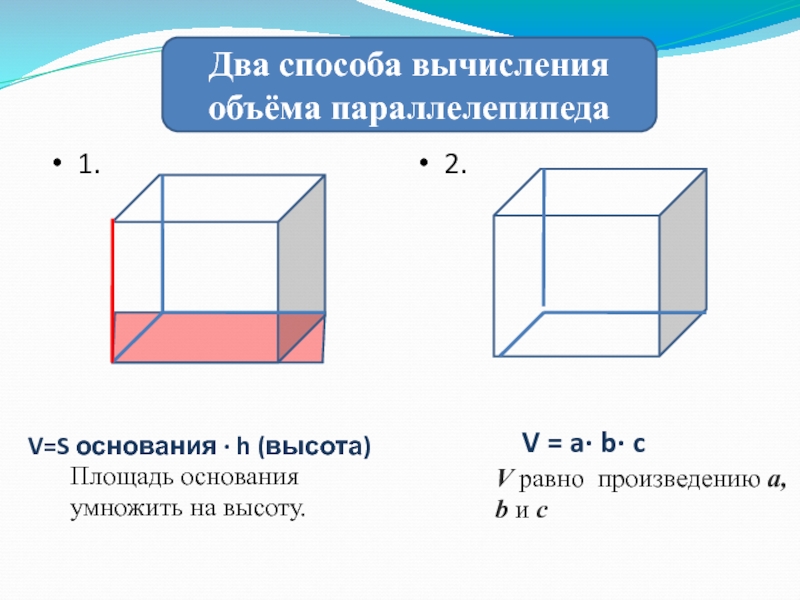
Слайд 20
1.
2.
Два способа вычисления объёма параллелепипеда
Площадь основания умножить на высоту.
V=S
основания ∙ h (высота)
V = a∙ b∙ c
V равно произведению
а, b и сСлайд 21Объём параллелепипеда равен
произведению трёх его измерений:
длины, ширины и высоты.
V =
a · b · c,
где V — объём;
а, b, c
– длина, ширина и высота параллелепипеда.Объём куба равен третьей
степени длины его ребра:
V = a3.