TheSlide.ru

Понятие цилиндра

Содержание

1. Понятие цилиндра
2. Цилиндры вокруг нас.
3. Цилиндрическая поверхность. Если в одной из
4. Точное название определенного выше тела – прямой
5. Цилиндры бывают прямыми и наклонными в зависимости
6. Высота, радиус и ось цилиндра. Радиусом
7. Вспомните формулу нахождения площади круга и найдите площадь основания цилиндра, радиус которого равен 2.4
8. Прямая, соединяющая центры оснований цилиндра, называется осью цилиндра.Сечение цилиндра, проходящее через ось, называется осевым сечением.
9. Найдите площадь осевого сечения цилиндра, если известны радиус его основания и высота.20
10. Цилиндр можно рассматривать как тело, полученное при вращении прямоугольника вокруг его стороны как оси.
11. Любое сечение боковой поверхности цилиндра плоскостью, перпендикулярной оси – это круг, равный основанию.
12. Пусть цилиндр пересекли плоскостью, перпендикулярной оси и получили круг площадью 3π. Чему равен радиус цилиндра?
13. Высота цилиндра 7 см, а радиус основания
14. Дано: цилиндр; Н = 7, R =
15. Проведем дополнительное построение: построим высоту трапеции, ее
16. Рассмотрим проекцию высоты трапеции на верхнее основание
17. Найдем высоту трапеции, ее площадь и искомый
18. Задача для самостоятельного решения. Расстояние от
19. Домашнее задание:П. 53, 54№№ 523, 525, 529.Спасибо за урок!
20. Скачать презентанцию

Цилиндры вокруг нас.

Слайды и текст этой презентации

Слайд 1Понятие цилиндра.
МОУ СОШ №256
г.Фокино

Понятие цилиндра.МОУ СОШ №256г.Фокино

Слайд 2Цилиндры вокруг нас.

Цилиндры вокруг нас.

Слайд 3Цилиндрическая поверхность.
Если в одной из двух параллельных плоскостей

взять окружность,
и из каждой ее точки восстановить

перпендикуляр до пересечения со второй плоскостью, то

получится тело, ограниченное двумя кругами и поверхностью, образованной из перпендикуляров.

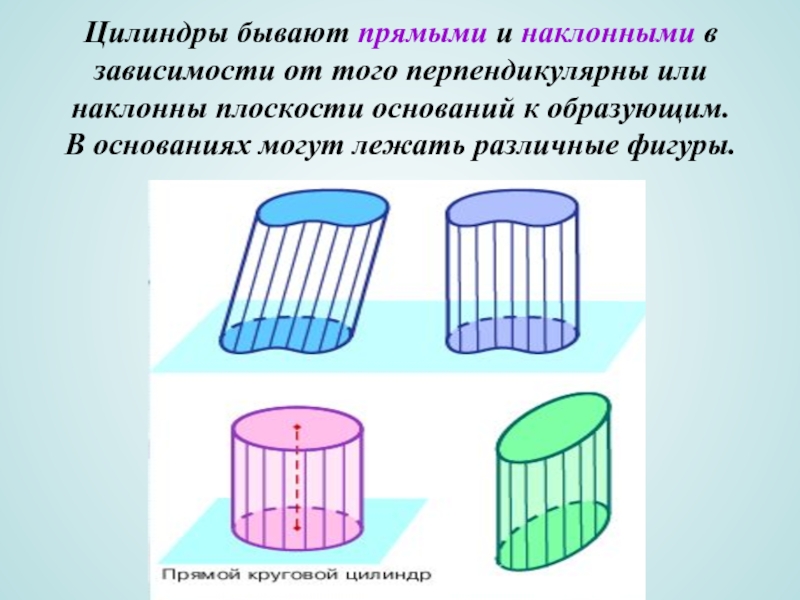
Это тело называется цилиндром.

Цилиндрическая поверхность. Если в одной из двух параллельных плоскостей взять окружность, и из каждой

Слайд 4Точное название определенного выше тела – прямой круговой цилиндр.

Вообще, цилиндр возникает при пересечении цилиндрической поверхности, образованной множеством параллельных

прямых, проведенных через каждую точку замкнутой кривой линии, и двух параллельных плоскостей.

Точное название определенного выше тела – прямой круговой цилиндр. Вообще, цилиндр возникает при пересечении цилиндрической поверхности,

Слайд 5Цилиндры бывают прямыми и наклонными в зависимости от того перпендикулярны

или наклонны плоскости оснований к образующим. В основаниях могут лежать

различные фигуры.

Цилиндры бывают прямыми и наклонными в зависимости от того перпендикулярны или наклонны плоскости оснований к образующим.

Слайд 6Высота, радиус и ось цилиндра.
Радиусом цилиндра наз. радиус

его основания.

Высотой цилиндра называется расстояние между плоскостями оснований.

Высота всегда равна образующей

Высота, радиус и ось цилиндра. Радиусом цилиндра наз. радиус его основания. Высотой цилиндра называется расстояние

Слайд 7Вспомните формулу нахождения площади круга и найдите площадь основания цилиндра,

радиус которого равен 2.
4

Вспомните формулу нахождения площади круга и найдите площадь основания цилиндра, радиус которого равен 2.4

Слайд 8Прямая, соединяющая центры оснований цилиндра, называется осью цилиндра.
Сечение цилиндра, проходящее

через ось, называется осевым сечением.

Прямая, соединяющая центры оснований цилиндра, называется осью цилиндра.Сечение цилиндра, проходящее через ось, называется осевым сечением.

Слайд 9Найдите площадь осевого сечения цилиндра, если известны радиус его основания

и высота.
20

Найдите площадь осевого сечения цилиндра, если известны радиус его основания и высота.20

Слайд 10Цилиндр можно рассматривать как тело, полученное при вращении прямоугольника вокруг

его стороны как оси.

Цилиндр можно рассматривать как тело, полученное при вращении прямоугольника вокруг его стороны как оси.

Слайд 11Любое сечение боковой поверхности цилиндра плоскостью, перпендикулярной оси – это

круг, равный основанию.

Любое сечение боковой поверхности цилиндра плоскостью, перпендикулярной оси – это круг, равный основанию.

Слайд 12Пусть цилиндр пересекли плоскостью, перпендикулярной оси и получили круг площадью

3π. Чему равен радиус цилиндра?

Пусть цилиндр пересекли плоскостью, перпендикулярной оси и получили круг площадью 3π. Чему равен радиус цилиндра?

Слайд 13Высота цилиндра 7 см, а радиус основания 5 см. В

цилиндре расположена трапеция так, что все ее вершины находятся на

окружностях оснований цилиндра. Найти площадь трапеции и угол между основанием и плоскостью трапеции, если параллельные стороны трапеции равны 6см и 8 см.

Задача.

Высота цилиндра 7 см, а радиус основания 5 см. В цилиндре расположена трапеция так, что все ее

Слайд 14Дано: цилиндр; Н = 7, R = 5

АВСD – трапеция,
АВ = 6, СD = 8
Найти: SABCD; угол между АВСD и основанием.

Дано: цилиндр; Н = 7, R = 5

Слайд 15Проведем дополнительное построение: построим высоту трапеции, ее проекцию на верхнее

основание цилиндра и перенесем параллельным переносом нижнее основание трапеции на

верхнее основание цилиндра.

НК – высота трапеции
НН1 – проекция НК на основание
Н1К = ОО1 = 7
С1D1 | | СD; С1D1 = CD

Проведем дополнительное построение: построим высоту трапеции, ее проекцию на верхнее основание цилиндра и перенесем параллельным переносом нижнее

Слайд 16Рассмотрим проекцию высоты трапеции на верхнее основание цилиндра.
ΔАОВ и ΔС1ОD1

–

равнобедренные.
АН = НВ → НВ = ½ АВ = 3.
С1Н1=Н1D1→Н1D1= ½С1D1=4

Из ΔОВН: ОН = 4.

Из ΔОD1Н1: ОН1 = 3.

НН1 = ОН + ОН1 =

7

Рассмотрим проекцию высоты трапеции на верхнее основание цилиндра.ΔАОВ и ΔС1ОD1 –

Слайд 17Найдем высоту трапеции, ее площадь и искомый угол.
НН1 =

7, Н1К = 7
ےН1НК = ےНКН1

= 450
НК = 7√2
SABCD = ½ (АВ + СD)*НК
SАВСD = 49√2

Найдем высоту трапеции, ее площадь и искомый угол. НН1 = 7, Н1К = 7

Слайд 18Задача для самостоятельного решения.
Расстояние от центра верхнего основания

до плоскости нижнего основания равно 6, а площадь осевого сечения

равна 72. Найдите расстояние от этого центра до хорды нижнего основания, стягивающей дугу в 900.

О1Н1 = 3√2

н1

Задача для самостоятельного решения. Расстояние от центра верхнего основания до плоскости нижнего основания равно 6, а

Слайд 19Домашнее задание:
П. 53, 54
№№ 523, 525, 529.

Спасибо за урок!

Домашнее задание:П. 53, 54№№ 523, 525, 529.Спасибо за урок!

Скачать презентацию

Теги

Обратная связь

Если не удалось найти и скачать доклад-презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:

Email: Нажмите что бы посмотреть

Что такое TheSlide.ru?

Это сайт презентации, докладов, проектов в PowerPoint. Здесь удобно хранить и делиться своими презентациями с другими пользователями.

Для правообладателей