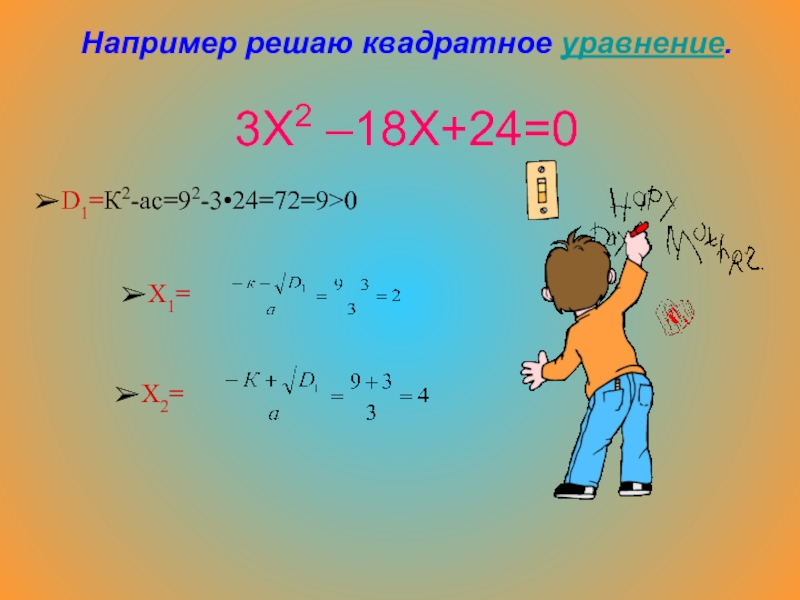Квадратные уравнения

ёщё в древности была вызвана потребностью решать задачи, связанные с

нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики. Квадратные уравнения умели решать около 2000 лет до нашей веры вавилоняне. Применяя современную алгебраическую запись, можно сказать, что в их  клинописных текстах  встречаются, кроме неполных, и такие, например, полные квадратные уравнения.
 

Квадратные уравнения в Древнем Вавилоне.

Немного из истории

с современным, однако неизвестно, каким образом дошли вавилоняне до этого

правила. Почти все найденные до сих пор клинописные тексты приводя только задачи с решениями, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены. Несмотря на высокий уровень развития алгебры в Вавилонии, в клинописных текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений.

их сумма равна -p, а произведение равно q, то есть x1

+ x2 = -p , x1 x2 = q
(сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену).

196 – 96 = 100
X1 = 2, X2

= 12
X1 + X2 = 14, X1•X2 = 24

Не верите? Проверьте!

значит корни имеют разные

знаки
Х1 + Х2 = – 3, значит больший по модулю
корень - отрицательный
Подбором находим корни: Х1 = – 5, Х2 = 2

Угадываем корни

x - переменная, a, b, c - некоторые числа, причем

a≠0.

.

Алгоритм решения квадратного уравнения:

если D>0, то данное квадратное уравнение имеет

два корня,которые равны