Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Квадратные уравнения через призму истории
Содержание
- 1. Квадратные уравнения через призму истории
- 2. Цель работы:проследить историю развития квадратных уравнений; отметить ученых, внесших свой вклад в развитие квадратных уравнений.
- 3. Кто хочет ограничиться настоящим без
- 4. Методы решения квадратных уравнений были
- 5. у25у5у25Как греки решали уравнение y2 + 10y
- 6. Диофант жил в четвертом веке нашей эры.
- 7. Учебник математики ал-Хорезми,
- 8. На сторонах квадрата
- 9. Квадратные уравнения в Европе XIII—XVII веков
- 10. Франсуа Виет — замечательный французский математик, положивший
- 11. Общее правило решения
- 12. Это сделал голландский математик Жирар Альберт в
- 13. Вывод формулы решения
- 14. Штифель (1486 – 1567, Германия) в 1544
- 15. Выводы: Развитие науки о решении квадратных
- 16. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Цель работы:
проследить историю развития квадратных уравнений;
отметить ученых, внесших свой вклад
в развитие квадратных уравнений.
Слайд 4 Методы решения квадратных уравнений были известны еще в
древние времена. Они излагались в вавилонских рукописях царя Хаммурапи(20в. до
н.э.), в трудах древнегреческого математика Евклида(3в. до н. э.), в древних китайских и японских трактатах. Многие математики древности решали квадратные уравнения геометрическим способом. Например, уравнение могло звучать так: квадрат и несколько его частей равны определенному числу.О чем свидетельствуют
клинописные тексты
Слайд 5у2
5у
5у
25
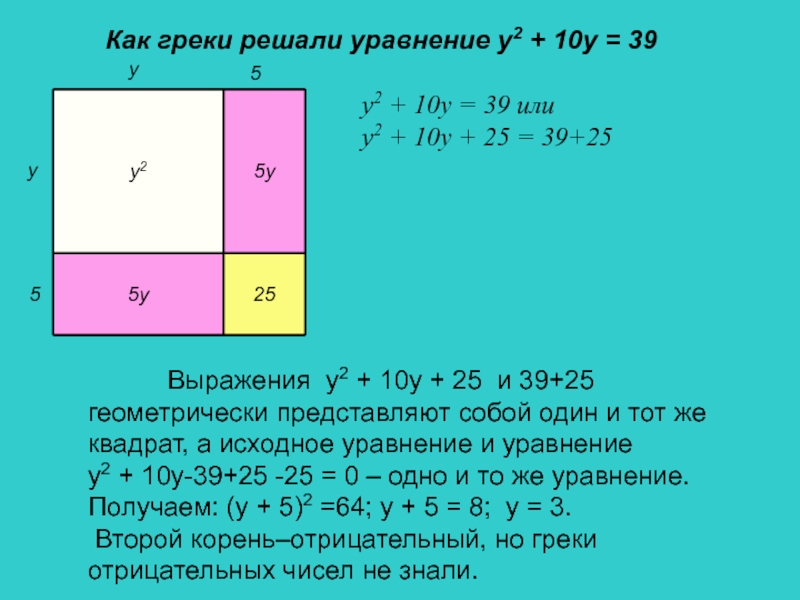
Как греки решали уравнение y2 + 10y = 39
5
у
у
5
Выражения у2 + 10y + 25
и 39+25 геометрически представляют собой один и тот же квадрат, а исходное уравнение и уравнениеy2 + 10y-39+25 -25 = 0 – одно и то же уравнение. Получаем: (у + 5)2 =64; у + 5 = 8; у = 3.
Второй корень–отрицательный, но греки отрицательных чисел не знали.
y2 + 10у = 39 или
у2 + 10y + 25 = 39+25
Слайд 6Диофант жил в четвертом веке нашей эры. Ученый отошел от
традиционных в греческой математике геометрических проблем и занялся алгеброй. Основное
его произведение „Арифметика". Сохранилось шесть томов из предполагаемых тринадцати; в них содержится 189 уравнений с решениями. Автор интересуется только одним решением: положительным и рациональным. Диофант не применял общих методов решения уравнений: методы у него меняются от одного уравнения к другому. При решении уравнений, чтобы получить желаемое рациональное и положительное число, Диофант применяет много остроумных приемов.Слайд 7 Учебник математики ал-Хорезми, выпущенный им около
830 года, посвящен в основном решению уравнений первой и второй
степени. Этот математик уравнения решает также геометрически. Рассмотрим, как решал ал – Хорезми тоже уравнение х2 +10х = 39. В оригинале эта задача формулируется следующим образом: «Квадрат и десять корней равны 39».Как решал квадратные уравнения
ал-Хорезми?
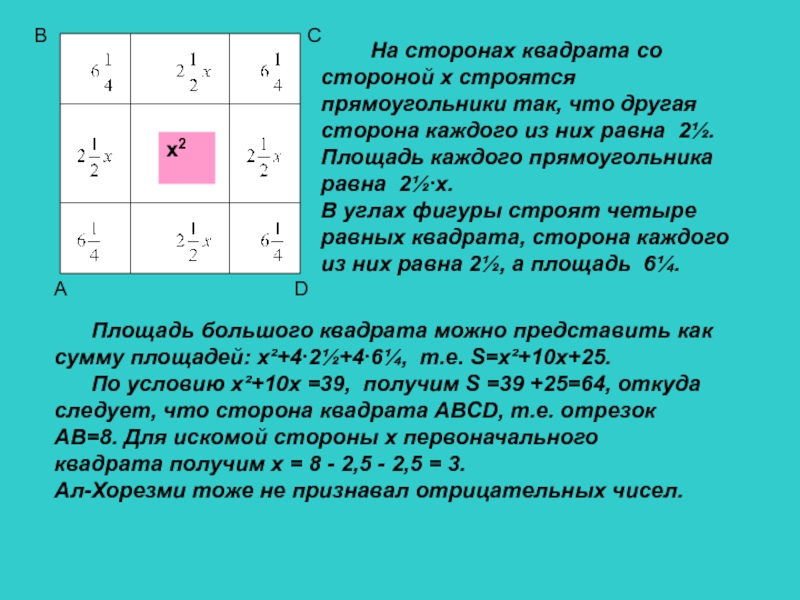
Слайд 8 На сторонах квадрата со стороной х
строятся прямоугольники так, что другая сторона каждого из них равна
2½. Площадь каждого прямоугольника равна 2½∙х.В углах фигуры строят четыре равных квадрата, сторона каждого из них равна 2½, а площадь 6¼.
Площадь большого квадрата можно представить как сумму площадей: х²+4∙2½+4∙6¼, т.е. S=x²+10x+25.
По условию х²+10х =39, получим S =39 +25=64, откуда следует, что сторона квадрата АВСD, т.е. отрезок АВ=8. Для искомой стороны х первоначального квадрата получим х = 8 - 2,5 - 2,5 = 3.
Ал-Хорезми тоже не признавал отрицательных чисел.
Слайд 9Квадратные уравнения в Европе XIII—XVII веков
Способы решения квадратных уравнений по образцу ал-Хорезми в Европе
были впервые изложены в «Книге абака», написанной в 1202 г. итальянским математиком Леонардо Фибоначчи. Его книга способствовала распространению алгебраических знаний не только в Италии, но и в Германии, Франции и других странах Европы. Многие задачи из «Книги абака» переходили почти во все европейские учебники XVI—XVII вв. и частично XVIII.Слайд 10 Франсуа Виет — замечательный французский математик, положивший начало алгебре как
науке о преобразовании выражений, о решении уравнений в общем виде;
создатель буквенного исчисления.Француа Виет
Слайд 11 Общее правило решения
квадратных уравнений,
приведенных
к виду
х2 + вх = с,
при всевозможных
комбинациях знаков коэффициентов b, с
было сформулировано в Европе
лишь в 1544 г.немецким
математиком
Михаэлем Штифелем.
Слайд 12Это сделал голландский математик Жирар Альберт в своем главном труде
«Новые открытия в алгебре» в 1629 году.
Жерар дал геометрическое объяснение
отрицательным корням уравнения как направленным отрезкам, первым признал нуль корнем уравнения, и, следовательно, числом.Кто вывел формулу корней
квадратного уравнения
Слайд 13 Вывод формулы решения квадратного уравнения в
общем виде имеется и у Виета, однако Виет признавал только
положительные корни. Итальянские математики Тарталья, Кардано, Бомбелли среди первых в XVI в. учитывают, помимо положительных, и отрицательные корни. Большой вклад внесли и другие математики.Слайд 14Штифель (1486 – 1567, Германия) в 1544 году сформировал общее
правило решения квадратных уравнений, приведённых к единому каноническому виду х2
+ b x = c при всевозможных комбинациях знаков и коэффициентов b и c.Франсуа Виет (1540 – 1603, Франция) вывел формулы решения квадратного уравнения в общем виде, однако он признавал только положительные числа.
Итальянские учёные Тарталья (1500-1557), Кардано (1501-1576), Бомбелли (1526-1572) среди первых в XVI веке учитывают, помимо положительных, и отрицательные корни.
В XVII веке благодаря трудам Жирара (1595-1632, Голландия), Декарта (1596-1650, Франция), Ньютона (1643-1727, Англия) и других учёных, способ решения квадратных уравнений принимает современный вид.
Эти ученые внесли достойный вклад в развитие теории решения квадратных уравнений