Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
"Квадратты? функция"
Содержание
- 1. "Квадратты? функция"
- 2. Сабақтың мақсаты:Білімділік: y=ах2 функциясының графигінің қасиеттерін пайдалана
- 3. Қайталау сұрақтары:1. Функцияның берілу тәсілдерін атаңыз.2. y=ax2
- 4. у =ах2 функциясының қасиеттері және графигі
- 5. у =ах2 функциясының қасиеттері және графигіа
- 6. у =ах2 + bх + с түріндегі
- 7. “ Парабола ” деген атауды атақты грек ғалымы Аполлони енгізген.
- 8. Слайд 8
- 9. y=ax2 функциясының графигі арқылы у=ax2 +n және y=a(x-m)2 функцияларының графиктерін салуды қарастырамыз.
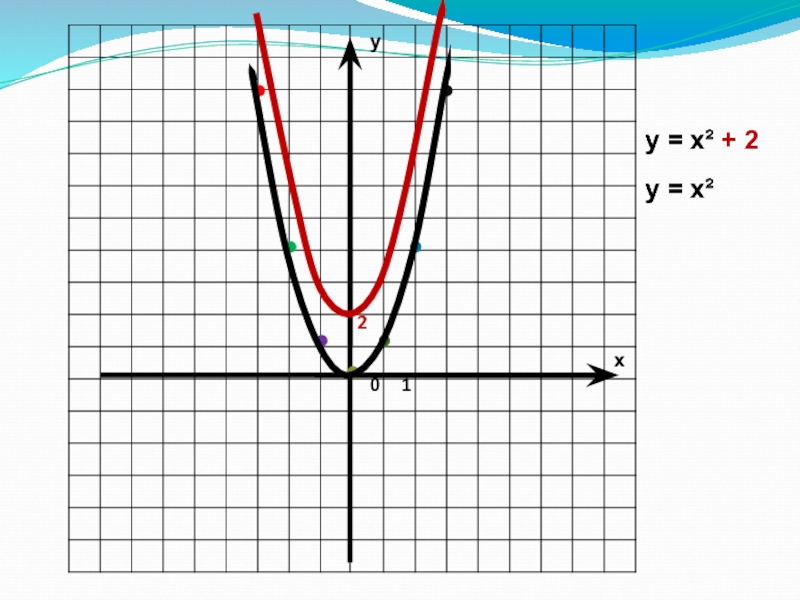
- 10. ух01у = х² + 2у = х² 2
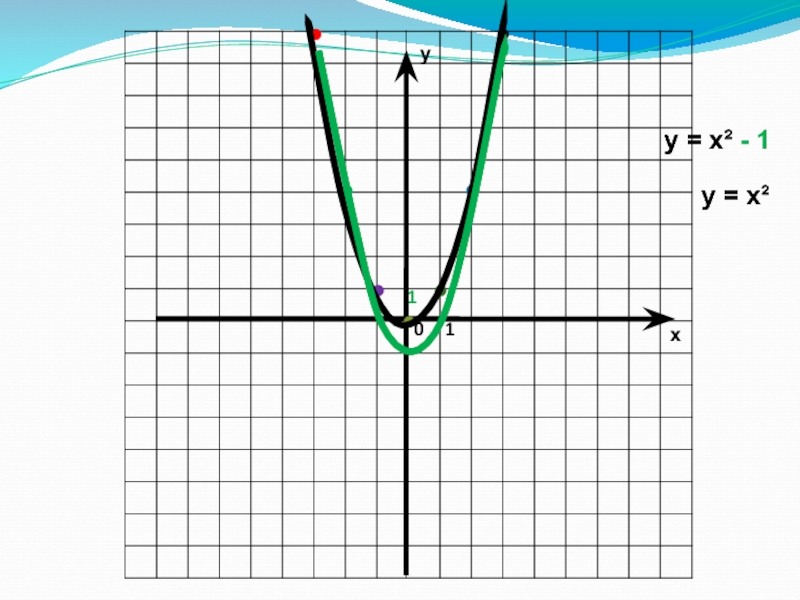
- 11. ух011у = х² - 1у = х²
- 12. у=ax2 +n, a>0 функциясының қасиеттері:1. D(y)=(-∞;+∞(. Функцияның
- 13. у=ax2 +n функциясының графигі у=ax2 +n функциясының
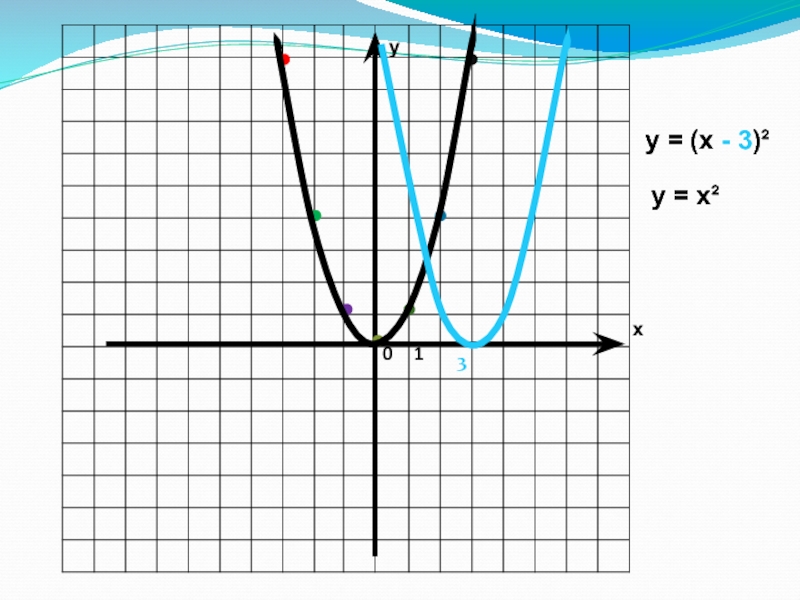
- 14. ух01у = (х - 3)²у = х²3
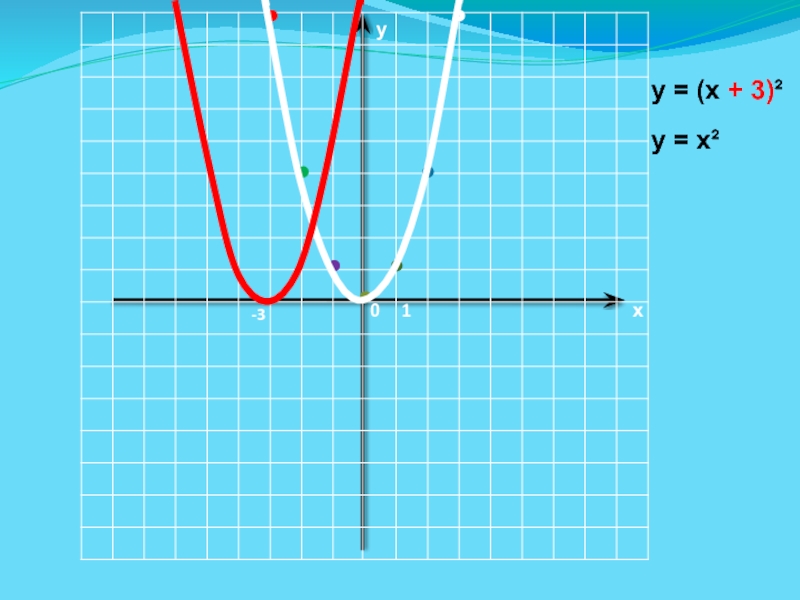
- 15. ух01-3у = (х + 3)²у = х²
- 16. y=a(x-m)2 , a>0 функциясының қасиеттері: 1. D(y)=(-∞;+∞(.
- 17. y=a(x-m)2 функциясының графигі y=a(x-m)2
- 18. Қандай функцияны квадраттық функция деп атайды?
- 19. Берілген функциялардың қайсысы квадраттық
- 20. ТЕСТ
- 21. Т е с тy=x2 функциясының графигін Ох
- 22. Дұрыс жауаптар:1.D 2.А
- 23. “Мен бүгінгі сабақта не үйрендім ?”
- 24. Слайд 24
- 25. Үйге тапсырма:№ 246, 249, № 250
- 26. Назар аударғандарыңызға көп – көп рахмет !
- 27. Скачать презентанцию
Сабақтың мақсаты:Білімділік: y=ах2 функциясының графигінің қасиеттерін пайдалана отырып, у=ах2+n және у=а(х-т)2 функцияларының графиктерін салуға үйрету.Дамытушылық: оқушыларды шапшаңдыққа, тапқырлыққа баулу; логикалық ойлау қабілеттерін жан-жақты дамыту.Тәрбиелік: оқушыларды таза жазуға, сызбаларды ұқыпты орындауға; мәдениетті,
Слайды и текст этой презентации
Слайд 1Математика мұғалімі
Енсегенова Анар Борсакбаевна
Сабақтың тақырыбы: Квадраттық функция.
у=ax2 +n және
y=a(x-m)2
Слайд 2Сабақтың мақсаты:
Білімділік:
y=ах2 функциясының графигінің қасиеттерін пайдалана отырып, у=ах2+n және
у=а(х-т)2 функцияларының графиктерін салуға үйрету.
Дамытушылық:
оқушыларды шапшаңдыққа, тапқырлыққа баулу;
логикалық
ойлау қабілеттерін жан-жақты дамыту.Тәрбиелік:
оқушыларды таза жазуға, сызбаларды ұқыпты орындауға;
мәдениетті, әрі көркем сөйлеуге тәрбиелеу.
Слайд 3
Қайталау сұрақтары:
1. Функцияның берілу тәсілдерін атаңыз.
2. y=ax2 функциясының графигі қандай
фигура және ол қалай аталады?
3. y=ax2 функциясының
a>0 болғандағы негізгі қасиеттері қандай?
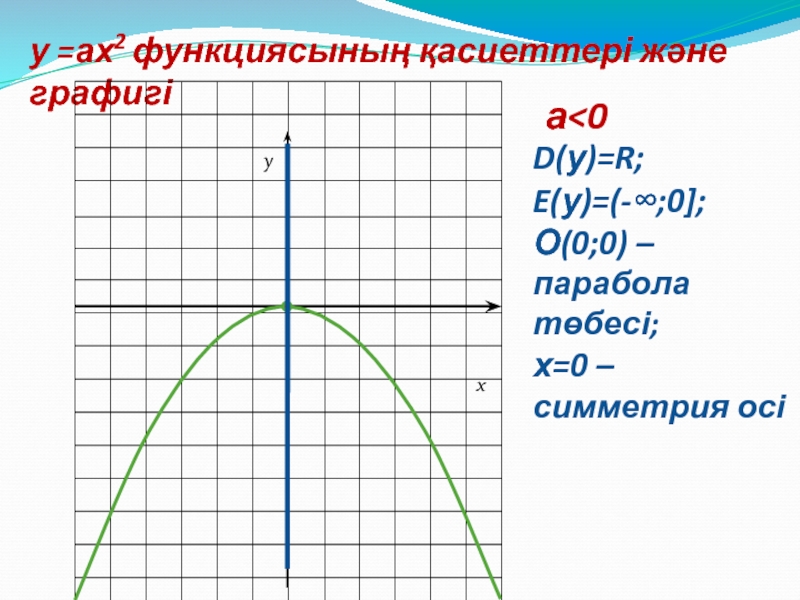
4. y=ax2 (a>0) және y=ax2 (a<0)
функцияларының қандай қасиеттері
ортақ?
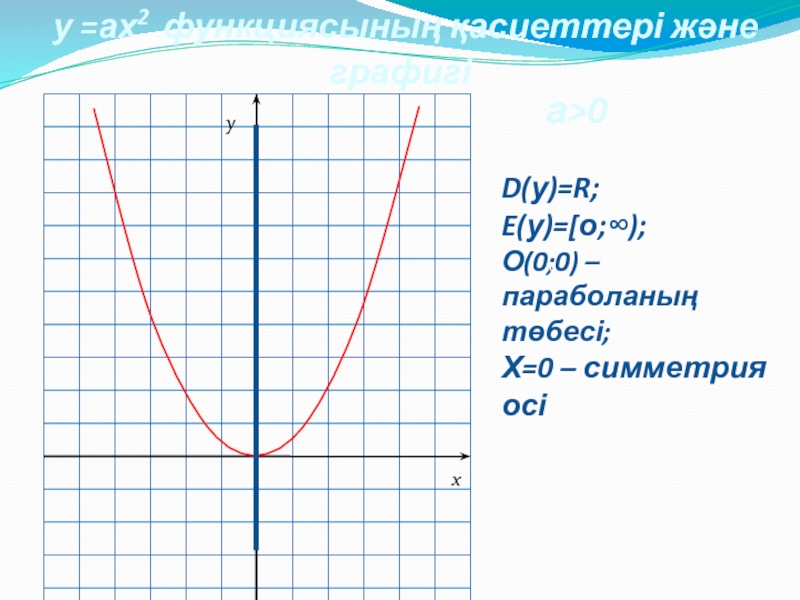
Слайд 4 у =ах2 функциясының қасиеттері және графигі
D(у)=R;
E(у)=[о;∞);
О(0;0) – параболаның төбесі;
Х=0 – симметрия осі
О
у
а>0
х
x
y
Слайд 6у =ах2 + bх + с түріндегі функцияны квадраттық функция
деп атайды,
мұндағы х – тәуелсіз айнымалы,
а, b, және
с –нақты сандар және а ≠ 0.
Квадраттық функцияның графигі парабола болады.
Слайд 9 y=ax2 функциясының графигі арқылы у=ax2 +n және
y=a(x-m)2 функцияларының графиктерін
салуды қарастырамыз.
Слайд 12у=ax2 +n, a>0 функциясының қасиеттері:
1. D(y)=(-∞;+∞(. Функцияның анықталу облысы барлық
нақты сандар жиыны болады.
2. Парабола төбесінің координатасы (о, n).
3. a>0
болғанда параболаның тармақтары жоғары бағытталады. 4. Функцияның графигі Оу осіне қатысты симметриялы болады, х=0 - симметрия осі.
5. Функция (-∞;0) аралығында кемімелі, ал (0;+∞) аралығында өспелі болады.
6. Функцияның ең кіші мәні y= n.
7. E(y)=[ n;+∞) функция мәндерінің жиыны.
Слайд 13у=ax2 +n функциясының графигі
у=ax2 +n функциясының графигі у=ax2 функциясының
графигін ордината осі бойымен n>0 болғанда график n бірлікке жоғары,
ал n<0 болғанда график |n| бірлікке төмен жылжыту арқылы алынған парабола.
Слайд 16y=a(x-m)2 , a>0 функциясының қасиеттері:
1. D(y)=(-∞;+∞(. Функцияның анықталу облысы
барлық нақты сандар жиыны болады.
2. Парабола төбесінің координатасы ( m,
0).3. a>0 болғанда параболаның тармағы жоғары бағытталады.
4. х= m - симметрия осі.
5. Функция (-∞; m) аралығында кемімелі, ал (m; +∞) аралығында өспелі болады.
6. Функцияның ең кіші мәні y= 0.
7. E(y)=[ 0;+∞) функция мәндерінің жиыны.
Слайд 17y=a(x-m)2 функциясының графигі
y=a(x-m)2 функциясының графигі у=ax2
функциясының графигін абсцисса осі бойымен ?>0 болғанда график ? бірлікке
солға қарай, ал ?<0 болғанда график ? бірлікке оңға қарай жылжыту арқылы алынған парабола.
Слайд 19 Берілген функциялардың қайсысы квадраттық функция болады?
1) у=5х2-6
4) у=4х22) у=7х-1 5) у=x3+x+1
3) у=-3х2+х+7 6) у=9х2+4х
Слайд 21Т е с т
y=x2 функциясының графигін Ох осі бойынша 3
бірлікке оңға жылжытқанда алынған параболаның теңдеуін жазыңыз.
А) y=x2-3.
В) y=x2 +3. С) y=(x+3)2 . D) y=(x-3)2 .2. f(x)= х2 -8 квадраттық функциясы берілген. f(3) мәнін табыңыз.
А) 1. В) -2. С) -5. D) 17.
3. y=x2-4 функцияның графигін y=x2 функцияның графигінен қалай алуға болады?
А) 4 бірлік жоғары. В) 4 бірлік төмен. С) 4 бірлік оңға. D) 4 бірлік солға.
4. y=(x+5)2 функцияның графигін y=x2 функцияның графигінен қалай алуға болады?
А) Ох осі бойымен 5 бірлік оңға. В) Ох осі бойымен 5 бірлік солға.
С) Оу осі бойымен 5 бірлік төмен. D) Оу осі бойымен 5 бірлік жоғары.
5. y=(x+5)2 параболасының төбесінің координатасын табыңыз.
А) (-5; 0). В) (5; 0). С) (0; 5). D) (0; -5).







 0 функциясының қасиеттері:1. D(y)=(-∞;+∞(. Функцияның анықталу облысы барлық нақты" alt="у=ax2 +n, a>0 функциясының қасиеттері:1. D(y)=(-∞;+∞(. Функцияның анықталу облысы барлық нақты сандар жиыны болады.2. Парабола төбесінің координатасы">
0 функциясының қасиеттері:1. D(y)=(-∞;+∞(. Функцияның анықталу облысы барлық нақты" alt="у=ax2 +n, a>0 функциясының қасиеттері:1. D(y)=(-∞;+∞(. Функцияның анықталу облысы барлық нақты сандар жиыны болады.2. Парабола төбесінің координатасы">
 0 функциясының қасиеттері: 1. D(y)=(-∞;+∞(. Функцияның анықталу облысы барлық" alt="y=a(x-m)2 , a>0 функциясының қасиеттері: 1. D(y)=(-∞;+∞(. Функцияның анықталу облысы барлық нақты сандар жиыны болады.2. Парабола төбесінің">
0 функциясының қасиеттері: 1. D(y)=(-∞;+∞(. Функцияның анықталу облысы барлық" alt="y=a(x-m)2 , a>0 функциясының қасиеттері: 1. D(y)=(-∞;+∞(. Функцияның анықталу облысы барлық нақты сандар жиыны болады.2. Парабола төбесінің">