в Одессе. Некоторым
учащимся на дом предлагалось творческое
задание: число
3, целое и положительное,изобразить с помощью трех двоек и
математических символов.
То есть любое целое положительное число можно изобразить с помощью трех двоек и математических символов.





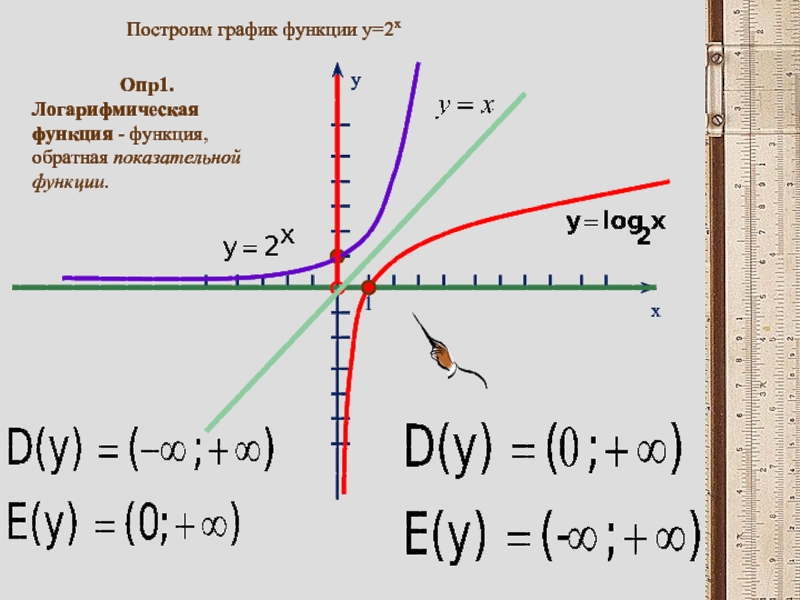
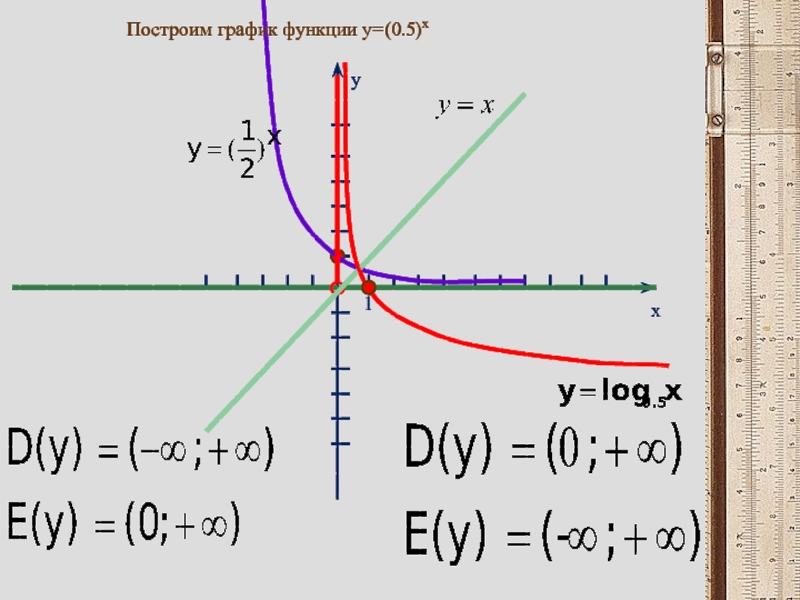
 0," alt="Опр.2Функция вида y = loga х (где а > 0, а ≠ 1) называется логарифмической.">
0," alt="Опр.2Функция вида y = loga х (где а > 0, а ≠ 1) называется логарифмической.">
 11) D(F):(0;+∞)2) не является ни" alt="Свойства функцииСвойства функции y=loga x, при a>11) D(F):(0;+∞)2) не является ни четной, ни нечетной3) возрастает на своей">
11) D(F):(0;+∞)2) не является ни" alt="Свойства функцииСвойства функции y=loga x, при a>11) D(F):(0;+∞)2) не является ни четной, ни нечетной3) возрастает на своей"> 3»" alt="Логарифмическая комедия математический софизм «2>3»">
3»" alt="Логарифмическая комедия математический софизм «2>3»">![Работа в группах№1Найдите наибольшее и наименьшее значение функции на заданном промежутке y=lgx x€ [1;1000]№2 Решите уравнение и](/img/thumbs/9943b8f13663b4770cae7eb3eac0e598-800x.jpg)
![Найти наименьшее и набольшее значении функции на заданном промежуткеy=lgx x€ [1;1000]Решение: функция y=lgx непрерывная и возрастающая.Следовательно своего](/img/thumbs/1a7c0e5d043e06917e61eece76bdc4d9-800x.jpg)
 0 в) lоg4x" alt="Решить уравнения и неравенства а) lоg4x=0; б) lоg4x>0 в) lоg4x">
0 в) lоg4x" alt="Решить уравнения и неравенства а) lоg4x=0; б) lоg4x>0 в) lоg4x"> 0 Ответ : x>1lоg4x" alt="y0 1 2 3 4 5 6 7 8">
0 Ответ : x>1lоg4x" alt="y0 1 2 3 4 5 6 7 8">