Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Логарифмы и логарифмическая функция в природе и технике
Содержание
- 1. Логарифмы и логарифмическая функция в природе и технике
- 2. Цели работы:Закрепить, что такое логарифм и логарифмическая
- 3. Логарифмы и логарифмическая функцияДесятичный логарифм:lg a =
- 4. Логарифмы обладают уникальными свойствами, которые определили их
- 5. Историческая справкаПредшественникиИдейным источником и стимулом применения логарифмов
- 6. Джон Непер и его «удивительная таблица логарифмов»В 1614
- 7. Логарифм данного синуса есть число, которое арифметически
- 8. Дальнейшее развитиеКак вскоре обнаружилось, из-за ошибки в
- 9. Вскоре выяснилось, что место логарифмов в математике
- 10. До конца XIX века общепринятого обозначения логарифма
- 11. Логарифмы вокруг нас
- 12. Магнитуда землетрясения величина, характеризующая энергию, выделившуюся при землетрясении в
- 13. Слайд 13
- 14. Оптическая плотность мера ослабления света прозрачными объектами
- 15. Фотографическая широта характеристика светочувствительного материала(фотоплёнки, передающей телевизионной трубки, матрицы) в фотографии, телевидении и кино.L=lg(H2/H1)=lgH2-lgH1где L — фотографическая широта, Н — экспозиция
- 16. Звезды и шумпо логарифмической шкале. Астрономы делят
- 17. Яркость источников света - шкала звездных величинАстрономы измеряют «блеск»
- 18. Единица громкостиЕдиницей громкости служит «бел», практически -
- 19. Логарифмы «на слуху» и в ухе Когда мы
- 20. Логарифмическая спиральРассматривая устройство уха, можно заметить орган,
- 21. Спирали, встречающиеся в природе, чаще всего бывают логарифмическими. Раковина наутилусаРаковина улиткиСоцветия маргариткиСоцветие подсолнечникаСосновая шишкаПаутина паука Эпейра
- 22. Наиболее впечатляющим примером является спиральная структура галактик.
- 23. Раковины морских животных могут расти лишь в
- 24. Логарифмическая спираль в техникеЛогарифмическая спираль пересекает свои
- 25. Слайд 25
- 26. Логарифмы в химии и биофизикеДля чего же
- 27. Водородным показателем pH называется отрицательный десятичный логарифм концентрации ионов
- 28. Химическая чувствительность — шкала кислотности Первымихимическимииндикаторами былинаши вкусовыерецепторы, которымисегодня пользуютсятолько повара,а раньшеПользовалисьи химики.
- 29. Вычисляем гениев по логарифмической шкалеВоспоминание академика
- 30. Логарифмическая линейка вычисление логарифмов,
- 31. Использование логарифмической линейки в ХХl векеОднако в
- 32. Спасибо за внимание!!!
- 33. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Цели работы:
Закрепить, что такое логарифм и логарифмическая функция
Узнать, как исторически
появилось понятие ЛОГАРИФМ
Узнать применение логарифма и функции в жизни
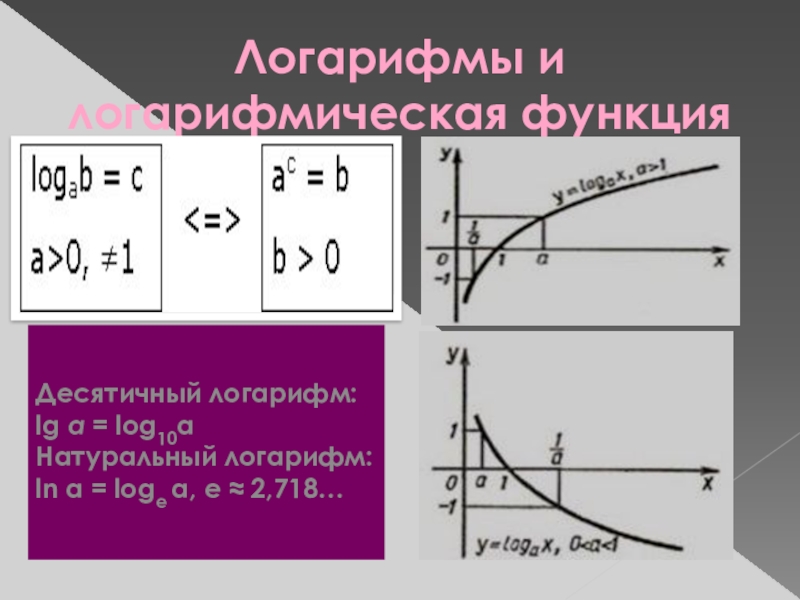
Слайд 3Логарифмы и логарифмическая функция
Десятичный логарифм:
lg a = log10a
Натуральный логарифм:
ln
a = loge a, e ≈ 2,718…
Слайд 4Логарифмы обладают уникальными свойствами, которые определили их широкое использование для
существенного упрощения трудоёмких вычислений
При переходе «в мир логарифмов» умножение заменяется
на значительно более простое сложение, деление — на вычитание, а возведение в степень и извлечение корня преобразуются соответственно в умножение и деление на показательстепени.
Лаплас говорил, что изобретение логарифмов, «сократив труд астронома, удвоило его жизнь»
Слайд 5Историческая справка
Предшественники
Идейным источником и стимулом применения логарифмов послужил тот факт
(известный ещё Архимеду), что при перемножении степеней их показатели складываются:
Индийский математик
VIII века Вирасена, исследуя степенные зависимости, опубликовал таблицу целочисленных показателей (то есть, фактически, логарифмов) для оснований 2, 3, 4
Решающий шаг был сделан в средневековой Европе. Потребность в сложных расчётах в XVI веке быстро росла, и значительная часть трудностей была связана с умножением и делением многозначных чисел, а также извлечением корней. В конце века нескольким математикам, почти одновременно, пришла в голову идея: заменить трудоёмкое умножение на простое сложение, сопоставив с помощью специальных таблиц геометрическую и арифметическую прогрессии, при этом геометрическая
будет исходной.
Тогда и деление автоматически заменяется на неизмеримо более простое и надёжное вычитание, упростятся также возведение в степень и извлечение корня.
Слайд 6Джон Непер и его «удивительная таблица логарифмов»
В 1614 году шотландский математик-любитель Джон Непер опубликовал
на латинском языке сочинение под названием «Описание удивительной таблицы логарифмов»
В
нём было краткое описание логарифмов и их свойств, а также 8-значные таблицы логарифмов синусов, косинусов и тангенсов, с шагом 1'. Термин логарифм, предложенный Непером, утвердился в науке. Теорию логарифмов Непер изложил в другой своей книге «Построение удивительной таблицы логарифмов», , изданной посмертно в 1619 году его сыном Робертом.
Судя по документам, техникой логарифмирования Непер владел уже к 1594 году. Непосредственной целью её разработки было облегчить Неперу сложные астрологические расчёты именно поэтому в таблицы были включены только логарифмы тригонометрических функций.
Понятия функции тогда ещё не было, и Непер определил логарифм кинематически, сопоставив равномерное и логарифмически-замедленное движение; например, логарифм синуса он определил следующим образом
Слайд 7Логарифм данного синуса есть число, которое арифметически возрастало всегда с
той же скоростью, с какой полный синус начал геометрически убывать.
Слайд 8Дальнейшее развитие
Как вскоре обнаружилось, из-за ошибки в алгоритме все значения
таблицы Непера содержали неверные цифры после шестого знака. Однако это
не помешало новой методике вычислений получить широчайшую популярность, и составлением логарифмических таблиц занялись многие европейские математики. Кеплер в изданный им астрономический справочник 1620 года вставил восторженное посвящение Неперу (не зная, что изобретатель логарифмов уже скончался). В 1624 году Кеплер опубликовал свой собственный вариант логарифмических таблиц . Использование логарифмов позволило Кеплеру относительно быстро завершить многолетний труд по составлению Рудольфинских таблиц, которые закрепилиуспех гелиоцентрической астрономии.
Спустя несколько лет после книги Непера появились логарифмические таблицы, использующие более близкое к современному понимание логарифма. Лондонский профессор Генри Бригс издал 14-значные таблицы десятичных логарифмов (1617), причём не для тригонометрических функций, а для произвольных целых чисел до 1000 (7 лет спустя Бригс увеличил количество чисел до 20000). В 1619 году лондонский учитель математики Джон Спайделл переиздал логарифмические таблицы Непера, исправленные и дополненные так, что они фактически стали таблицами натуральных логарифмов. У Спайделла тоже были и логарифмы самих чисел до 1000 (причём логарифм единицы, как и у Бригса, был равен нулю) — хотя масштабирование до целых чисел Спайделл сохранил.
Слайд 9Вскоре выяснилось, что место логарифмов в математике не ограничивается расчётными
удобствами. В 1629 году бельгийский математик Грегуар де Сен-
Венсан показал, что площадь
под гиперболой меняется по логарифмическому закону. В 1668 году немецкий математик Николас Меркатор (Кауфман) открыл и опубликовал в своей книге Logarithmotechnia разложение логарифма в бесконечный ряд. По мнению многих историков, появление логарифмов оказало сильное влияние на многие математические концепции, в том числе:
Формирование и признание общего понятия иррациональных и трансцендентных чисел.
Появление показательной функции и общего понятия числовой функции, числа Эйлера, развитие теории разностных уравнений.
Начало работы с бесконечными рядами.
Общие методы решения дифференциальных уравнений различных типов.
Существенное развитие теории численных методов, требуемых для вычисления точных логарифмических таблиц.
Слайд 10До конца XIX века общепринятого обозначения логарифма не было, основание a указывалось
то левее и выше символа log, то над ним. В конечном
счёте математики пришли к выводу, что наиболее удобное место для основания — ниже строки, после символа log:Краткие обозначения наиболее употребительных видов логарифма —
для десятичного и натурального — появились намного раньше сразу у нескольких авторов и закрепились окончательно также к концу XIX века
Близкое к современному понимание логарифмирования — как операции, обратной возведению в степень — впервые появилось у Валлиса (1685) и Иоганна Бернулли(1694), а окончательно было узаконено Эйлером. В книге «Введение в анализ бесконечных» (1748) Эйлер дал современные определения как показательной, так и логарифмической функций, привёл разложение их в степенные ряды, особо отметил роль натурального логарифма. Эйлеру принадлежит и заслуга распространения логарифмической функции на комплексную область.
Слайд 12Магнитуда землетрясения
величина, характеризующая энергию, выделившуюся при землетрясении в виде сейсмических волн. Первоначальная шкала
магнитуды была предложена американским сейсмологом Чарльзом Рихтером в 1935 году, поэтому в обиходе
значение магнитуды называют шкалой Рихтера.Рихтер предложил для оценки силы землетрясения (в его эпицентре) десятичный логарифм перемещения (в микрометрах) иглы стандартного сейсмографа Вуда-Андерсона
где A — амплитуда колебаний земли (в микрометрах), T — период волны (в секундах), и Q — поправка, зависящая от расстояния до эпицентра D и глубины очага землетрясения h.
Слайд 14Оптическая плотность
мера ослабления света прозрачными объектами (такими, как кристаллы, стекла,
фотоплёнка) или отражения света непрозрачными объектами (такими, как фотография, металлы
и т.д.).Вычисляется как десятичный логарифм отношения потока излучения падающего на объект, к потоку излучения прошедшего через него (отразившегося от него)
К примеру D=4 означает, что свет был ослаблен в 104=10 000 раз, т. е. для человека это полностью чёрный объект, а D=0 означает, что свет прошёл (отразился) полностью.
Слайд 15Фотографическая широта
характеристика светочувствительного материала(фотоплёнки, передающей телевизионной трубки, матрицы) в фотографии, телевидении и кино.
L=lg(H2/H1)=lgH2-lgH1
где L — фотографическая широта, Н — экспозиция
Слайд 16Звезды и шум
по логарифмической шкале. Астрономы делят звезды по степени
яркости на видимые абсолютные звездные величины.
Шум и звёзды объединяются здесь
потому, что громкость шума и яркость звёзд оцениваются одинаковым образом:Звезды первой величины, второй и третьей и т.п. Последовательность видимых звездных величин, которые воспринимались глазом, представляет собой арифметическую прогрессию. Но физическая их яркость изменяется по иному закону:
Яркость звезд составляет геометрическую прогрессию со знаменателем 2,5 легко понять, что «величина» звезды представляют собой логарифм её физической яркости.
Оценивая яркость звезд, астроном оценивает таблицей логарифмов составленной при основании 2,5.
Аналогично оценивается и громкость шума. Вредное влияние промышленных шумов на здоровье рабочих и производстве труда.
Слайд 17
Яркость источников света - шкала звездных величин
Астрономы измеряют «блеск» небесных светил в звездных
величинах
Блеск в астрономии — величина
пропорциональная
логарифму светового потока.
Однако
коэффициент пропорциональности отрицателен (при основании логарифма больше единицы), поэтому самым ярким объектам на небе соответствует большая отрицательная величина (–26,8 для Солнца), а для самых тусклых положительная (28 для едва различимых в телескоп
звезд)
Слайд 18Единица громкости
Единицей громкости служит «бел», практически - его 10 доля,
«децибел». Последовательные степени громкости – 1 бел, 2 бела и
т.д. (практически – 10 децибел, 20 децибел и т.д.) – составляют для нашего слуха арифметическую прогрессию.Физическая же сила этих шумов (точнее - энергия) составляет прогрессию геометрическую со знаменателем 10. Разности громкостей в 1 бел отвечает отношение силы шумов 10. Значит, громкость шума выраженная в белах, равна десятичному логарифму его физической силы.
Слайд 19Логарифмы «на слуху» и в ухе
Когда мы слышим игру музыкальных
инструментов или пение артиста, то вряд
ли задумываемся о природе
звука, положенного в основу любого музыкального действия.Мы слышим звук во время одновременного действия нескольких тонов, частоты которых находятся в простых целочисленных отношениях. Сами звуки различаются по высоте, которая зависит от частоты колебаний струны. Для того чтобы понять, как человек ощущает звук, надо начать с описания уха
1 — наружный слуховой проход; 2 — барабанная перепонка; 3 — полость среднего уха (барабанная полость); 4 — молоточек; 5 — наковальня; 6 — стремечко; 7 — полукружные каналы; 8 — преддверие; 9 — улитка; 10 — овальное окно; 11 — евстахиева труба.
Слайд 20Логарифмическая спираль
Рассматривая устройство уха, можно заметить орган, который называется улиткой.
Название вполне оправдано, так как форма этой части действительно напоминает
улитку. Она напоминает спирально закрученную трубку. Контур «улитки» можно соотнести с логарифмической спиралью в математике.У логарифмической спирали все время выдерживается постоянный угол относительно оси (раковина улитки)
Первым ученым, открывшим эту удивительную кривую, был Рене Декарт (1596—1650)
Слайд 21Спирали, встречающиеся в природе, чаще всего бывают логарифмическими.
Раковина наутилуса
Раковина
улитки
Соцветия маргаритки
Соцветие подсолнечника
Сосновая шишка
Паутина паука Эпейра
Слайд 22Наиболее впечатляющим примером является спиральная структура галактик. И этот факт
представляет не меньшую загадку, чем проблема их строения. Галактики состоят
из горячих звезд и скоплений газа, которые в результате вращения галактика распределяются вдоль ветвей логарифмической спирали. У центра галактики ветви спирали вращаются быстрее, чем на границе, то есть они должны были бы быстро раскручиваться, и даже уничтожиться. Однако галактики, как правило, сохраняют спиральную структуру, что говорит о том, что ветви вовсе не раскручиваются.Слайд 23Раковины морских животных могут расти лишь в одном направлении. Чтобы
не слишком вытягиваться им приходиться скручиваться, причём каждый следующий виток
подобен предыдущему. А такой рост может совершаться лишь по логарифмической спирали, можно сказать что эта спираль является математическим символом соотношения форм роста. Поэтому раковины многих моллюсков, улиток, а так же рога таких млекопитающих как архары (горные козлы), закручены по логарифмической спирали.Слайд 24Логарифмическая спираль в технике
Логарифмическая спираль пересекает свои радиус-векторы под постоянным
углом. На основании этого ее называют равноугольной.
Это свойство находит
свое применение в технике. Дело в том, что в технике часто применяются вращающиеся ножи. Сила с которой они давят на разрезаемый материал, зависит от угла резания, т.е. угла между лезвием ножа и направлением скорости вращения. Для постоянного давления нужно, чтобы угол резания сохранял постоянное значение, а это будет в том случае, если лезвия ножей очерчены по дуге логарифмической спирали. Величина угла резания зависит от обрабатываемого материала.В гидротехнике по логарифмической спирали изгибают трубу, проводящую поток воды к лопастям турбины. Благодаря такой форме трубы потери энергии на изменение направления течения в трубе оказываются минимальными и напор воды используется с максимальной производительностью.
Нажимая на клавиши современного рояля, мы, можно сказать, играем на логарифмах.
Слайд 25 Никогда еще в природе не существовало столь совершенного примера логарифмических
спиралей…)
Логарифмические линии в природе замечают не только математики, но и
художники, например, этот вопрос чрезвычайно волновал Сальвадора Дали. картина Вермера «Кружевница»
Слайд 26Логарифмы
в химии и биофизике
Для чего же нужны логарифмы в химии
и как они применяются? Думаю, все из нас неоднократно встречались с
пометкой pH на моющих средствах. В химии эту пометку принято называть водородным показателем.ЗА ЧТО ЖЕ ОН ОТВЕЧАЕТ?
Слайд 27Водородным показателем pH называется отрицательный десятичный логарифм концентрации ионов водорода.
Переводя на доступный
язык, можно сказать, что с помощью водородного показателя определяется уровень
кислотности среды.Слайд 28
Химическая чувствительность — шкала кислотности
Первыми
химическими
индикаторами были
наши вкусовые
рецепторы, которыми
сегодня пользуются
только повара,
а раньше
Пользовались
и химики.
Слайд 29
Вычисляем гениев по логарифмической шкале
Воспоминание академика В. Л. Гинзбурга: «… Ландау имел
«шкалу заслуг» в области физики. Шкала была логарифмическая (классу 2 отвечали
достижения в 10 раз меньше, чем для класса 1). Из физиков нашего века класс 0,5 имел только Эйнштейн, к классу 1 относились Бор, Дирак, Гейзенберг и ряд других…»Остается неясным,
логарифм по какому
основанию — 10 или
2,512… — использовал
Лев Ландау для
определения уровня
гениальности физиков-
теоретиков. Несомненно
лишь одно: для этих
сугубо эмоциональных,
субъективных оценок
он использовал логарифмическую шкалу.
Слайд 30 Логарифмическая линейка вычисление логарифмов, тригонометрических функций и других— аналоговое вычислительное
устройство, позволяющее выполнять несколько математических операций, в том числе, умножение
и деление чисел, возведение в степень (чаще всего в квадрат и куб) и вычисление квадратных и кубических корней и операции.Слайд 31Использование логарифмической линейки в ХХl веке
Однако в начале XXI века
логарифмические
линейки получили
второе рождение в наручных часах. Дело в том,
что следуя модепроизводители дорогих и
престижных марок часов перешли
от электронных хронометров с ЖК-
экранами к стрелочным и
соответственно места для
встраиваемого калькулятора
оказалось недостаточно.
Однако
спрос на хронометры со
встроенным вычислительным
устройством среди следящих за
модой людей заставил
производителей часов выпустить
модели с встроенной логарифмической линейкой выполненной в виде вращающихся колец со шкалами вокруг циферблата.