Математика в архитектуре и живописи

г.Перми
Окунев Александр
Руководитель Кузьменкова Н.Я.
«Всё прекрасно благодаря числу».Пифагор
«Умеренность и

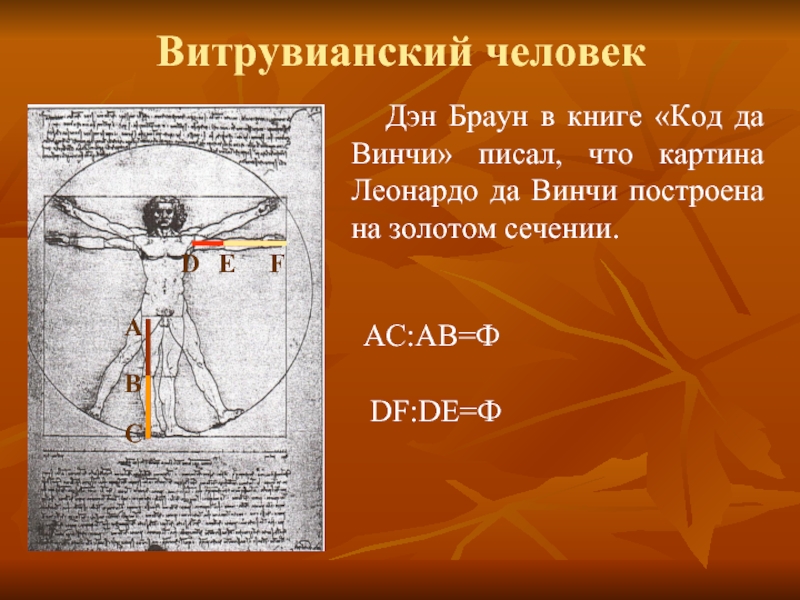
Математика играет в архитектуре и живописи очень важную роль, а именно: архитекторы и художники используют математические законы гармонии, симметрию и пропорции, в основном золотое сечение, при создании своих работ.

длина меньшей части относится к длине большей части так же,

A

B

C

φ≈0,62 Ф=1/φ ≈ 1,618

Ряд золотого сечения является геометрической прогрессией

Свойство ряда золотого сечения

Золотые фигуры

Золотыми фигурами называются такие фигуры, стороны которых находятся в золотом соотношении

M

N

P

Q

Золотой прямоугольник

MN:NP=φ

A

B

C

Золотой треугольник

BC:AB=φ

А математика – это универсальный язык науки, поэтому мы можем

А.В. Волошинов

«Всё вокруг – геометрия.
Дух геометрического и математического порядка станет властителем архитектурных судеб»

Ле Корбюзье

сооружений мира. Храм был возведён при Перикле в Vв. до

лежит золотое сечение.
Жолтовский писал, что высоты поддерживающих (ВС) и поддерживаемых

AC:BC=φ

Хэмбидж разбил фасад Парфенона на квадраты и прямоугольники, стороны которых относятся, как 1 к √5.
Легко видеть, что главные вертикальные размеры храма соотносятся в золотой пропорции (см. рисунок)

Золотая пропорция на фасаде Парфенона

Линейчатыми называются поверхности, образованные движением прямой в пространстве.
К ним относятся

Цилиндрические своды сооружали в Древнем Риме. Позже математики открыли ещё 2 вида линейчатых поверхностей: гиперболический параболоид и однополостный гиперболоид. Они образованы двумя семействами прямых в пространстве

гиперболических параболоидов открыл испанский архитектор Феликс Кандела. Он показал их

один из величайших памятников архитектуры ранней готики.
Огюст

форм и лаконичность украшений, храм Покрова на Нерли считается одной

В основе храма лежит золотое сечение

Ряд золотого сечения:

картины к её ширине равно φ. Расстояние от левого края

На рисунке показано, что колени делят тело, пупок – туловище, брови – лицо в золотом сечении.

прямоугольниках

писал, что картина Леонардо да Винчи построена на золотом сечении.
A
B
C
D
E
F
AC:AB=Ф
DF:DE=Ф

фракталы, тесселляции, невозможные фигуры и искажённые перспективы.
Иштван Орос «Перекрёстки»
Невозможные

что волна является фрактальной тесселяцией, которая состоит из рыб разных