Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Методические особенности работы в профильных классах
Содержание
- 1. Методические особенности работы в профильных классах
- 2. Как сделать урок более продуктивным и интересным,
- 3. В последнее время в старшей школе приоритетным
- 4. Хорошо усвоить знания можно, если изучать на
- 5. Урок лекция состоит из трех этапов:1.Организационный момент;
- 6. 1. Лекция – 3ч- показательная функция;- показательные
- 7. 1.Введение определения показательной функции;2.Графики показательной функции;3.Свойства показательной
- 8. Тип лекции: лекция-диалог, т.е. содержание лекции подается
- 9. Целеполагание может быть следующим.Например, рассмотрим функции:y=x2, y=2x,
- 10. Сравниваем по основанию функции:-+--
- 11. Показательная функцияy=ax (a>0, a1)D (y) = RE (y)=(0;+∞)a>1, y возр. на R
- 12. ЛЕКЦИЯ № 2 « ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ И НЕРАВЕНСТВА»
- 13. Лекция №3«Методы решения показательных уравнений и неравенств,
- 14. Вывод: составление учителем детального плана, логически стройное
- 15. За счёт сокращения времени на формирование знаний
- 16. Индивидуально - исследовательский метод Исследовательский метод определяется
- 17. Формы задания при исследовательском методе могут быть
- 18. Характерные особенности урока - исследования
- 19. Структура урока -исследования
- 20. Урок «Исследование логарифмического уравнения»Тип урока:Исследовательская работаЦель:Формирование умений
- 21. ЗаданиеПри каких значениях а сумма равна 1 хотя бы при одном значении х ?
- 22. I Группа Поставьте задачу, которую необходимо
- 23. II ГруппаГруппу составляют учащиеся с выше средними
- 24. III Группа. Группу составляют учащиеся со средними
- 25. IV Группа. Группу составляют учащиеся с низкими
- 26. Анализ результатов решения предложенного задания по группам.
- 27. Рефлексия (самооценка).Каждый ученик получает карточки с критериями
- 28. Слайд 28
- 29. Уроки обобщения часто устраиваю в форме презентаций
- 30. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1 Методические особенности обучения математике
в профильных классах
Захаренко Елена Леонидовна, учитель
математики
Слайд 2Как сделать урок более продуктивным и интересным, какие формы и
методы нужно применить, чтобы дети хорошо усваивали материал? Этот вопрос
интересует любого учителя.Формы обучения- способы организации учебного процесса.
Методы обучения - упорядоченный комплекс дидактических приемов и средств, посредством которых реализуются цели обучения.
Слайд 3В последнее время в старшей школе приоритетным является профильное обучение.
Одним из факторов, определяющих содержание профильного обучения, является то, чтобы
подготовить выпускников к ЕГЭ. Поэтому учителям, работающим в профильных классах нужно так организовать и направить процесс обучения, чтобы повысить надежность передаваемой информации, улучшить прочность запоминания материала.
Слайд 4Хорошо усвоить знания можно, если изучать на малом интервале времени
(1-2 урока) группы понятий, преобразований, определений, связанных друг с другом
по форме и содержанию, т.е. осуществлять передачу информации крупными блоками. Такой опыт обучения приносит 20 % чистой экономии времени против общепринятых учебных норм.Поэтому, в классах, где математика является профильным предметом, предлагаем изучать теоретический материал крупными блоками и осуществлять это в форме урока-лекции.
Слайд 5
Урок лекция состоит из трех этапов:
1.Организационный момент; обсуждение плана лекции.
2.Содержание
лекции (2/3 урока)
3.Ответы на вопросы; обобщение, выводы; постановка домашнего задания
Слайд 61. Лекция – 3ч
- показательная функция;
- показательные уравнения и неравенства;
-
методы решения (уравнений, неравенств, систем);
2. Семинар – 1ч
Практикум
– 3чУрок-исследование – 1ч;
3. Обобщающий урок – 1ч;
4. Контрольная работа – 1ч;
Тема «Показательная функция»
(10 класс-10 ч.)
Слайд 71.Введение определения показательной функции;
2.Графики показательной функции;
3.Свойства показательной функции;
4.Показательная функция в
физике, биологии, экономике (беседа);
План по теме
ЛЕКЦИЯ
№ 1 «Показательная функция» Слайд 8Тип лекции: лекция-диалог, т.е. содержание лекции подается через серию вопросов,
на которые ученик отвечает непосредственно в ходе лекции.
Цель урока-лекции: ознакомиться
с понятием показательная функция; рассмотреть ее свойства; научиться строить графикПредполагаемое время: 45 минут
Оборудование: 1) План лекции
2) опорный конспект
3) Проектор со слайдами
Слайд 9Целеполагание может быть следующим.
Например, рассмотрим функции:
y=x2, y=2x, y=(1/5)x, y=x1/5, y=3x,
y=x3
Назовите известные вам функции.
Какие новые для вас функции? ( y=2x,
y=(1/5)x, y=3x)Именно сегодня на уроке мы и будем изучать эти функции.
Слайд 13Лекция №3
«Методы решения показательных уравнений и неравенств, систем»
(перечисление примеров без
решения)
1)Приведение обеих частей уравнения (неравенства) к одному основанию: 42х=1; (1/2)x>16
2)
Замена неизвестного: 4х+92х=10; 16х+4х-2>03) Логарифмирование по удобному основанию: х2+log3x=38
4) Графический способ решения:
76-х=х+2
5) Приведение обеих частей к одному показателю:
62х+4=33х 2х+8
Слайд 14Вывод: составление учителем детального плана, логически стройное и последовательное изложение
изучаемого материала крупными блоками , обобщающие выводы, живой язык, контакт
с аудиторией, оптимальный темп изложения , использование наглядности, составление конспекта делает учебный процесс более эффективным.А так же повышается качество знаний. Так за контрольную работу по этой теме в моём классе из 24 человек справились на «5» - 7 человек, на «4» - 11, и на «3» - 6 человек, что позволяет сделать вывод о сформированности умений.
Слайд 15За счёт сокращения времени на формирование знаний увеличивается время на
формирование умений и навыков. В результате остаётся время на применение
знаний в нестандартных ситуациях, т.е. на урок – исследование.Слайд 16Индивидуально - исследовательский метод
Исследовательский метод определяется как самостоятельное решение
учащимися новой для них проблемы с применением таких элементов научного
исследования, как наблюдение и самостоятельный анализ фактов, выдвижение гипотезы и ее проверка, формирование вывода. Применение исследовательского метода возможно в ходе решения сложной задачи, анализа информации из учебника и др.источников, разрешения поставленной учителем проблемы.Слайд 17Формы задания при исследовательском методе могут быть различными: поддающиеся быстрому
решению, требующие целого урока, домашнее задание на определенный срок. Обязательным
элементом занятий является работа в группах с последующей презентацией ее результатов всем учащимся.Учебное исследование является основой для проведения нетрадиционных уроков: урок-исследование, урок-творческий отчет, урок-защита исследовательского проекта.Слайд 20Урок «Исследование логарифмического уравнения»
Тип урока:
Исследовательская работа
Цель:
Формирование умений решать логарифмические уравнения
с параметрами; умение самостоятельно проводить исследования.
Организационный момент.
Учитель формирует задачу, поясняет
актуальность задачи, обоснование данного исследования. Учитель рассказывает о пользе данного исследования с позиции приобретения новых знаний, практики. Учитель проводит инструктаж, выдает каждой группе карточку с задачей и карточку предписаний.Слайд 22
I Группа
Поставьте задачу, которую необходимо решить.
Обозначьте проблему исследования (сформулируйте
самостоятельно).
Выполните сбор фактического материала, для этого решите две частные задачи.
Выполните
поставленную задачу.Сформулируйте вывод.
Группу составляют учащиеся с высокими учебными возможностями. В карточке предписаний для группы записаны только этапы исследовательской деятельности.
Слайд 23II Группа
Группу составляют учащиеся с выше средними учебными возможностями. Раздается
карточка предписаний, где проблема формируется учителем.
Поставьте задачу, которую необходимо решить.
Проблема,
над которой вы должны работать: найти значение а, при которой уравнение имеет хотя бы один корень.
Выполните сбор фактического материала, для этого решите две частные задачи.
Выполните поставленную задачу по плану:
а) Произведите замену переменных;
б) Определите область определения полученного уравнения;
в) Решите уравнение.
Сформулируйте вывод
Слайд 24III Группа. Группу составляют учащиеся со средними учебными возможностями.
Поставьте
задачу, которую необходимо решить.
Проблема, над которой вы должны работать: найти
значение а, при которой уравнение имеет хотя бы один корень.Выполните сбор фактического материала, для этого решите две частные задачи, самостоятельно выбрав значение а.
Выполните поставленную задачу по плану ( вставьте пропуски)
а) Произведите замену переменных:
б) Уравнение примет вид:
в) ООУ:
г)
(y-1)(y-7)=____;
____+7-a=0;
D=________;
Вывод.
Заметим, что корень y=_____ удовлетворяет условию y>7 при всех a>0. Значит, решением является _______
Слайд 25IV Группа. Группу составляют учащиеся с низкими учебными возможностями
Поставьте задачу,
которую необходимо решить.
Проблема, над которой вы должны работать. Найти значение
а, при которой уравнение имеет хотя бы один кореньВыполните сбор фактического материала, для этого решите две частные задачи по плану:
Составьте логарифмическое уравнение при a=16;
Выполните необходимые преобразования логарифмического уравнения;
Произведите замену
Выполните преобразование и решите квадратное уравнение;
Найдите корни логарифмического уравнения;
Составьте логарифмическое уравнение, самостоятельно выбрав значение a, и решите его по заданному плану.
Выполните поставленную задачу по плану (вставьте пропуски):
а)Произведите замену переменных:
б) Уравнение примет вид:
в)ООУ:
(y-1)(y-7)=____;
____+7-a=0;
D=________;
Вывод.
Заметим, что корень y=_____ удовлетворяет условию y>7 при всех a>0. Значит, решением является _______
Слайд 26Анализ результатов решения предложенного задания по группам. Учащиеся формулируют проблему
исследования предложенного задания. Из каждой группы приглашается один ученик, предлагается
начать обсуждение решения задачи частных случаев: в группах II и III решение задачи при самостоятельно выбранном значении а; в IV в группе рассматривается решение задачи при а=16.; Iгруппа показывает решение в общем виде.Слайд 27Рефлексия (самооценка).
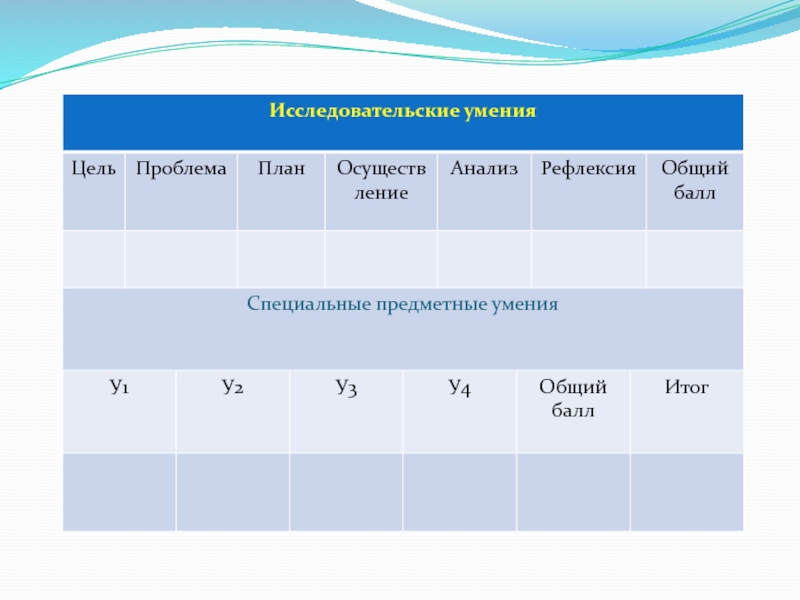
Каждый ученик получает карточки с критериями исследовательской работы. Если
ученик не справляется с выполнением I этапа «Исследовательские умения», или
с каким то его пунктом, то учитель ему в этом помогает или предлагает готовые формулировки , что учитывается при выставлении баллов. Каждое умение оценивается от 0 до 5 баллов .«Специальные умения» ученик выполняет самостоятельно.
У1-умение применять свойство лагорифмов;У2-умение решать показательные уравнения;У3-умения решать квадратные уравнения;У4-умение производить выборку корней.