Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Методы решения тригонометрических уравнений (10 класс)
Содержание
- 1. Методы решения тригонометрических уравнений (10 класс)
- 2. «Считай несчастным тот день или тот
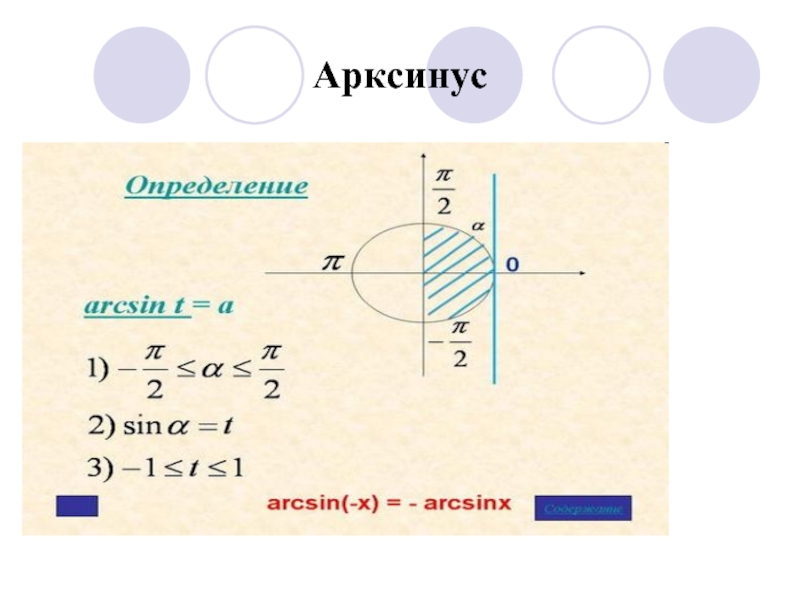
- 3. Арксинус
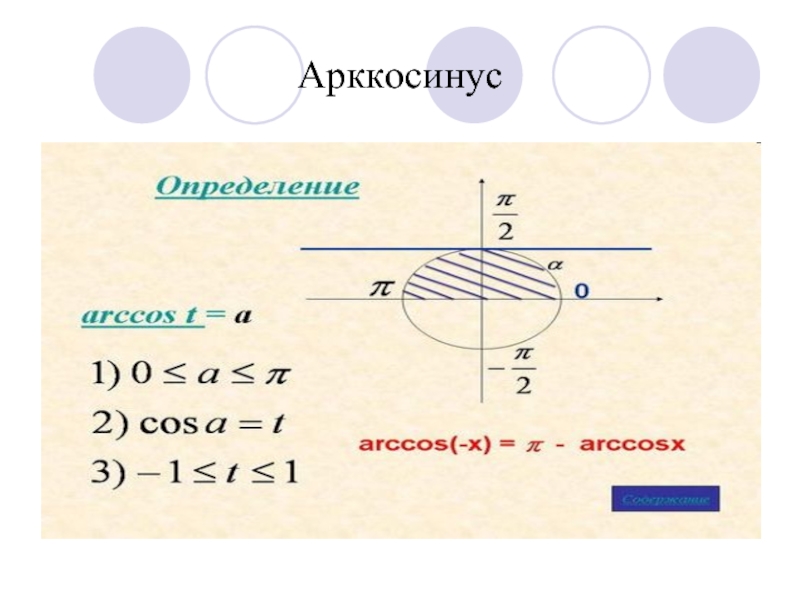
- 4. Арккосинус
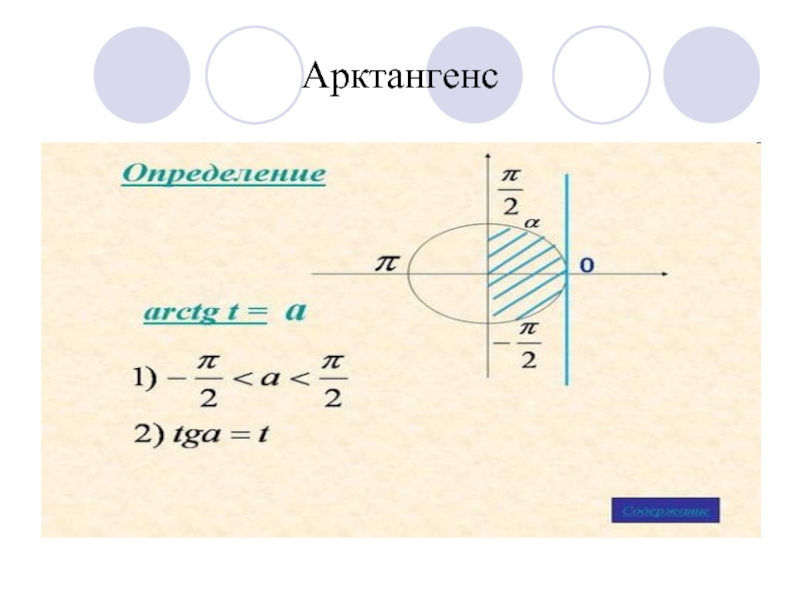
- 5. Арктангенс
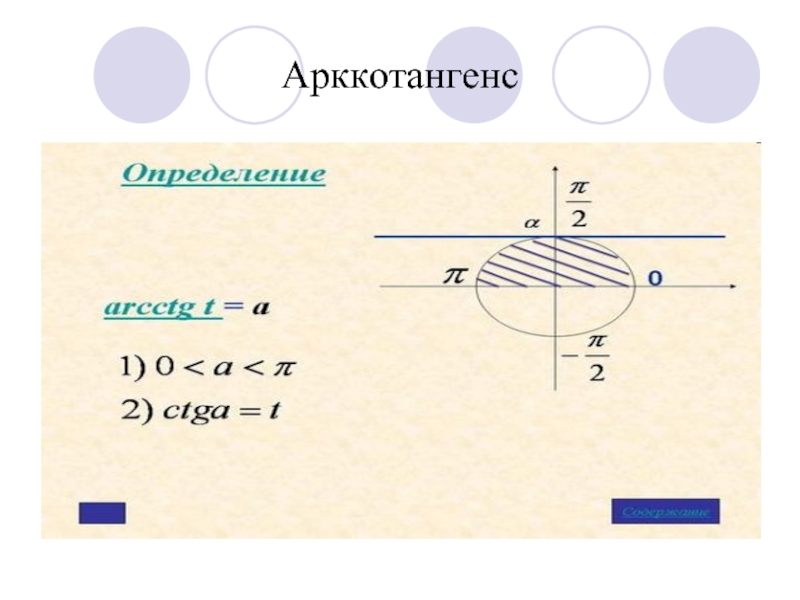
- 6. Арккотангенс
- 7. Финк- Райт – Раунд - Робинarcsin √2/2arccos 1arcsin (- 1/2 )arccos (- √3/2)arctg √3
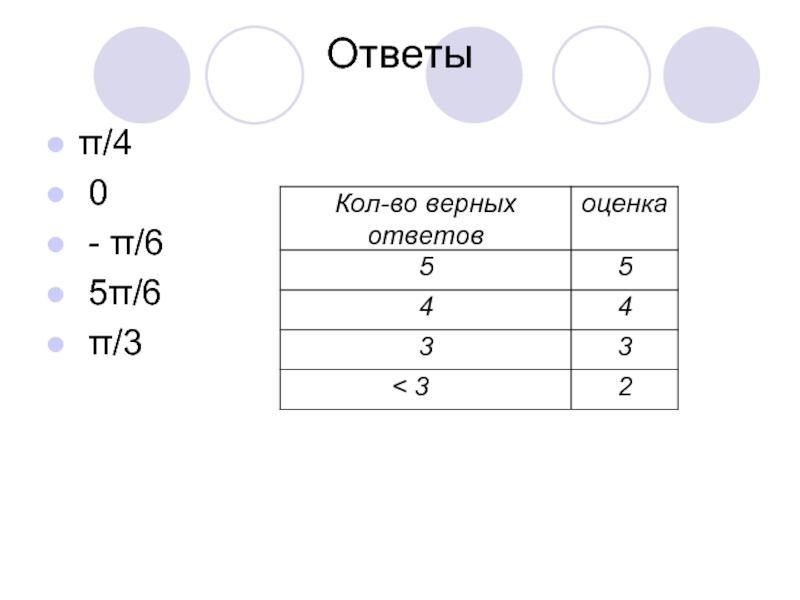
- 8. Ответыπ/4 0 - π/6 5π/6 π/3
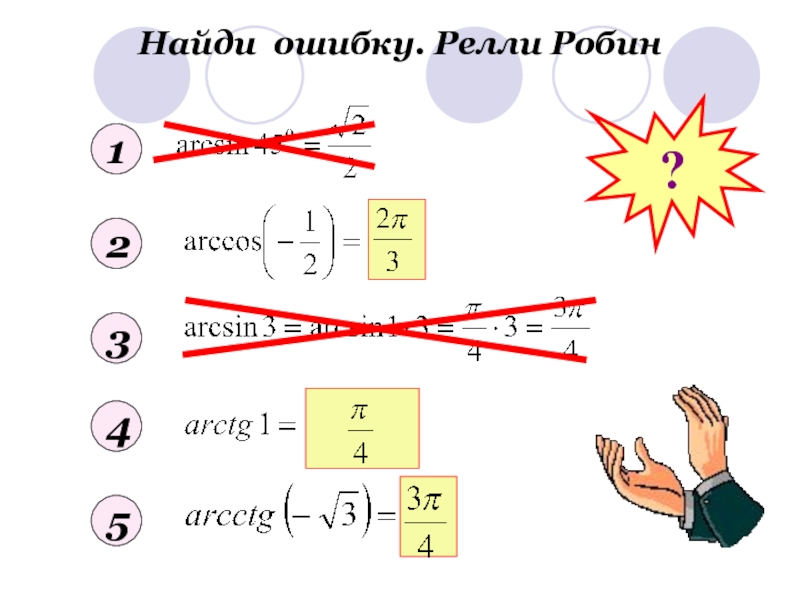
- 9. Найди ошибку. Релли Робин12345?
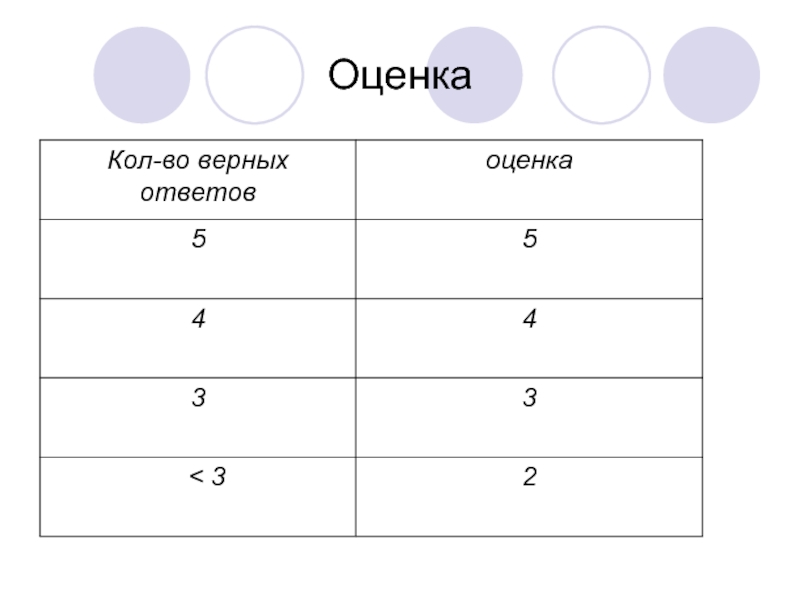
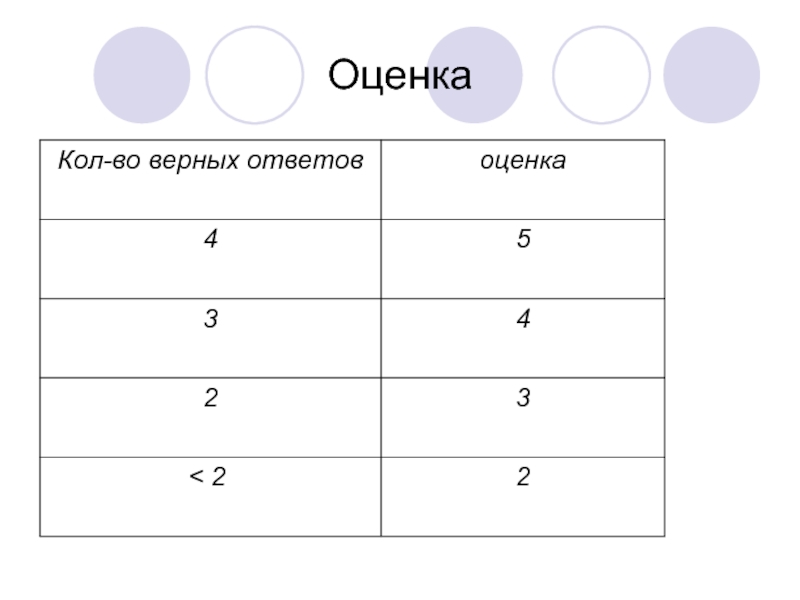
- 10. Оценка
- 11. Общая схема исследования функции1. Область определения функции.2.
- 12. Функция у = sin x.1. Областью определения
- 13. Функция у = соs x.1. Областью определения
- 14. Функция у = tg x1. Областью определения
- 15. Функция у = ctg x1. Областью определения
- 16. Клок БадисПример 1Пример 1. sin
- 17. Пример 1 sin x = −
- 18. Пример 2 cos x =
- 19. Пример 3 tg x = −
- 20. Пример 4 сtg x =
- 21. Оценка
- 22. Другие тригонометрические уравнения1.Сводимые к квадратным
- 23. Содержание Метод замены переменной Метод разложения на множителиС помощью тригонометрических формул:Формул сложенияФормул приведенияФормул двойного аргумента
- 24. Основные методы решения тригонометрических уравнений. Домашнее
- 25. « То, что мы знаем, -
- 26. Спасибо!
- 27. Билетик на выхода)2 cos2х + 5 sin
- 28. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1
Обобщающий урок по теме:
«Методы решения тригонометрических уравнений»
10 класс
Горбунова Вера
Александровна, учитель физики и математики
РТСлайд 2 «Считай несчастным тот день или тот час, в который
ты не усвоил ничего нового и ничего не прибавил к
своему образованию»Я. А. Коменский
Слайд 11Общая схема исследования функции
1. Область определения функции.
2. Исследование области значений
функции
3. Исследование функции на четность.
4.. Исследование функции на периодичность
5.
Формулы корней тригонометрических уравнений.Слайд 12Функция у = sin x.
1. Областью определения функции является множество
всех действительных чисел ( R )
2. Областью значений)
- [ - 1; 1 ].3. Функция у = sin α нечетная, т.к. sin (- α) = - sin α
4. Функция периодическая, с главным периодом 2π
sint = а, где | а |≤ 1
1)sint=0
t = 0+πk‚ kЄZ
2)sint=1
t = π/2+2πk‚ kЄZ
3)sint = - 1
t = - π/2+2πk‚ kЄZ
Слайд 13Функция у = соs x.
1. Областью определения функции является множество
всех действительных чисел ( R )
2. Областью изменений
(Областью значений) - [ - 1; 1 ]3. Функция у = cos α четная, т.к. cos (- α) = cos α
4. Функция периодическая, с главным периодом 2π.
cost = а , где |а| ≤ 1
1)cost=0
t = π/2+πk‚ kЄZ
2)cost=1
t = 0+2πk‚ kЄZ
3)cost = -1
t = π+2πk‚ kЄZ
Слайд 14Функция у = tg x
1. Областью определения функции является множество
(- π/2; π/2)
2. Областью значений R.
3.Функция у = tg x
нечетная, т.к. tg (- α) = - tg α4. Функция периодическая, с главным периодом π.
tgt = а, аЄR
t = arctg а + πk‚ kЄZ
Слайд 15Функция у = ctg x
1. Областью определения функции является множество
(πn; π + πn)
2. Областью значений R
3. Функция у
= ctg x нечетная, т.к. ctg (- α) = - ctg α4. Функция периодическая, с главным периодом π.
ctgt = а, аЄR
t = arcctg а + πk‚ kЄZ
Слайд 16Клок Бадис
Пример 1Пример 1. sin x = −
Пример
2Пример 2. cos x =
Пример 3Пример 3.
tg x = − 1Пример 4Пример 4. ctg x =
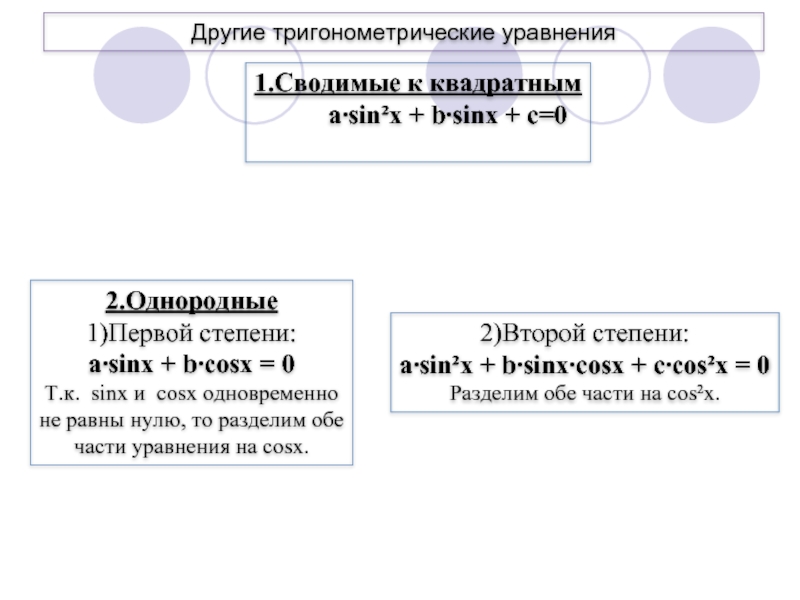
Слайд 22Другие тригонометрические уравнения
1.Сводимые к квадратным
a∙sin²x
+ b∙sinx + c=0
2.Однородные
1)Первой степени:
a∙sinx + b∙cosx = 0
Т.к.
sinx и cosx одновременноне равны нулю, то разделим обе
части уравнения на cosx.
2)Второй степени:
a∙sin²x + b∙sinx∙cosx + c∙cos²x = 0
Разделим обе части на cos²x.
Слайд 23Содержание
Метод замены переменной
Метод разложения на множители
С помощью тригонометрических
формул:
Формул сложения
Формул приведения
Формул двойного аргумента
Слайд 24Основные методы решения тригонометрических уравнений.
Домашнее задание.
На «3»
1) 3 sin
x+ 5 cos x = 0
2) 5 sin2 х -
3 sinх cos х - 2 cos2х =0 На «4»
1) 3 cos2х + 2 sin х cos х =0
2) 5 sin2 х + 2 sinх cos х - cos2х =1
На «5»
1) 2 sin x - 5 cos x = 3
2) 1- 4 sin 2x + 6 cos2х = 0
На «3»
1) cos x+ 3 sin x = 0
2) 6 sin2 х - 5 sinх cos х + cos2х =0
На «4»
1) 2 sin2 x – sin x cosx =0
2) 4 sin2 х - 2sinх cos х – 4 cos2х =1
На «5»
1) 2 sin x - 3 cos x = 4
2) 2 sin2 х - 2sin 2х +1 =0