Слайд 1Многогранники
Учитель математики МБОУ «Школа № 15»
Болгова Г.А.
Слайд 2Понятие многогранника.
Поверхность, составленную из многоугольников и ограничивающую некоторое геометрическое тело
называют многогранной поверхностью или многогранником.
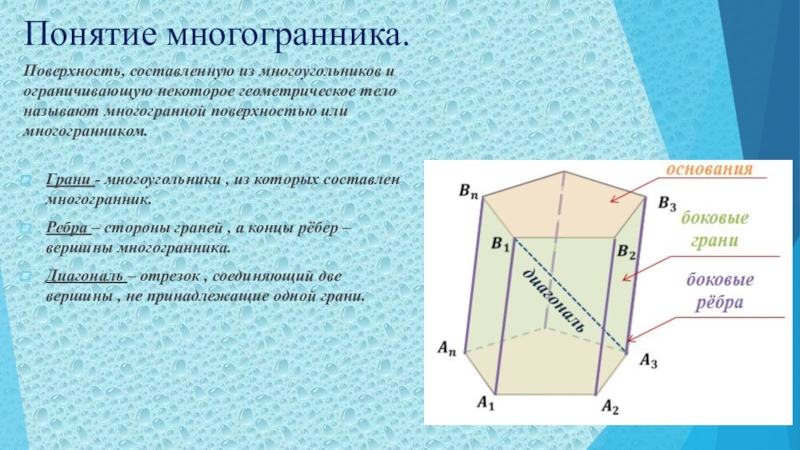
Грани - многоугольники , из которых
составлен многогранник.
Ребра – стороны граней , а концы рёбер – вершины многогранника.
Диагональ – отрезок , соединяющий две вершины , не принадлежащие одной грани.
Слайд 3Давайте рассмотрим, например, прямоугольный параллелепипед: ABCDA1B1C1D1. поверхность прямоугольного параллелепипеда состоит
из 6 прямоугольников. Т.е. его поверхность составлена из шести многоугольников. Многоугольники,
из которых составлен многогранник, называют его гранями.
Заметим, что никакие две соседние грани многогранника не лежат в одной плоскости.
Стороны граней называются ребрами многогранника. А концы ребер вершинами многогранника.
Отрезок, соединяющий две вершины, не принадлежащие одной грани, например, A1C – называется диагональю многогранника. В данном случае, диагональ прямоугольного параллелепипеда.
Плоскость, по обе стороны от которой имеются точки многогранника, называется секущей плоскостью, а общая часть многогранника и секущей плоскости – сечением многогранника.
Слайд 4Выпуклые и невыпуклые многогранники
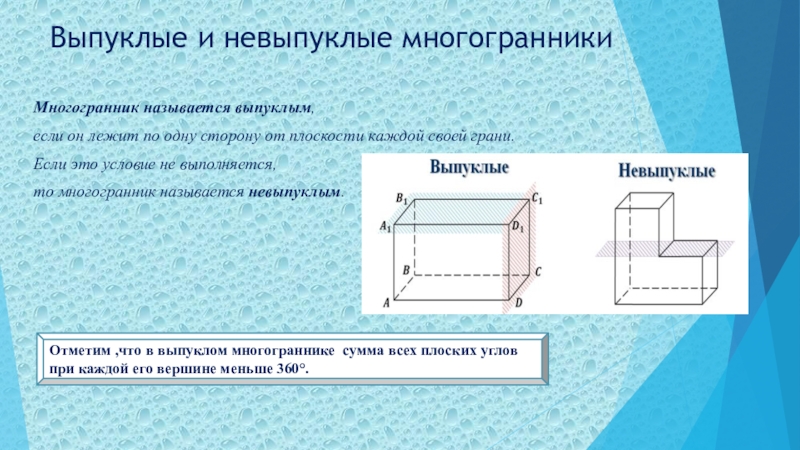
Многогранник называется выпуклым,
если он лежит по
одну сторону от плоскости каждой своей грани.
Если это условие не
выполняется,
то многогранник называется невыпуклым.
Отметим ,что в выпуклом многограннике сумма всех плоских углов при каждой его вершине меньше 360°.
Слайд 5Теорема Эйлера
В любом выпуклом многограннике сумма числа граней и числа
вершин больше числа ребер на 2.
Для
любого выпуклого многогранника справедливо соотношение :
Г+В-Р=2 ,
где
Г – число граней
В – число вершин
Р – число ребер данного многогранника
Слайд 6Призма.
Это многогранник , две грани которого являются равными многоугольниками , лежащими
в параллельных плоскостях, а остальные грани — параллелограммами , имеющими общие
стороны с этими многоугольниками.
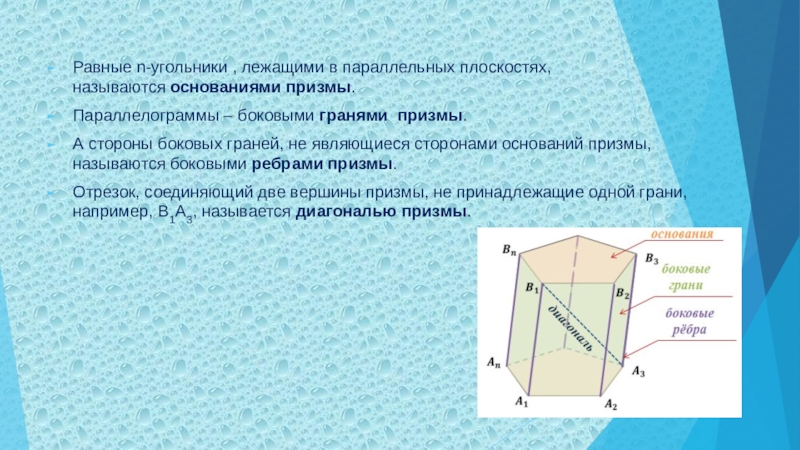
Слайд 7Равные n-угольники , лежащими в параллельных плоскостях, называются основаниями призмы.
Параллелограммы
– боковыми гранями призмы.
А стороны боковых граней, не являющиеся сторонами
оснований призмы, называются боковыми ребрами призмы.
Отрезок, соединяющий две вершины призмы, не принадлежащие одной грани, например, B1A3, называется диагональю призмы.
Слайд 8Призма в зависимости от того какой многоугольник лежит в основании
имеет свое название.
Если в основании лежит треугольник, то призма
называется треугольной.
Если четырехугольник – то четырехугольной призмой.
А если n-угольник, то n-угольной призмой.
Слайд 9Высота призмы
Выберем произвольную точку А одного из оснований и проведем
через нее прямую, перпендикулярную к плоскости другого основания и пересекающую
ее в точке B.
Отрезок, AB называется высотой призмы.
Слайд 10∙Если все боковые ребра призмы перпендикулярны к плоскостям ее оснований,
то призма называется прямой.
∙Если же боковые ребра не перпендикулярны основанию,
то призма называется наклонной.
Прямая призма, основаниями которой являются правильные многоугольники, называется правильной.
Слайд 11Пирамида
∙Многогранник, составленный из n-угольника A1A2…An и этих n треугольников, называется пирамидой.
∙Многоугольник A1A2…An называется основанием
пирамиды.
∙Треугольники PA1A2, PA2A3, …, PAnA1 называются
боковыми гранями пирамиды.
∙Точка P – вершиной пирамиды,
а отрезки PA1, PA2,…, PAn – ее боковыми ребрами.
∙Отрезок, соединяющий вершину пирамиды
с плоскостью ее основания и перпендикулярный к этой плоскости, называется высотой пирамиды.
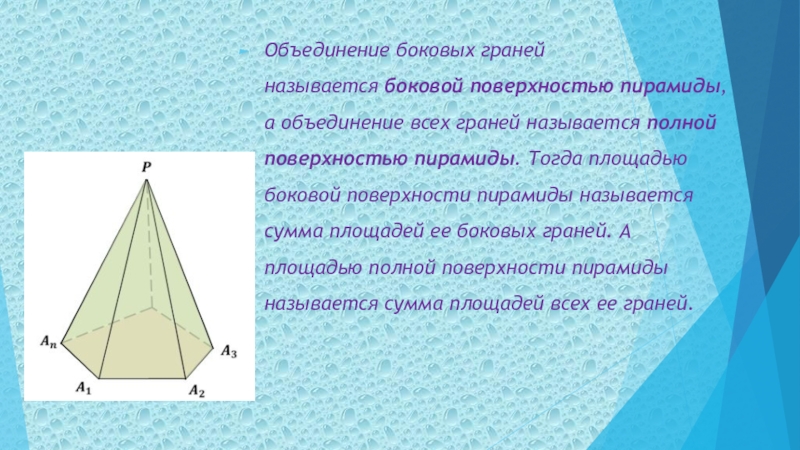
Слайд 12Объединение боковых граней называется боковой поверхностью пирамиды, а объединение всех граней
называется полной поверхностью пирамиды. Тогда площадью боковой поверхности пирамиды называется сумма
площадей ее боковых граней. А площадью полной поверхности пирамиды называется сумма площадей всех ее граней.
Слайд 13Пирамида в зависимости от того какой многоугольник лежит в основании
имеет свое название. Если в основании лежит треугольник, то пирамида
называется треугольной. Если четырехугольник – то четырехугольной пирамидой. А если n-угольник, то n-угольной пирамидой.
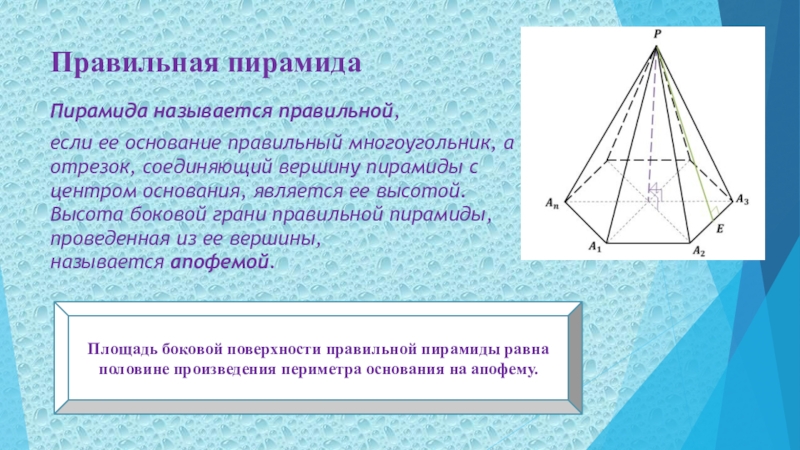
Слайд 14Правильная пирамида
Пирамида называется правильной,
если ее основание правильный многоугольник, а
отрезок, соединяющий вершину пирамиды с центром основания, является ее высотой.
Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой.
Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.
Слайд 15Усеченная пирамида
Плоскость β разбивает пирамиду на две фигуры.
A1A2B2B1, A2A3B3B2,…, AnA1B1Bn называется усеченной
пирамидой.