Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Школы математики Древней Греции 5-6 класс
Содержание
- 1. Школы математики Древней Греции 5-6 класс
- 2. ПЭФДЕАПАГ
- 3. ПИФАГОРПИФАГОР – древнегреческий математик , основатель пифагорейской
- 4. ПИФАГОРЕЙСКАЯ ШКОЛАРафаэль Санти. Пифагор (деталь Афинской школы)ОПифагор
- 5. Пифогоровы тройки
- 6. АРХИМЕДАрхимед родился в 287 году до
- 7. ЛЕГЕНДЫ ОБ АРХИМЕДЕ. В наше время имя
- 8. Задача о коронеКорона весит 60 мин (греческая
- 9. ЕВКЛИДЕвклид (ок. 365 – ок.300 до н.э.).
- 10. Задачи на разрезаниеПопробуйте разрезать изображенную на рисунке
- 11. АППОЛОНИЙАпполоний Пергский (ок.260 – 170 до н.э.)
- 12. ТанграмТанграм - очень древняя игра – головоломка.
- 13. ФАЛЕС Фалес из Милета (ок.625
- 14. Задачи со спичками1.Переложите 4 спички так, чтобы
- 15. ЭРАТОСФЕН Эратосфен Киренский (ок. 276
- 16. Фигурные числа
- 17. ГЕРОНГерон Александрийский великий физик, математик, механик и
- 18. Задача Герона Александрийского. Из под земли
- 19. ПЛАТОН
- 20. «Суд Париса» Богини Гера, Афродита и Афина
- 21. ДИОФАНТ В конце II в. н.э. начинается закат
- 22. ЗАДАЧА МЕТРОДОРАНа памятнике древнегреческому математику Диофанту есть
- 23. Скачать презентанцию
ПЭФДЕАПАГ
Слайды и текст этой презентации
Слайд 3ПИФАГОР
ПИФАГОР – древнегреческий математик , основатель пифагорейской школы.
Родился в 570
году до н. э. на острове Самос в Эгейском море.
Слайд 4ПИФАГОРЕЙСКАЯ ШКОЛА
Рафаэль Санти.
Пифагор (деталь Афинской школы)
О
Пифагор в молодости для
изучения наук жрецов путешествовал по Египту, жил также в Вавилоне,
где имел возможность в течение 12 лет изучать астрологию и астрономию у халдейских жрецов. После Вавилона переселился в Южную Италию, а потом в Сицилию, где организовал пифагорейскую школу, которая внесла ценный вклад в развитие математики и астрономии.Теорема Пифагора входит во все курсы элементарной геометрии как одна из основных теорем.. Доказанная Пифагором знаменитая теорема носит его имя. Трудно найти человека, у которого имя Пифагора не ассоциировалось бы с теоремой Пифагора. Даже те, кто в своей жизни далек от математики, продолжают сохранять воспоминания о «пифагоровых штанах» - квадрате на гипотенузе, равновеликом двум квадратам на катетах
Слайд 6
АРХИМЕД
Архимед родился в 287 году до нашей эры в греческом
городе Сиракузы, где и прожил почти всю свою жизнь. Учился
Архимед в Александрии, где правители Египта Птолемеи собрали лучших греческих ученых и мыслителей, а также основали самую большую в мире библиотеку. Основные работы Архимеда касались различных практических приложений математики , физики, гидростатики и механики. В сочинении "Параболы квадратуры" Архимед обосновал метод расчета площади параболического сегмента, причем сделал это за две тысячи лет до открытия интегрального исчисления. В труде "Об измерении круга" Архимед впервые вычислил число "пи" - отношение длины окружности к диаметру - и доказал, что оно одинаково для любого круга.
Слайд 7ЛЕГЕНДЫ ОБ АРХИМЕДЕ.
В наше время имя Архимеда связывают главным
образом с его замечательными математическими работами, однако в античности он
прославился также как изобретатель различного рода механических устройств и инструментов, о чем сообщают авторы, жившие в более позднюю эпоху. Считается, что Архимед был изобретателем т.н. архимедова винта, который служил для подъема воды на поля и явился прообразом корабельных и воздушных винтов.Вызывает сомнение и подлинность истории, поведанной Витрувием, что будто бы царь поручил Архимеду проверить, из чистого ли золота сделана его корона или же ювелир присвоил часть золота, сплавив его с серебром. «Размышляя над этой задачей, Архимед как-то зашел в баню и там, погрузившись в ванну, заметил, что количество воды, переливающейся через край, равно количеству воды, вытесненной его телом. Это наблюдение подсказало Архимеду решение задачи о короне, и он, не медля ни секунды, выскочил из ванны и, как был нагой, бросился домой, крича во весь голос о своем открытии: «Эврика! Эврика!» (греч. «Нашел! Нашел!»)».
При обороне Сиракуз от осаждавших этот город римских войск Архимед создал подъемные и метательные машины, а «зажигательное зеркало», с помощью которого он якобы сжег корабли доныне остается загадкой, волнующей умы исследователей.
Слайд 8Задача о короне
Корона весит 60 мин (греческая мера) и состоит
из сплава золота, меди, олова и железа.
Золото и медь составляют
вместе 2/3, золото и олово- ¾, золото и железо -3/5 общего веса.Определить вес каждого металла в отдельности.
Слайд 9ЕВКЛИД
Евклид (ок. 365 – ок.300 до н.э.). История почти не
сохранила сведений о жизни и деятельности ученого. Известно лишь, что
он написал ряд книг по математике, физике, астрономии. До нас дошли всемирно известные «Начала». В тринадцати книгах «начал» Евклид подвел итог за 350-летний период в развитии античной математики и заложил логический фундамент ее дальнейшего прогресса. Книга «Начала» стали высшим образцом построения научных теорий. В знаменитом сочинении Евклида были систематизированы основные известные в то время геометрические сведения, был развит аксиоматический подход к построению геометрии.Слайд 10Задачи на разрезание
Попробуйте разрезать изображенную на рисунке фигуру на 3
равные по форме части:
Разрежьте теперь эту фигуру на 4 равные
по форме части:Слайд 11АППОЛОНИЙ
Апполоний Пергский (ок.260 – 170 до н.э.) – наряду с
Архимедом и Евклидом третий из самых выдающихся ученых эпохи эллинизма.
Автор нескольких работ по математике и астрономии, среди которых наиболее известны восемь книг трактата «Конические сечения» (восьмая книга не дошла до нас).«Конические сечения» - яркий пример теории, возникшей из логики развития самой математики и лишь со временем нашедшей практическое применение. Теория конических сечений Апполония нашла применение лишь в XVI – XVII вв., когда Кеплер установил, что планеты Солнечной системы движутся по эллипсам, а Галилей показал, что брошенный камень (снаряд) летит в пустоте по параболе.
Слайд 12Танграм
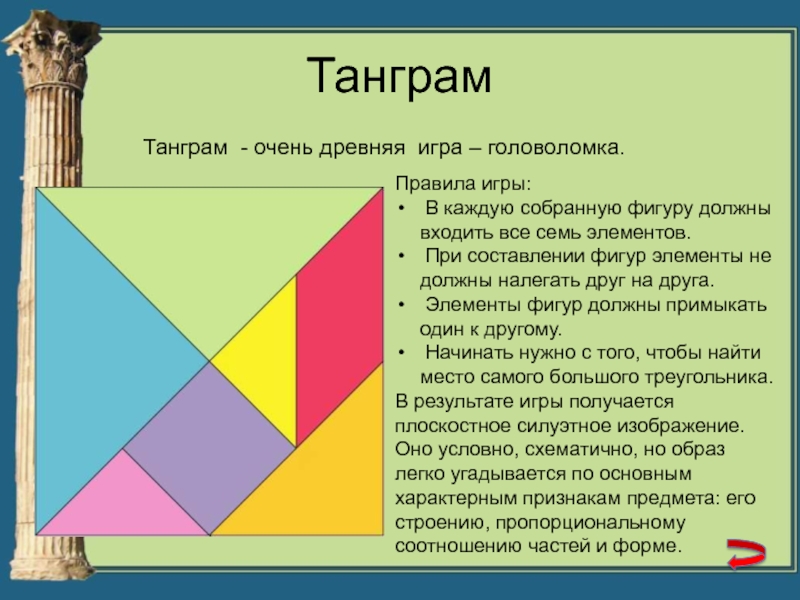
Танграм - очень древняя игра – головоломка.
Правила игры:
В каждую собранную фигуру должны входить все семь элементов.
При
составлении фигур элементы не должны налегать друг на друга.Элементы фигур должны примыкать один к другому.
Начинать нужно с того, чтобы найти место самого большого треугольника.
В результате игры получается плоскостное силуэтное изображение. Оно условно, схематично, но образ легко угадывается по основным характерным признакам предмета: его строению, пропорциональному соотношению частей и форме.
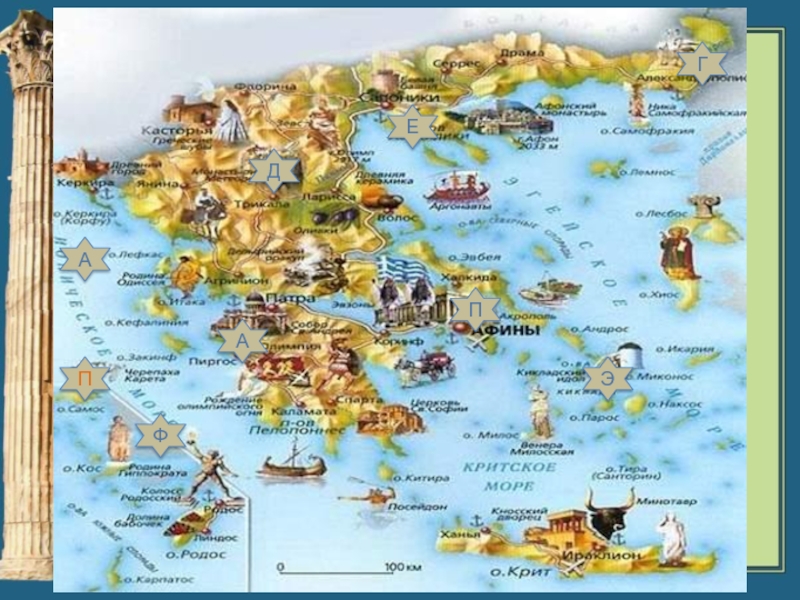
Слайд 13ФАЛЕС
Фалес из Милета (ок.625 – ок.547 до
н.э.) древнегреческий ученый и государственный деятель, первый из семи мудрецов.
Зачинатель и родоначальник греческой философии и науки. Ему приписывают открытия
диаметр делит круг пополам;
углы при основании равнобедренного треугольника равны;
вертикальные углы равны;
треугольники равны, если они обладают равной стороной и двумя прилежащими к ней углами.
Фалес определял высоту предмета по его тени, расстояния до кораблей, используя подобие треугольников.
Он сделал ряд открытий в области астрономии, установил время равноденствий и солнцестояний, Определил продолжительность года. Фалес был причислен к группе «семи мудрецов».
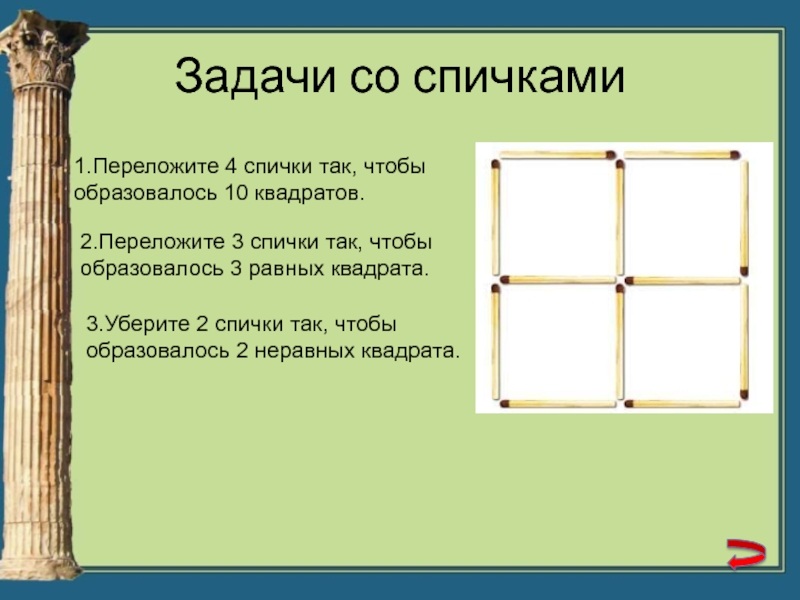
Слайд 14Задачи со спичками
1.Переложите 4 спички так, чтобы образовалось 10 квадратов.
2.Переложите
3 спички так, чтобы образовалось 3 равных квадрата.
3.Уберите 2 спички
так, чтобы образовалось 2 неравных квадрата.Слайд 15ЭРАТОСФЕН
Эратосфен Киренский (ок. 276 – 194 до
н.э.) – разносторонний ученый: математик, астроном, географ, историк и филолог.
Прославился благодаря изобретению «решета Эратосфена». В сочинении « Решето» Эратосфен создал оригинальный метод для «отсеивания» простых чисел. В последовательности натуральных чисел зачеркнем 1. Число 2-простое. Зачеркнём все числа, кратные 2. Число 3- первое из незачеркнутых – простое. Затем зачеркнем всякое число, делящееся на 3, и т. д. Так можно получить сколь угодно большой фрагмент последовательности простых чисел. Во времена Эратосфена писали на восковых дощечках. Числа не зачёркивали, а прокалывали. Отсюда и название метода- решето. Осуществил первое измерение размеров земли. Измерив длину 1/50 дуги земного меридиана, Эратосфен вычислил окружность земного шара и получил 25 200 стадий, или 39 960 км, что лишь на 319 км меньше действительного значения.Слайд 17ГЕРОН
Герон Александрийский великий физик, математик, механик и инженер древней Греции
Герона
относят к величайшим инженерам за всю историю человечества. Он первым
изобрёл автоматические двери, автоматический театр кукол, автомат для продаж, скорострельный самозаряжающийся арбалет, паровую турбину, автоматические декорации, прибор для измерения протяженности дорог (древний «таксометр») и др. Первым начал создавать программируемые устройства. Много работ Герона Александрийского было посвящено Математике. Больше всего в его работах формул по геометрии, задач по вычислению геометрических фигур. Так же здесь описывается и знаменитая формула Герона, с помощью которой можно вычислить площадь треугольника по трем сторонам.Слайд 18Задача
Герона Александрийского.
Из под земли бьют четыре источника.
Первый заполняет
бассейн за один день,- второй- за два дня, третий- за
три дня, четвертый- за четыре дня.За сколько времени наполнят бассейн все четыре источника вместе?
Слайд 19ПЛАТОН
Девиз академии Платона
был:
"Не знающие геометрии не допускаются!"
Уже к началу IV века до
н. э. греческая математика далеко опередила всех своих учителей, и её бурное развитие продолжалось. В 389 году до н. э. Платон основывает в Афинах свою школу - знаменитую Академию. Математиков, присоединившихся к Академии, можно разделить на две группы: на тех, кто получил своё математическое образование вне Академии, и на учеников Академии. К числу первых принадлежали Теэтет Афинский, Архит Тарентский и позднее Евдокс Книдский; к числу вторых - Амикл из Гераклеи, братья Менехм и Динострат.Сам Платон конкретных математических исследований не вёл, но опубликовал глубокие рассуждения по философии и методологии математики. А ученик Платона, Аристотель, оставил бесценные для нас записки по истории математики.
Слайд 20«Суд Париса»
Богини Гера, Афродита и Афина пришли к юному Парису,
чтобы тот решил, кто из них прекраснее. Представ перед Парисом,
богини высказали следующие утверждения.Афродита. Я самая прекрасная. (1)
Афина. Афродита не самая прекрасная. (2)
Гера. Я самая прекрасная. (3)
Афродита. Гера не самая прекрасная. (4)
Афина. Я самая прекрасная. (5)
Парис, прилёгший отдохнуть на обочине дороги, не счёл нужным даже снять платок, которым прикрыл глаза от яркого солнца. Но богини были настойчивы, и ему нужно было решить, кто из них самая прекрасная. Парис предположил, что все отверждения прекраснейшей из богинь истинны, а все утверждения двух остальных богинь ложны. Мог ли Парис вынести решение, кто прекраснее из богинь?
Слайд 21ДИОФАНТ
В конце II в. н.э. начинается закат греческой математики.
На
фоне общего застоя и упадка резко выделяется гигантская фигура Диофанта
- последнего из великих античных математиков, «отца алгебры».Главный труд Диофанта- «Арифметика», по предположению, состоит из 13 книг .
Заслуги Диофанта:
1. Отказ от геометрической алгебры древних греков. Введение буквенной алгебры (в зачатом состоянии), алгебраической символики.
2. Расширение понятия числа.
3. Заложил основы теории неопределённых уравнений, которые приводят в последствии к теории чисел.
4.Если древнегреческая геометрическая алгебра имела дело со степенями не выше третьей, то Диофант это ограничение фактически снимает.
5.Диофант расширяя понятия числа. наряду с положительными числами вводит отрицательные числа и отрицательные показатели степеней., а также умножения степеней.
Слайд 22ЗАДАЧА МЕТРОДОРА
На памятнике древнегреческому математику Диофанту есть следующая запись, известная
под названием задача Метродора.
Здесь погребен Диофант, и камень могильный
При
счете искусном расскажет нам, Сколь долог был его век.
Велением бога он мальчиком был шестую часть своей жизни;
В двенадцатой части затем прошла его светлая юность.
Седьмую часть жизни прибавим- перед нами очаг Гименея.
Пять лет протекли, и прислал Гименей ему сына.
Но горе ребенку! Едва половину он прожил
Тех лет, что отец, как скончался несчастный.
Четыре года страдал Диофант от утраты такой тяжелой
И умер, прожив для науки. Скажи мне,
Скольких лет достигнув, смерть воспринял Диофант?