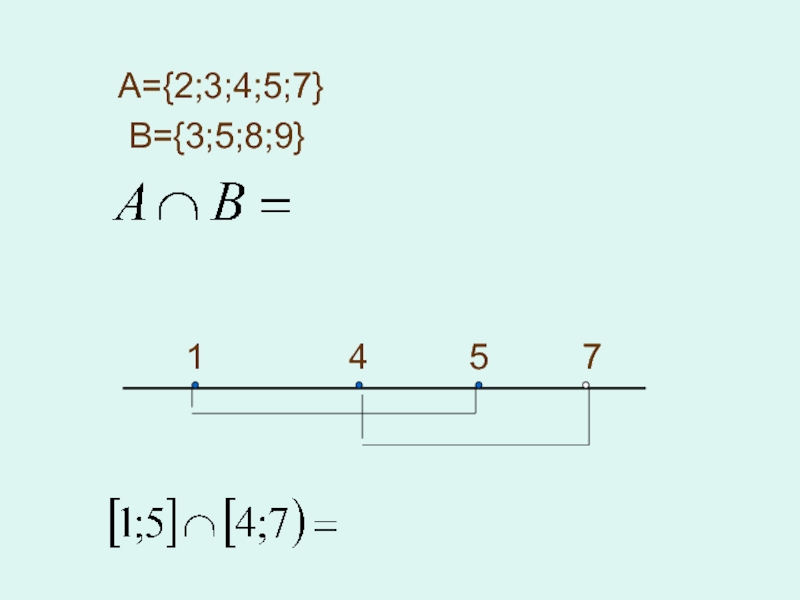Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Множества
Содержание
- 1. Множества
- 2. Множество есть многое, мыслимое нами как единое Георг Кантор
- 3. Способы задания множеств:1.Описание.Описание, включает основной, характеристический признак
- 4. АОбозначения множеств{2, 3, 4, 5, 6, 7}круги Эйлерасb25[2;5]-37[-3;7)
- 5. ПримерыМножество синицМножество воробьев
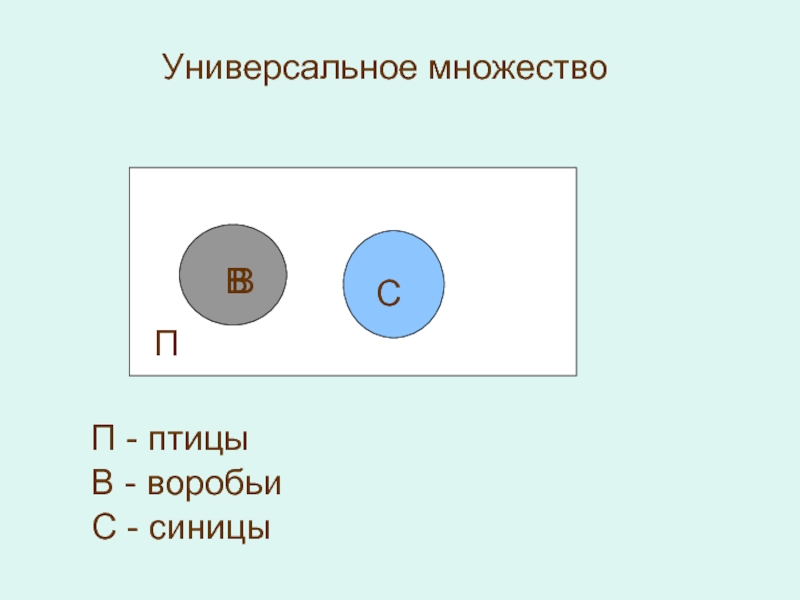
- 6. Универсальное множествоПВВСП - птицыВ - воробьиС - синицы
- 7. Обозначение универсального множестваIАА – подмножество IА включается в I
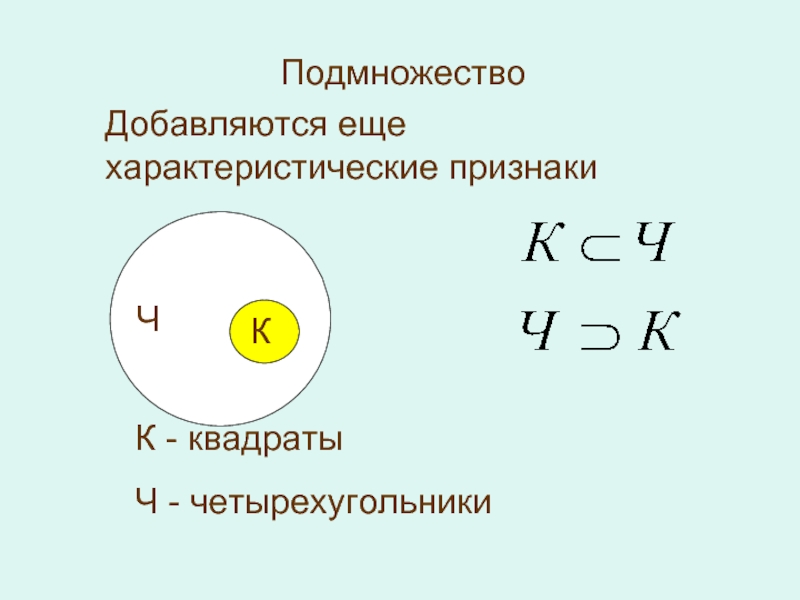
- 8. ПодмножествоКЧК - квадратыЧ - четырехугольникиДобавляются еще характеристические признаки
- 9. Пустое множествоМножество называется пустым, если в нем нет ни одного элемента
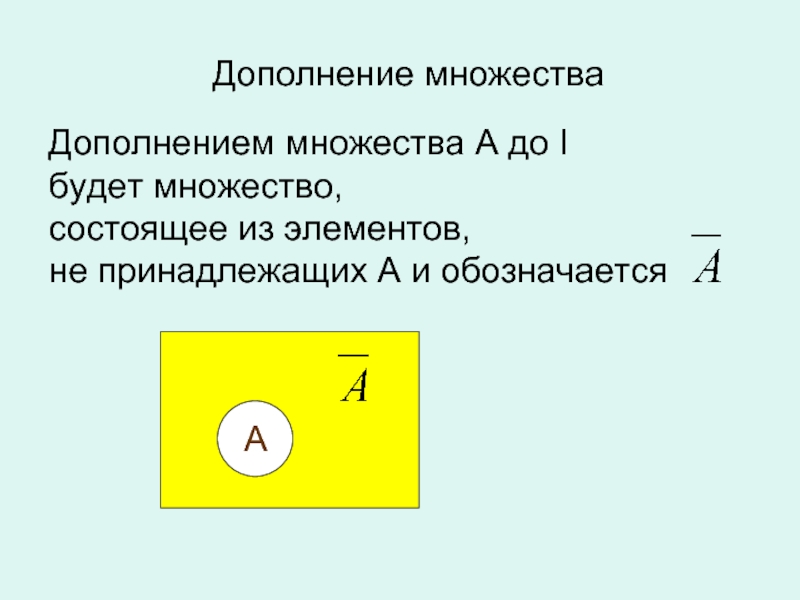
- 10. Дополнение множестваДополнением множества А до I будет
- 11. Урок 5Действия с множествами
- 12. Действия с множествами1.Объединением множеств А и В называется множество, состоящее из элементов, принадлежащих А или В.АВxyzr
- 13. А={2;3;4;5;7}B={3;5;8;9}1457
- 14. 2. Пересечением множеств А и В называется множество, состоящее из элементов, принадлежащих А и В. ABxyrz
- 15. А={2;3;4;5;7}B={3;5;8;9}1457
- 16. Слайд 16
- 17. , , ,Разностью множеств А и
- 18. Cр-1Ф.И.
- 19. Скачать презентанцию
Множество есть многое, мыслимое нами как единое Георг Кантор
Слайды и текст этой презентации
Слайд 3Способы задания множеств:
1.Описание.
Описание, включает основной,
характеристический признак множества
2.Список
Например, множество
учеников нашего класса
![АОбозначения множеств{2, 3, 4, 5, 6, 7}круги Эйлерасb25[2;5]-37[-3;7)](/img/tmb/1/30138/11c5976448f404abe2523a1e6f62b18b-800x.jpg "Множества АОбозначения множеств{2, 3, 4, 5, 6, 7}круги Эйлерасb25[2;5]-37[-3;7)")
Слайд 10
Дополнение множества
Дополнением множества А до I
будет множество,
состоящее из
элементов,
не принадлежащих А и обозначается
А
Слайд 12Действия с множествами
1.Объединением множеств А и В
называется множество,
состоящее
из элементов, принадлежащих
А или В.
А
В
x
y
z
r
Слайд 142. Пересечением множеств А и В
называется множество,
состоящее из
элементов,
принадлежащих А и В.
A
B
x
y
r
z
Слайд 17
,
,
,
Разностью множеств А и В называется
множество,
состоящее из элементов,
принадлежащих А, но не принадлежащих В
если
С= А\В
и
Неоднозначная
операция если
если
Теги
