Н?ктелерді? геометриялы? орны ?дісі

әдісі

Мысал

шеңбері мен
түзуі берілген. Шеңберден тыс орналасып, берілген

мен шеңберден

қашықтықта орналасқан нүкте салу керек.

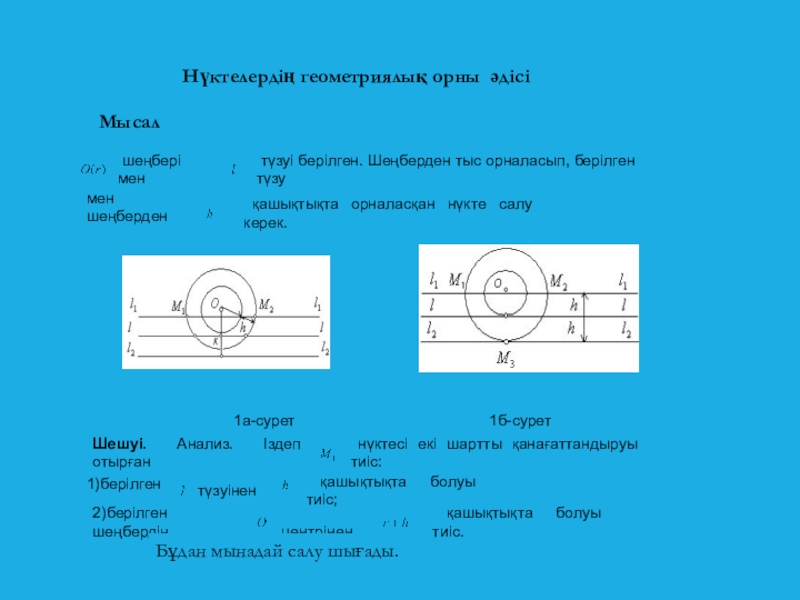
1а-сурет 1б-сурет

Шешуі. Анализ. Іздеп отырған

нүктесі екі шартты қанағаттандыруы тиіс:

1)берілген

түзуінен

қашықтықта болуы тиіс;

2)берілген шеңбердің

центрінен

қашықтықта болуы тиіс.

Бұдан мынадай салу шығады.

орны – параллель қос түзу саламыз.
2)
шеңберін саламыз.
3) Салынған нүктелердің

және

деп белгілейміз.

мен

-

іздеп отырған нүктелеріміз

Дәлелдеме.

және

нүктелері екі нүктелердің геометриялық орнының

қилысу нүктелері

есебінде

екі шартты да қанағаттандырады. Олай болса, бұл нүктелер іздеп

отырған нүктелеріміз.

Зерттеу. 1 – 2 салулар барлық уақытта орындалады және бір мәнді болады. Шешімдерінің болуы – берілген

түзуі

мен

шеңберінің өз ара

орналасуына байланысты.

Әр түрлі жағдайларды қарастырайық.

1)Берілген

түзуі берілген

шеңберін қиып өтпейді (1 а-сурет).

Бұл жағыдай да, егер

центрінен

түзуіне дейінгі

қашықтығы

шартын қанағаттандыратын болса, онда есептің екі тек қана екі шешімі

болады. Шындығында, егер есептің екіден артық шешімі болады десек, онда

түзу шеңберді екі нүктеде ғана емес

одан да көп нүктеде қиып өтеді, бұлай болуы мүмкін емес.

Егер

болса, онда есептің бір ғана шешімі болады.

шеңберін жанап өтеді (1,б-сурет). Бұл жағдай да
-тың
кез келген

мәнінде есептің үш шешімі болады.

3)

түзуі мен

шеңбері қилысады (1, в-сурет). Бұл жағдайда есептің барлық

уақытта төрт шешімі болады.

1в-сурет

Симметрия әдісі
Мысал
мен

қабырғалары және

мен

бұрыштарының

айырмасы бойынша

үщбұрыш салу керек.

3-сурет

Шешуі. Анализ.

үшбұрышы салынған делік (3-сурет). Олай

болса,

жә не

нүктелерінің

симметралін салып,

кесіндісін

түзуімен

салыстырып бейнелейік.

болып шығады.

Сонда шыққан бұрыштарды қарастырсақ,

яғни

қорытындыға келеміз.

болады деген

Сонымен, есеп екі қабырғасы және сол қабырғалар арасындағы бұрыштары бойынша көмекші

үшбұрышын салуға келіп тіреледі.

Салу. 1)

үшбұрышын саламыз (

бойынша).

2)

және

нүктелерінің симметриялы -

түзуін жүргіземіз.

- іздеп отырған үшбұрышымыз.
Дәлелдеме. Салу бойынша
үшбұрышында
Симметрияның қасиеті

Бұдан

үшбұрышында қабырғалар

екендігі шығады.

үшбұрышы

үшбұрышына тең.

Зерттеу. Егер

(үшбұрышта үлкен бұрышқа қарысы үлкен қабырға жатады) және

болса, онда есептің бір ғана шешімі болады (тең екі үшбұрыш).

Егер

болса, онда есептің шешімі болмайды.

Егер

болса, бұл жағдайда да есептің шешімі болмайды.

Өйткені үшбұрыштың екі бұрышының айырмасы

тан кіші болуы тиіс.

Параллель көшіру әдісі
Мысал
төрт қабырғасы бойынша трапеция салу керек.
1-сурет
Шешуі.

- іздеп отырған трапециямыз болсын (1-сурет).

қабырғасын

қалпына келтіріп,

векторына көшіреміз, сонда

нүктесі

нүктесіне ығысады.

Сонда үш қабырғасы бойынша

үшбұрышын салуға болады:

және

Сонан соң

-ді

бұрынғы қалпына

векторына көшірсек, іздеп отырған трапециямыз шығады.

Слау.

қабырғалары бойынша

үшбұрышын саламыз.

қабырғасын

параллель етіп

векторына көшіріп

орынға келтірейік (

векторының модулі

ға тең).

- іздеп отырған трапециямыз (1-суретті қараңыз).

көшірудің қасиеті бойынша

Сонымен,
трапециясында:

болады.
Зерттеу. Зерттеу
үшбұрышын үш қабырғасы бойынша

мүмкін болғандықтан шарттарын анықтауға

келіп тіреледі

Зерттеу мына төмендегіден тұрады:

салу керек.
Шешуі. Анализ.
үшбұрышы салынған делік (1-сурет).

қабырғасының ортасы.

нүктесін

нүктесінің айналасында

-қа тең бұрышқа айналдыру (сағат стрелкасы бағытымен) арқылы

нүктесіне көшіруге болатындығын байқаймыз.

үшбұрышын

нүктесін айналдыра

-қа бұрсақ

көмекші

және

үшбұрыштарын

аламыз, соңғы

үшбұрышын үш қабырғасы

(

және

) арқылы салуға болады.

1-сурет

Бұдан іздеп отырған үшбұрышымызды салу тәсілі келіп шығады.

Салу.

үш қабырғасы бойынша

үшбұрышын, сонан соң

қабырғасының ортасы -

нүктесін саламыз.

үшбұрышын

центрінен

-қа тең бұрышқа айналдырайық

(сағат

cтрелкасының бағытына қарсы). Сонада

нүктесі

нүктесінің орнына келеді.

- іздеп отырған

үшбұрышымыз.

Дәлеледеме. Салу бойынша

үшбұрышында

қабырғадары
және
болады.
үшбұрышын салуға болатын болса, онда

болғанда,

үшбұрышын салуға болады.

Зерттеу. Егер көмекші

да салуға болады. Ал