Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
О множествах 9 класс
Содержание
- 1. О множествах 9 класс
- 2. ЧТО ТАКОЕ МНОЖЕСТВО? (1)Множества могут состоять из
- 3. ЧТО ТАКОЕ МНОЖЕСТВО? (2)«Множество есть многое, мыслимое
- 4. Виды множествОсновные виды множеств, с которыми мы
- 5. Как задают множества ?Перечислением всех элементов(для конечных
- 6. П у с т о е
- 7. Это интересно!!Не решена проблема Ферма: Пусто ли
- 8. ПодмножествоПусть даны два множества А и В.
- 9. N Z Q R
- 10. Операции над множествамиПересечение множеств Пересечением множеств А,
- 11. Операции над множествамиА В Объединение или сумма
- 12. Операции над множествамиЕсли множество Х является суммой
- 13. Операции над множествами Разностью множеств А и
- 14. В случае, когда множество В является частью
- 15. Как сравнивать множестваВ каком случае надо говорить,
- 16. Равна ли часть целому?Основная догма, которую необходимо
- 17. Трудно примериться, что дорога в миллион световых
- 18. Тайны бесконечностиМатематики и философы всегда интересовались понятием
- 19. Основные заслуги в развитии теории множеств
- 20. Используемая литература1. Виленкин Н.Я. «Рассказы о множествах»/
- 21. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2ЧТО ТАКОЕ МНОЖЕСТВО? (1)
Множества могут состоять из различных элементов –
рыб, домов, квадратов, чисел, точек и т.д.
чрезвычайная широта теории множеств и её приложимость к самым разным областям знаний(математике, механике, физике, биологии, лингвистике м т.д.Слайд 3ЧТО ТАКОЕ МНОЖЕСТВО? (2)
«Множество есть многое, мыслимое нами как единственное».
Георг
Кантор (основатель теории множеств)
Нет строгого определения. Это основное понятие. В
обиходном языке – это «совокупность», «собрание», «коллекция», «класс», «система» и тд.Это несколько объектов объединённых общим признаком
(множество стульев в комнате, множество атомов на Юпитере, множество картофелин в данном мешке, множество рыб в океане, множество точек на окружности и тд).
Предметы составляющие данное множество – его элементы:
А = {х, у,…,z}, x A.
C –множество дней недели, то С={понедельник, вторник, среда, четверг, пятница, суббота, воскресенье}; январь С, среда С
Слайд 4Виды множеств
Основные виды множеств, с которыми мы познакомимся:
Конечные
Пустое
Бесконечные(счётные,
несчётные)
Счётное множество – самое маленькое из бесконечных*
Несчётные множества существуют.
Например: множество всех точек на прямой линии. Доказать несчётность нелегкоСлайд 5Как задают множества ?
Перечислением всех элементов(для конечных множеств)
Указанием характеристического свойства
(оно
должно формулироваться тщательно, чтобы избежать неясности и двусмысленности, свойственных обычному
нашему языку)Слайд 6П у с т о е м н о
ж е с т в о. Зачем они нужны?
Множество не
содержащее ни одного элемента называют пустым и обозначают ØНапример
- Множество лошадей, пасущихся на луне,
- множество десятиногих млекопитающих,
- множество действительных решений
уравнения х2 = - 4
Когда множество задано характеристическим свойством, то не всегда известно, существует ли хоть один элемент с таким свойством.
Пустое множество единственное: нет двух разных пустых множеств.
Слайд 7Это интересно!!
Не решена проблема Ферма:
Пусто ли множество натуральных чисел
n таких, что n > 2, уравнение хn + уn
=zn имеет положительные целочисленные решения.Слайд 8Подмножество
Пусть даны два множества А и В. причём каждый элемент
второго множества является элементом первого множества. Тогда В называют подмножеством
(или частью) множества А. Записывают это так: А В(Читают: «множество В содержится в множестве А» или «множество А содержит множество В»).
Считается, что пустое множество Ø является подмножеством любого множества.
В
А
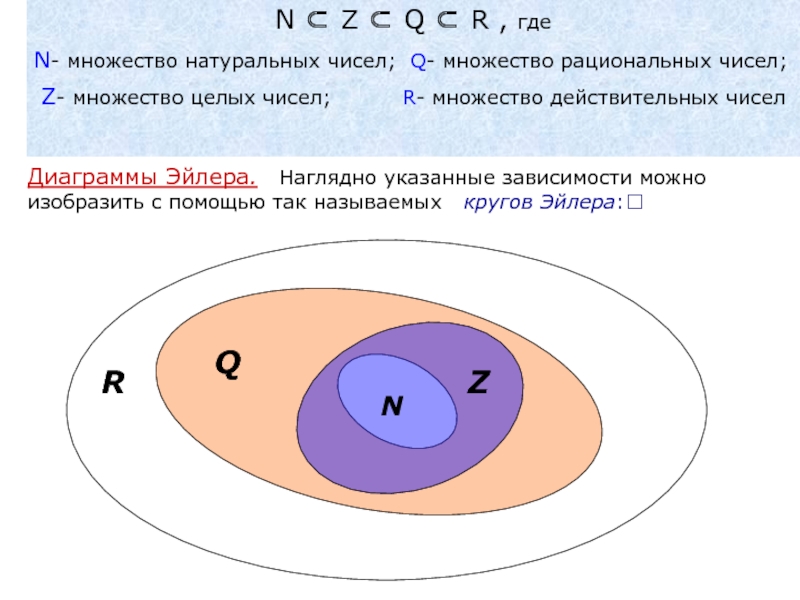
Слайд 9N Z Q R , где
N-
множество натуральных чисел; Q- множество рациональных чисел;
Z- множество
целых чисел; R- множество действительных чиселZ
N
R
Q
Диаграммы Эйлера. Наглядно указанные зависимости можно изобразить с помощью так называемых кругов Эйлера:
Слайд 10Операции над множествами
Пересечение множеств
Пересечением множеств А, В, С,… называется
множество, состоящее из всех элементов, принадлежащих каждому из этих множеств.
закрашенная фигура А В - пересечение___________________________
Пересечение множеств иногда называют их произведением, а операцию пересечения – умножением множеств. Многие свойства пересечения напоминают свойства умножения чисел.
Слайд 11Операции над множествами
А В
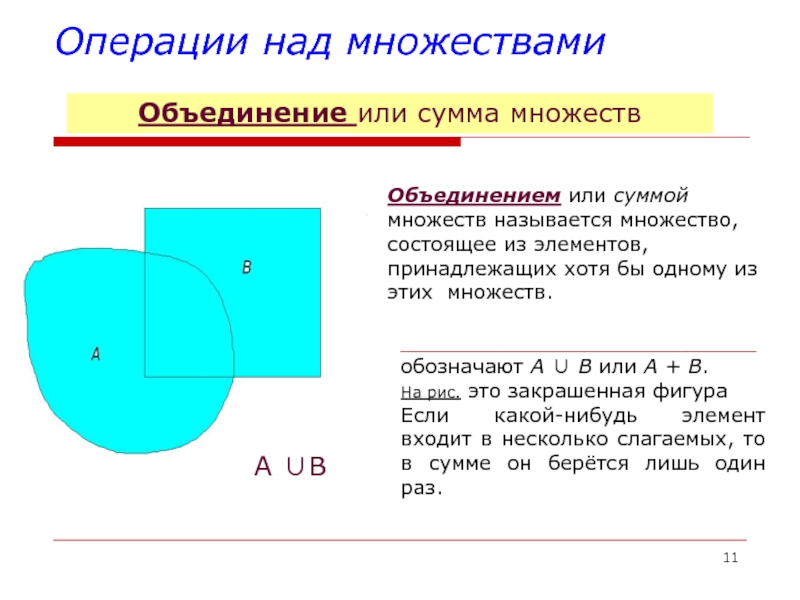
Объединение или сумма множеств
Объединением или
суммой множеств называется множество, состоящее из элементов, принадлежащих хотя бы
одному из этих множеств.____________________________
обозначают А В или А + В.
На рис. это закрашенная фигура
Если какой-нибудь элемент входит в несколько слагаемых, то в сумме он берётся лишь один раз.
Слайд 12Операции над множествами
Если множество Х является суммой множеств А, В
,С,…, причём никакие два из них не имеют общих элементов,
то говорят, что множество Х разбито на (непересекающиеся) подмножества А, В ,С,… .Примеры
а) Множество натуральных чисел разбивается на подмножества чётных и нечётных чисел.
б) Множество учеников в классе на подмножества учеников, фамилии которых начинаются на одну и ту же букву.
Разбиение множества на попарно непересекающиеся подмножества называют классификацией, а полученные подмножества – классами.
Разбиение множеств.
Слайд 13Операции над множествами
Разностью множеств А и В называют такое
множество Х = А\ В или (А – В), в
которое входят все элементы из А, не принадлежащие множеству В.При этом не предполагается, что множество В является частью множества А.
Таким образом при вычитании множества В из А из А удаляют общую часть (пересечение) А и В:
А\ В = А \ А В.
Например.
А – множество всех учащихся IX класса данной школы, а В – множество всех девочек России,
то Х= А\ В – множество всех мальчиков, обучающихся в IX классе этой школы.
Вычитание множеств
Слайд 14В случае, когда множество В является частью А , разность
множеств А – В называют дополнением.
Дополнением множества В до
множества А называется множество всех элементов А, не являющихся элементами множества В. На рисунке это закрашенная фигура
Операции над множествами
Дополнение множеств
Слайд 15Как сравнивать множества
В каком случае надо говорить, что одно множество
содержит столько элементов, сколько и второе?
В каких случаях два
бесконечных множества имеют «поровну» элементов? Слайд 16Равна ли часть целому?
Основная догма, которую необходимо отбросить: «часть меньше
целого»
На длинном и коротком отрезках точек поровну
Как сравнивать множества
О
В
С
D
А
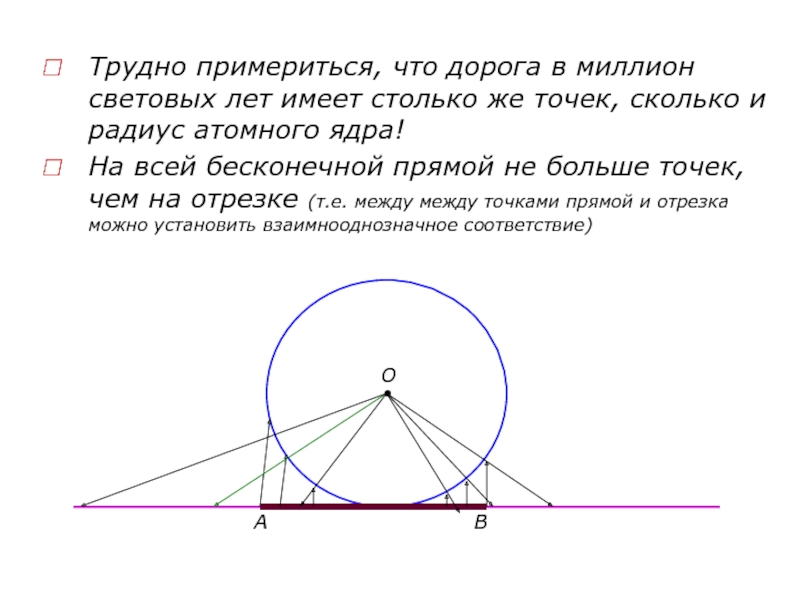
Слайд 17Трудно примериться, что дорога в миллион световых лет имеет столько
же точек, сколько и радиус атомного ядра!
На всей бесконечной прямой
не больше точек, чем на отрезке (т.е. между между точками прямой и отрезка можно установить взаимнооднозначное соответствие)О
А
В
Слайд 18Тайны бесконечности
Математики и философы всегда интересовались понятием бесконечности.
Парадоксы бесконечности приучили
древних греков к осторожности
(парадокс Зенона о том, что стрела не
может сдвинуться с места, Ахиллес никогда не догонит черепаху)Например: Евклид, формулировал свою знаменитую теорему о бесконечности простых чисел, выражается так: «Простых чисел существует больше всякого предложенного количества простых чисел», а бесконечно много или нет – об этом Евклид умалчивает.
Слайд 19 Основные заслуги в развитии теории множеств
принадлежат Г.
Кантору (родился в 1845 г в
Петербурге,
умер в 1918 г в Галле).Исследования бесконечных множеств
потребовало развития математической логики.
Первоначально эта область математики была очень далека
от практических приложений, но впоследствии её принципы составили идейную основу конструирования
электронных вычислительных машин и программирования вычислений на этих машинах.
Большой вклад в теорию множеств сделан трудами советских
математиков Н.Н.Лузина (1883 – 1950), П.С.Новикова, М.Я.
Суслина (1894 – 1919), П.С.Александрова, А.Н. Колмогорова и
др.
Тайны бесконечности (2)
Слайд 20Используемая литература
1. Виленкин Н.Я. «Рассказы о множествах»/ НАУКА главная редакция
физико-математической литературы: МОСКВА 1996
2. Сост. Никольская И.Л. Факультативный курс по
математике7–9 кл/ М: Просвещение /Блох А.Я. «Числовые множества»3. Нешков К.И. и др «Множества. Отношения. Числа. Величины.» Пособие для учителей/ М: Просвещение 1978