Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Объемы. Соотношения между единицами измерения объема
Содержание
- 1. Объемы. Соотношения между единицами измерения объема
- 2. Прозвенел и смолк звонок,Начинается урок.Друг на друга посмотрелиИ за парты дружно сели.
- 3. ПовторениеНайдите объем куба с ребром 4 см.(V=
- 4. Повторение Найдите площадь боковой поверхности куба с
- 5. ПовторениеБак для воды имеет форму прямоугольного параллелепипеда.
- 6. Проверка индивидуальной работыЗадание 1. Вычислить объем прямоугольного
- 7. Проверка индивидуальной работыЗадание 2. Вычислите площадь всей
- 8. Проверка индивидуальной работыЗадание 3. Вычисли площадь боковой
- 9. Прочитайте записи5 см, 8 дм³, 10 м,
- 10. Назовите единицы измерения объема1 см³= 1000 мм³1дм³=
- 11. Решение задач№827Длина аквариума 80 см, ширина 45
- 12. Анализ задачиЧто требуется найти в задаче?(В задачи
- 13. Анализ задачиНазовите три его измерения.(Длина 80 см,
- 14. Анализ задачиКакое есть дополнительное условие?(Нужно чтоб уровень
- 15. Решение:1) 55-10=45 (см) – высота уровня воды2)
- 16. Решение задачи№828Прямоугольный параллелепипед (рис. 88) разделен на
- 17. Анализ задачиРассмотрите первую картинку.Назовите три измерения прямоугольного
- 18. Анализ задачиКакие формулы мы будем использовать?(V=авс, S= 2ав+2вс+2ас)Вычислите объем и площадь поверхности.(V=8·10·6=480 см³S=10·6·2+8·10·2+6·8·2=120+160+96=376 см²)
- 19. Анализ задачиРассмотрите вторую и третью картинку и
- 20. Анализ задачиПроверьте, равен ли объем параллелепипеда сумма
- 21. Решение задачи№824Найдите объем куба, если площадь его поверхности равна 96 см².
- 22. Анализ задачиЧто известно в задаче?(В задаче известна
- 23. Анализ задачиСколько граней у куба?(У куба 6
- 24. Анализ задачиКакую формулу удобно использовать для вычисления
- 25. Подведение итогов урокаРасскажите, как запомнить соотношение единиц
- 26. Подведение итогов урокаНазовите формулы для вычисления объема.(V=авс – нахождение объема прямоугольного параллелепипедаV=а³ - нахождение объема куба)
- 27. Домашнее задание№841,№844, №846 (в,г)
- 28. Скачать презентанцию
Прозвенел и смолк звонок,Начинается урок.Друг на друга посмотрелиИ за парты дружно сели.
Слайды и текст этой презентации
Слайд 1Объемы. Соотношения между единицами измерения объема
Кудрина С.Н. учитель математики МБОУ
КГО СОШ№58 г. Камышлов
Слайд 3Повторение
Найдите объем куба с ребром 4 см.
(V= 4³=64 см³)
Найдите площадь
всей поверхности куба с ребром 4 см.
(S=4·4·6=96 см²)
Слайд 4Повторение
Найдите площадь боковой поверхности куба с ребром 4 см.
(S=4·4·4=64
см²)
Высота комнаты 3 м, ширина 5 м, а длина 6
м. Сколько кубических метров воздуха находится в комнате?(V=3·5·6=90 см³)
Слайд 5Повторение
Бак для воды имеет форму прямоугольного параллелепипеда. Его три измерения:
3 дм, 5 дм, 4 дм. Найдите объем бака для
воды. Сколько литров воды входит в этот бак?(V=3·5·4=60 дм³=60 л)
Слайд 6Проверка индивидуальной работы
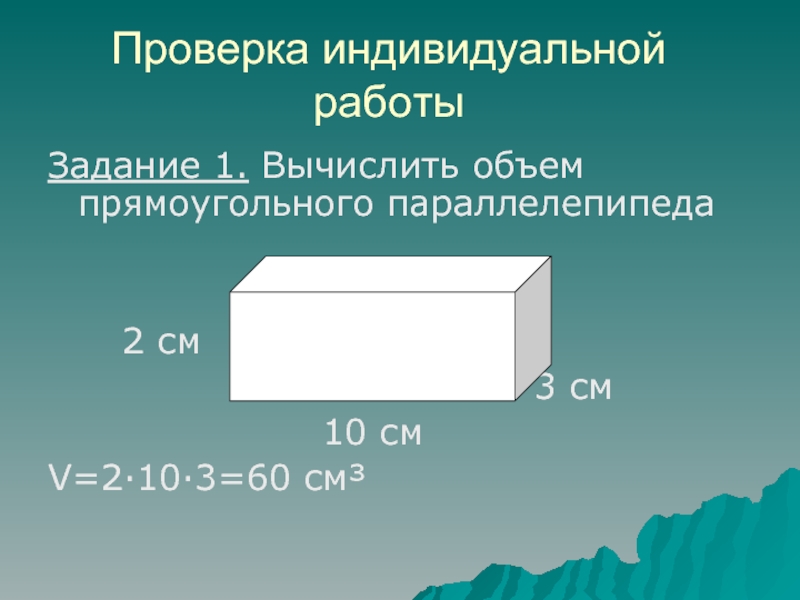
Задание 1. Вычислить объем прямоугольного параллелепипеда
2 см
3 см10 см
V=2·10·3=60 см³
Слайд 7Проверка индивидуальной работы
Задание 2. Вычислите площадь всей поверхности куба.
5
смS=5·5·6=150 см²
Слайд 8Проверка индивидуальной работы
Задание 3. Вычисли площадь боковой поверхности прямоугольного параллелепипеда.
5 см
2 см9 см
S=2·5·9+ 2·2·5=90+20=110 см²
Слайд 10Назовите единицы измерения объема
1 см³= 1000 мм³
1дм³= 1000 см³= 1
л
1м³= 1000 дм³= 1 000 000 см³
Слайд 11Решение задач
№827
Длина аквариума 80 см, ширина 45 см, а высота
55 см. Сколько литров воды надо влить в этот аквариум,
чтобы уровень воды был ниже верхнего края аквариума на 10 см.Слайд 12Анализ задачи
Что требуется найти в задаче?
(В задачи требуется найти сколько
литров воды входит в аквариум)
Какую форму имеет аквариум?
(Аквариум имеет форму
прямоугольного параллелепипеда)Слайд 13Анализ задачи
Назовите три его измерения.
(Длина 80 см, ширина 45 см,
высота 55 см)
Что нужно вычислить, чтобы узнать, сколько воды входит
в аквариум?(Чтобы узнать, сколько воды входит в аквариум надо вычислить его объем)
Слайд 14Анализ задачи
Какое есть дополнительное условие?
(Нужно чтоб уровень воды был ниже
верхнего края аквариума на 10 см)
Как вы это понимаете?
(Нужно высоту
уменьшить на 10 см)Слайд 15Решение:
1) 55-10=45 (см) – высота уровня воды
2) 80·45·45=162 000 (см³)
3)
162 000 см³ = 162 дм³ = 162 л
Ответ: в аквариум
надо влить 162 л воды. Слайд 16Решение задачи
№828
Прямоугольный параллелепипед (рис. 88) разделен на две части. Найдите
объем и площадь поверхности всего параллелепипеда и обеих его частей.
Равен ли объем параллелепипеда сумме объемов его частей? Можно ли это сказать о площадях их поверхностей? Объясните почему.Слайд 17Анализ задачи
Рассмотрите первую картинку.
Назовите три измерения прямоугольного параллелепипеда.
(Длина – 10
см, ширина – 6 см, высота – 8 см)
Можно ли
по этим данным вычислить объем и площадь поверхности?(Да)
Слайд 18Анализ задачи
Какие формулы мы будем использовать?
(V=авс, S= 2ав+2вс+2ас)
Вычислите объем и
площадь поверхности.
(V=8·10·6=480 см³
S=10·6·2+8·10·2+6·8·2=120+160+96=376 см²)
Слайд 19Анализ задачи
Рассмотрите вторую и третью картинку и аналогично вычислите объем
и площадь поверхности прямоугольного параллелепипеда.
(V1=8·3·6=144 см³
S1=3·6·2+3·8·2+8·6·2=36+48+96 =180 см²
V2=8·7·6=336 см³
S2=7·8·2+8·6·2+6·7·2=112+96+84
=292 см²)Слайд 20Анализ задачи
Проверьте, равен ли объем параллелепипеда сумма объемов его частей.
(V=V+V
144+336=480
см³)
Можно ли это сказать о площадях их поверхностей?
(S≠S+S
180+292=472 см², 376≠472)
Слайд 22Анализ задачи
Что известно в задаче?
(В задаче известна площадь поверхности куба)
Что требуется найти?
(Требуется найти объем куба)
Из чего складывается площадь
всей поверхности?(Площадь всей поверхности складывается из суммы площадей всех граней)
Слайд 23Анализ задачи
Сколько граней у куба?
(У куба 6 граней)
Что вы можете
о них сказать?
(Грани представляют собой 6 равных квадратов)
Как найти площадь
одной грани?(S=а²)
Слайд 24Анализ задачи
Какую формулу удобно использовать для вычисления объема?
V=S·с
1) 96:6=16(см²) –
площадь основания
2) 16·4=64 (см³)
Ответ: объем куба 64 см³.
Слайд 25Подведение итогов урока
Расскажите, как запомнить соотношение единиц измерения объема?
(Единицы измерения
объема кубические, значит, линейные единицы измерения возводим в куб)
Слайд 26Подведение итогов урока
Назовите формулы для вычисления объема.
(V=авс – нахождение объема
прямоугольного параллелепипеда
V=а³ - нахождение объема куба)
Теги