Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Объём многогранника
Содержание
- 1. Объём многогранника
- 2. Многогранник Многогранник – это
- 3. Многогранник называется выпуклым, если
- 4. Что такое в житейском
- 5. Многие значительные достижения
- 6. В общем
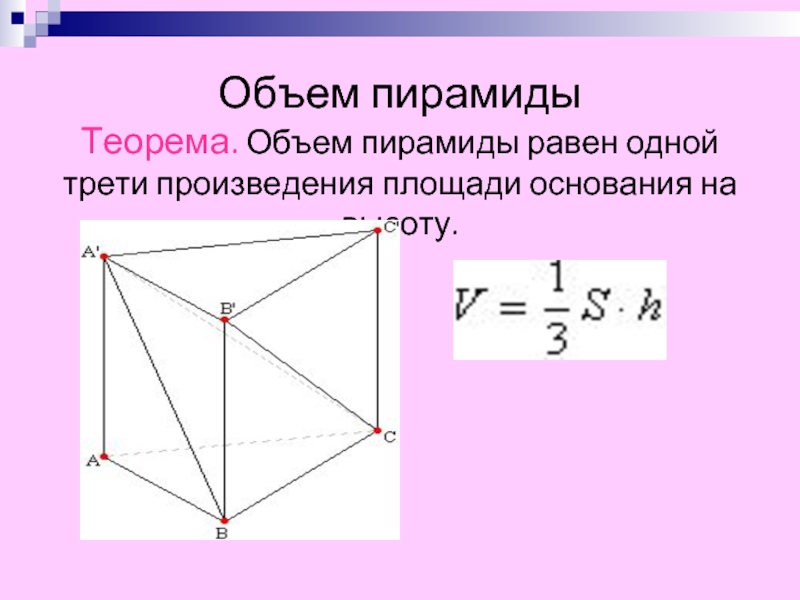
- 7. Объем пирамиды Теорема. Объем пирамиды равен одной трети произведения площади основания на высоту.
- 8. Объем многогранника Объем многогранника равен
- 9. Объем многогранника больше объема шара,
- 10. Площадь поверхности описанного многогранника
- 11. Скачать презентанцию
Многогранник Многогранник – это такое тело, поверхность которого состоит из конечного числа плоских многоугольников.
Слайды и текст этой презентации
Слайд 2 Многогранник
Многогранник – это такое тело,
поверхность которого состоит из конечного числа плоских многоугольников.
Слайд 3
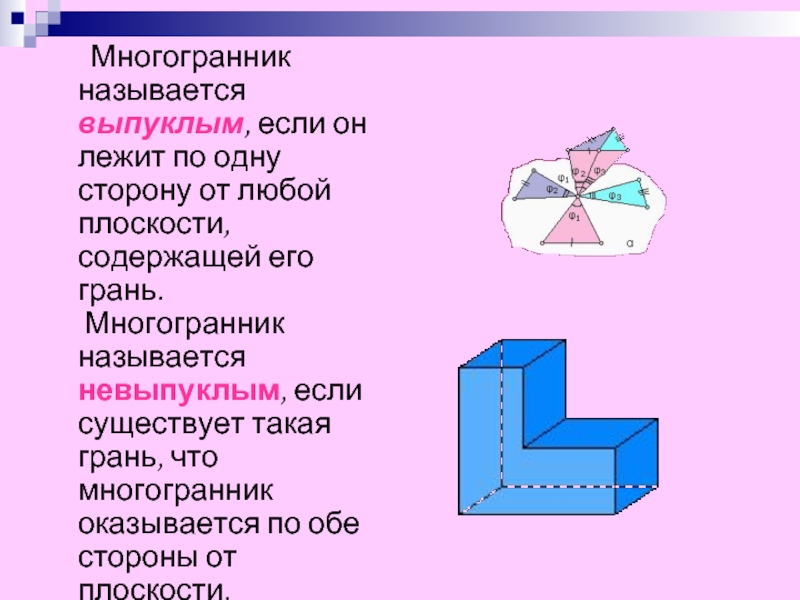
Многогранник называется выпуклым, если он лежит по
одну сторону от любой плоскости, содержащей его грань. Многогранник называется
невыпуклым, если существует такая грань, что многогранник оказывается по обе стороны от плоскости, содержащей эту грань.Слайд 4
Что такое в житейском смысле объем тела,
в частности многогранника? Это то, сколько жидкости может быть налито
внутрь этого многогранника. Отрежем вершинки и нальем внутрь каждого многогранника воду. Выпуклый многогранник уже наполнился, а невыпуклый — еще нет. Но возможно вода наливалась с разной скоростью: чтобы правильно сравнить объемы, выльем жидкость из каждого многогранника в одинаковые стаканы. Уровень воды в правом стакане выше, чем в левом, значит объем невыпуклого многогранника действительно больше объема выпуклого.Слайд 5
Многие значительные достижения математиков Древней Греции
в решении задач на нахождение кубатур (вычисление объемов) тел связаны
с применением метода исчерпывания, предположенным Евдоксом Книдским (около 408-355 до нашей эры).Известна формула, которая дает возможность найти объем многогранника, если известны лишь длины его ребер.
Объем произвольного многогранника можно вычислить, зная лишь длины его ребер. Однако многогранник должен быть специального вида.
Слайд 6
В общем случае можно показать,
что обобщённые объёмы многогранников — корни полиномиальных уравнений с коэффициентами,
которые не зависят от расположения вершин многогранника в пространстве, а представляют собой многочлены от квадратов длин его рёбер. Числовые коэффициенты этих многочленов определяются комбинаторным строением многогранника.Слайд 7 Объем пирамиды Теорема. Объем пирамиды равен одной трети произведения площади
основания на высоту.
Слайд 8Объем многогранника
Объем многогранника равен сумме объемов пирамид,
имеющих своими основаниями грани многогранника, а вершиной – центр сферы.
Так как все пирамиды имеют одну и ту же высоту, равную радиусу R сферы, то объем многогранника:Слайд 9
Объем многогранника больше объема шара, ограниченного сферой, но
меньше объема шара с тем же центром и с радиусом
R+ε. Таким образом,Слайд 10
Площадь поверхности описанного многогранника при неограниченном уменьшении
размеров его граней, т.е. при неограниченном уменьшении ε, стремится к
4πR^2 и поэтому эта величина принимается за площадь сферы.
Теги