Основные свойства функций

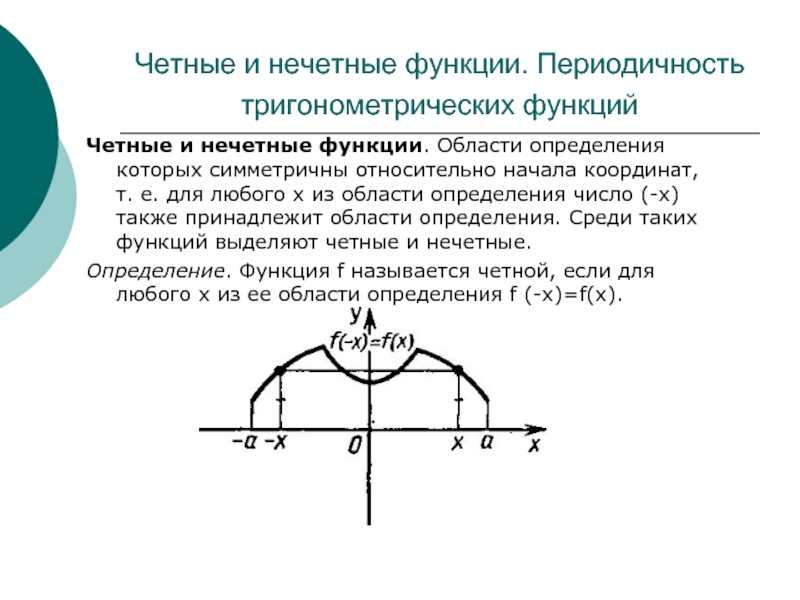
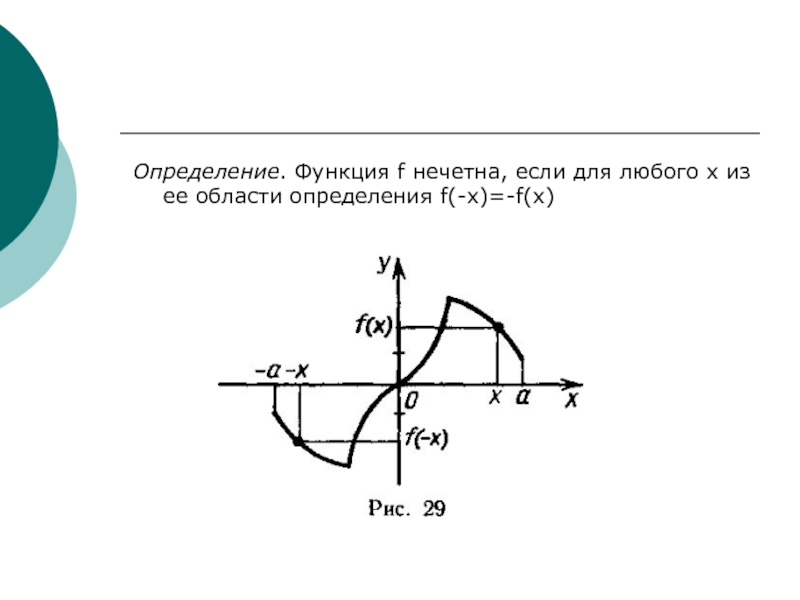
котором каждому числу х из множества D сопоставляется по некоторому

правилу число у, зависящее от х.
Функции обычно обозначают латинскими (а иногда греческими) буквами. Рассмотрим произвольную функцию f. Независимую переменную х называют также аргументом функции. Число у, соответствующее числу х, называют значением функции f в точке х и обозначают f (х). Область определения функции f обозна­чают D (f). Множество, состоящее из всех чисел f (х), таких, что х принадлежит области определения функции f, называют областью значений функции f и обозначают E(f).

Функции и их графики

элементов, которые принадлежат хотя бы одному из множеств А или

В.
Функции вида f(x)=p(x), где р(х) — многочлен, называют целыми рациональными функциями, а функции вида

где р и q — многочлены, называют дробно-рациональными функциями. Частное определено, если q (х) не обращается в нуль. Поэтому область определения дробно-рациональной функции множество всех действительных чисел, из которого m-iwnvj4cnDi корни многочлена q (х).

где y = f(x), а х «про­бегает» всю область определения

функции f.
Подмножество координатной плоскости является графиком какой-либо функции, если оно имеет не более одной общей точки с любой прямой, параллельной оси Оу.
Часто функцию задают графически. При этом для любого хо из области определения легко найти соответствующее значение yo =f(xo ) функции.

функции. Области определения которых симметричны относительно начала координат, т. е.

для любого х из области определения число (-х) также принадлежит области определения. Среди таких функций выделяют четные и нечетные.
Определение. Функция f называется четной, если для любого х из ее области определения f (-x)=f(x).

определения f(-x)=-f(x)

четной функции симметричен относительно оси ординат.
2. График нечетной функции симметричен

относительно начала координат.

Из этих двух правил вытекает следующее: при построении графика четной или нечетной функции достаточно построить его часть для неотрицательных х, а затем отразить полученный график относительно оси ординат (в случае четной функции) или начала координат (в случае нечетной).