Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Параллельные прямые в пространстве
Содержание
- 1. Параллельные прямые в пространстве
- 2. Цель урока:Дать учащимся систематические сведения о параллельных прямых в пространстве.
- 3. Знать и уметь:Основные свойства плоскости.Некоторые следствия из
- 4. Ход урока.Организационный момент.Учебники, тетради, инструменты.Основные задачи курса.
- 5. 2. Домашнее задание. Самостоятельная работа с последующей
- 6. В
- 7. 3. Новый материал: Расположение двух прямых в пространстве.Они
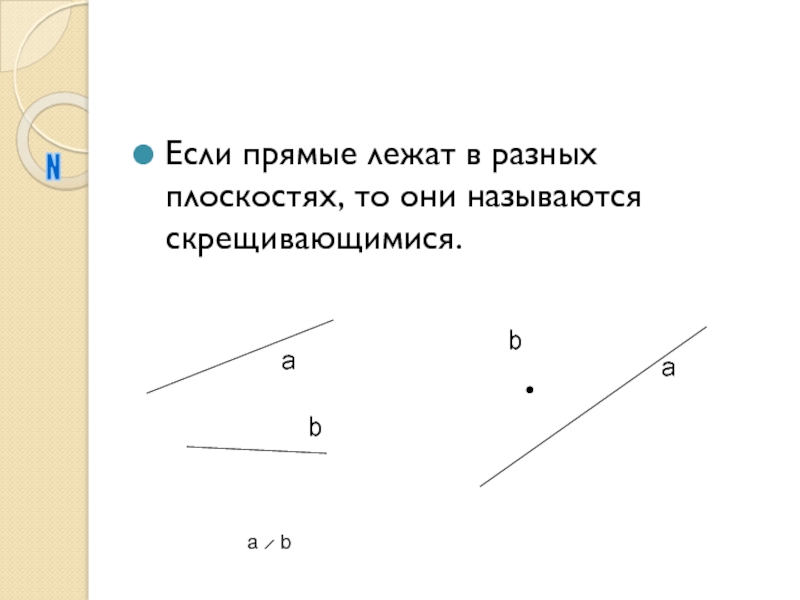
- 8. Если прямые лежат в разных плоскостях, то они называются скрещивающимися.Nbaabа ̷ b
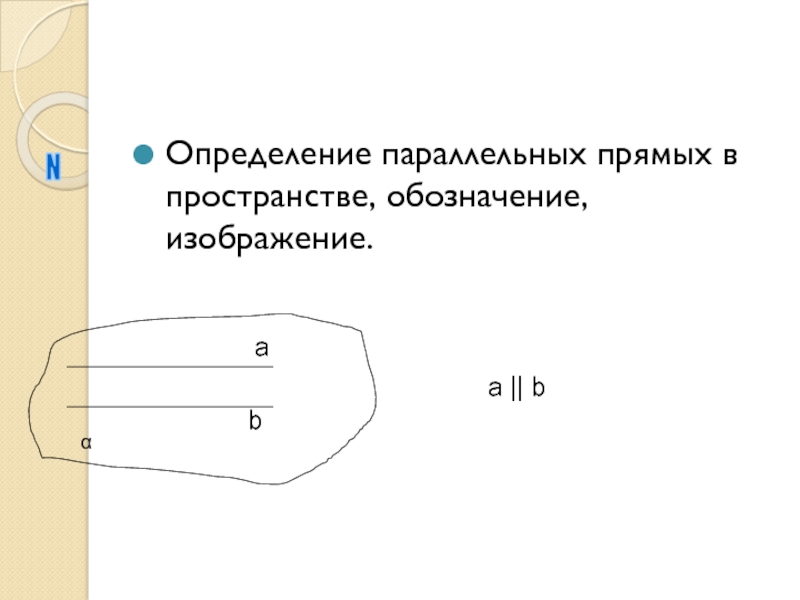
- 9. Определение параллельных прямых в пространстве, обозначение, изображение.Nbaαa || b
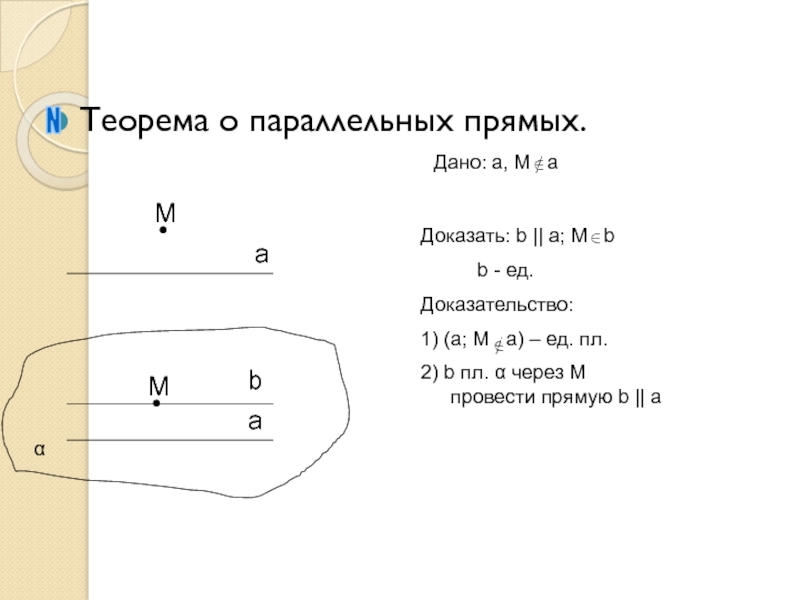
- 10. Теорема о параллельных прямых. NаaαMДано: a, M
- 11. Лемма о пересечении плоскости параллельными прямыми.(учебник стр.10)N
- 12. Теорема о трех параллельных прямых.Nabcbα1.M aДано: а
- 13. 4. Закрепление: задача №17
- 14. 6. Подведение итогов. Что узнали нового.7. Домашнее задание:П 4,5. №16,18,19,21.
- 15. Скачать презентанцию
Цель урока:Дать учащимся систематические сведения о параллельных прямых в пространстве.
Слайды и текст этой презентации
Слайд 3Знать и уметь:
Основные свойства плоскости.
Некоторые следствия из аксиом.
Взаимное расположение
двух прямых в пространстве.
трех параллельных прямых.
Слайд 52. Домашнее задание. Самостоятельная работа с последующей проверкой.
(тесты на парте.)
Тест №1 В 2 В 3
Слайд 73. Новый материал:
Расположение двух прямых в пространстве.
Они могут лежать в
одной плоскости или в разных. Если лежат в одной плоскости,
то они могут:А) совпадать В) пересекаться С) быть параллельными
N
a
b
a = b
M
b
a
a ⋂ b = M
a
b
a || b
Слайд 10Теорема о параллельных прямых.
N
а
a
α
M
Дано: a, M a
Доказать: b
|| a; M b
b - ед.
Доказательство:
1)
(a; M a) – ед. пл. 2) b пл. α через M провести прямую b || a
M
b
Слайд 12Теорема о трех параллельных прямых.
N
a
b
c
b
α
1.
M
a
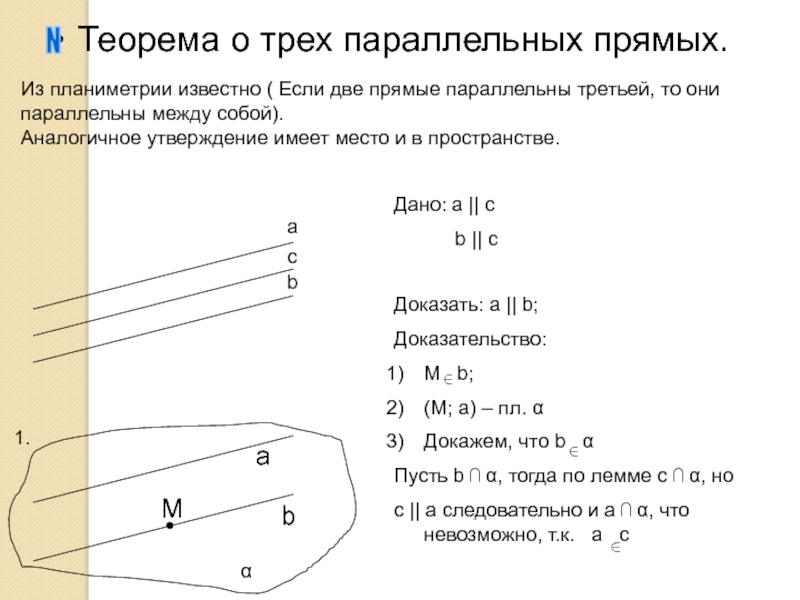
Дано: а || c
b || c
Доказать: a || b;
Доказательство:
M b;
(M; a) – пл. α
Докажем, что b α
Пусть b ⋂ α, тогда по лемме с ⋂ α, но
с || a следовательно и а ⋂ α, что невозможно, т.к. a c
Из планиметрии известно ( Если две прямые параллельны третьей, то они параллельны между собой).
Аналогичное утверждение имеет место и в пространстве.
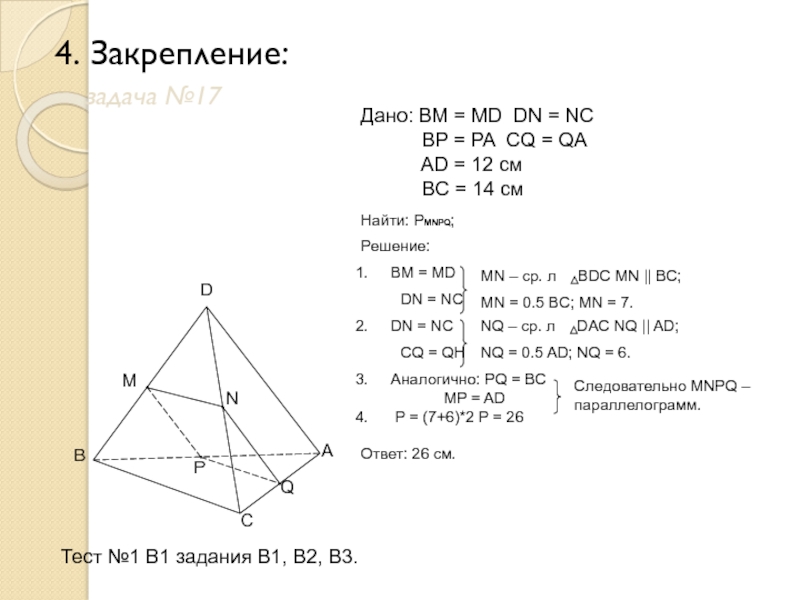
Слайд 134. Закрепление:
задача №17
B
M
D
C
A
N
P
Q
Дано: BM
= MD DN = NC
BP = PA CQ = QAAD = 12 см
BC = 14 см
Найти: PMNPQ;
Решение:
BM = MD
DN = NC
DN = NC
CQ = QH
Аналогично: PQ = BC
MP = AD
P = (7+6)*2 P = 26
Ответ: 26 см.
MN – ср. л BDC MN || BC;
MN = 0.5 BC; MN = 7.
NQ – ср. л DAC NQ || AD;
NQ = 0.5 AD; NQ = 6.
Следовательно MNPQ – параллелограмм.
Тест №1 В1 задания В1, В2, В3.
