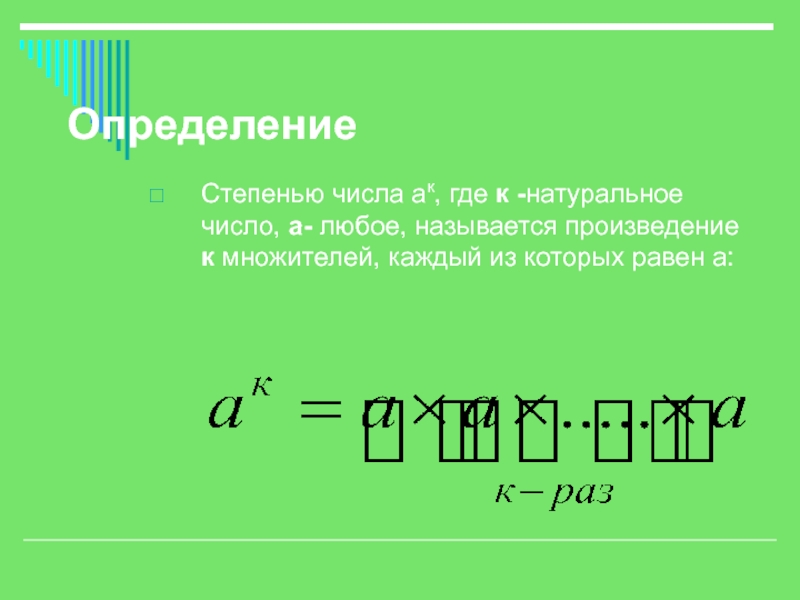
одночлена;
Стандартный вид одночлена.
Уметь:
Умножать степени;
Возводить в степень;
Делить степени;
Упрощать выражения, содержащие степень;
Умножать
одночлены;Возводить одночлены в степень.