Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Пирамида (10 класс)
Содержание
- 1. Пирамида (10 класс)
- 2. СодержаниеОпределение пирамидыПравильная пирамидаУсеченная пирамидаРешение задачИтог урокаСписок литературы
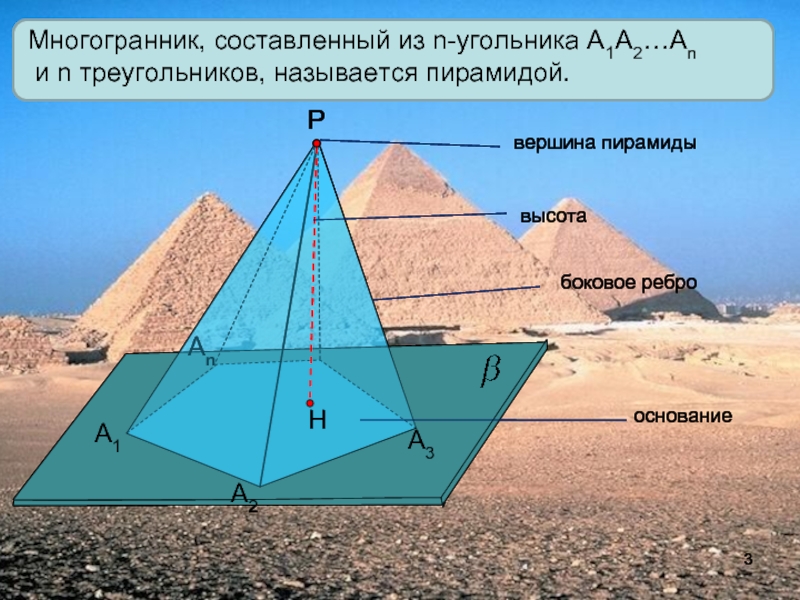
- 3. А1А2АnРА3Многогранник, составленный из n-угольника А1А2…Аn и n треугольников, называется пирамидой.вершина пирамидывысотабоковое реброоснование
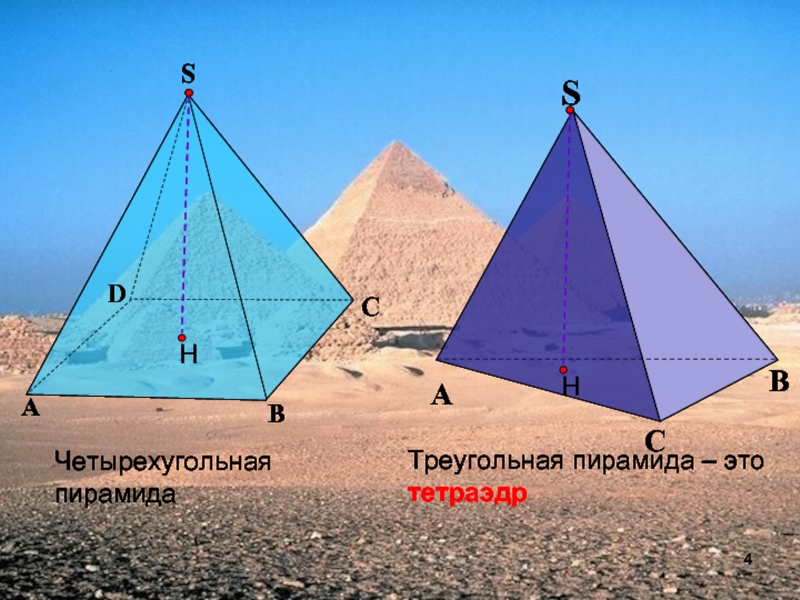
- 4. Треугольная пирамида – это тетраэдрЧетырехугольная пирамидаАBCDS
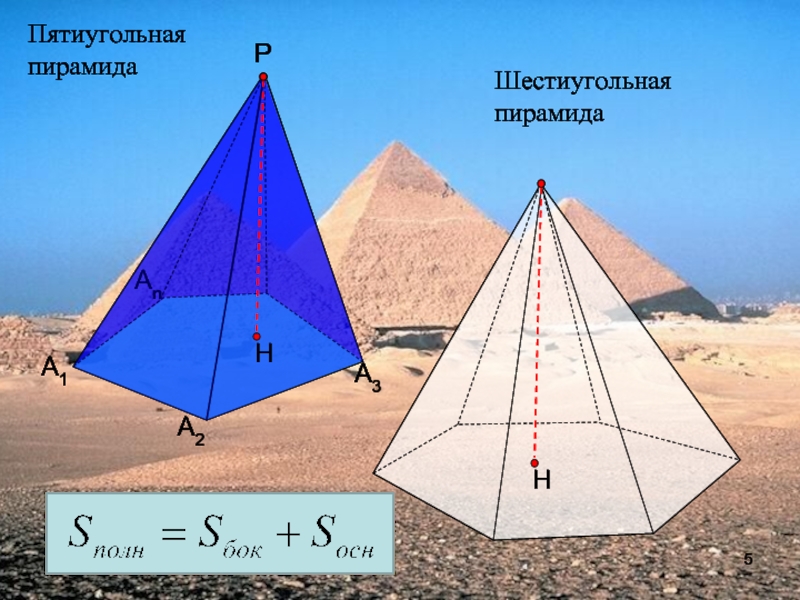
- 5. Пятиугольная пирамидаА1А2АnРА3Шестиугольная пирамида
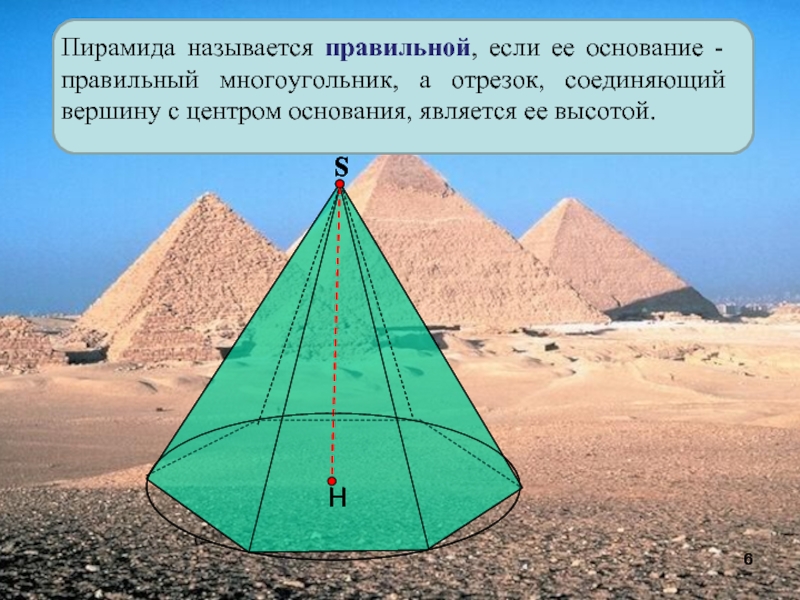
- 6. Пирамида называется правильной, если ее основание -
- 7. Все боковые ребра правильной пирамиды равны, а боковые грани являются равными равнобедренными треугольниками.А1А2А3А4А5А6S
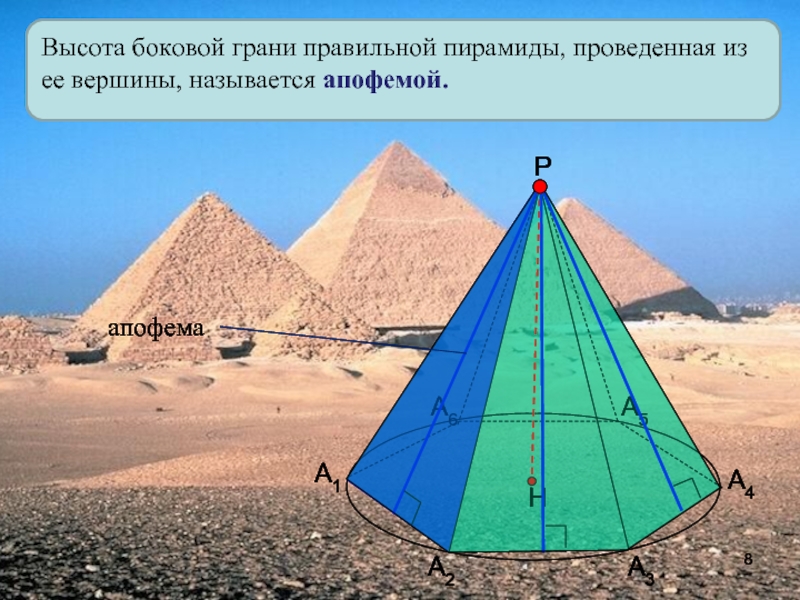
- 8. Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой.А1А2А3А4А5А6Рапофема
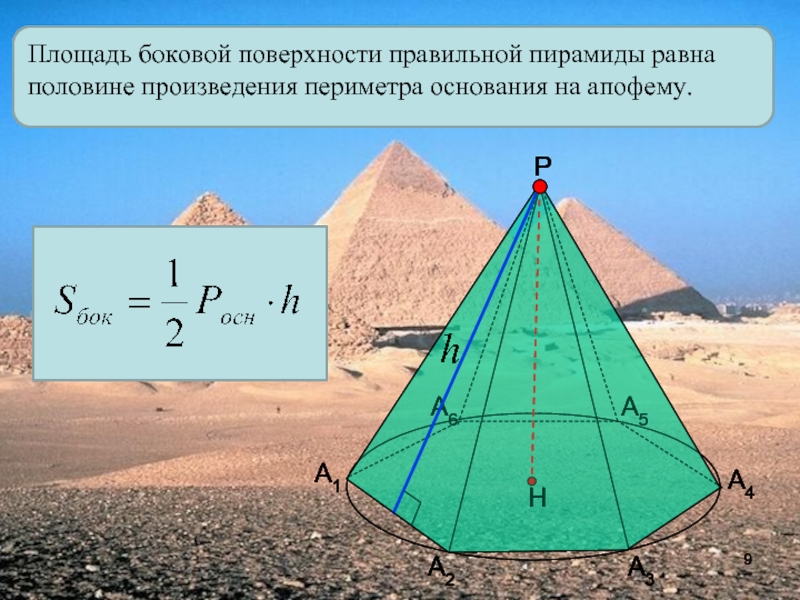
- 9. Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.А1А2А3А4А5А6Р
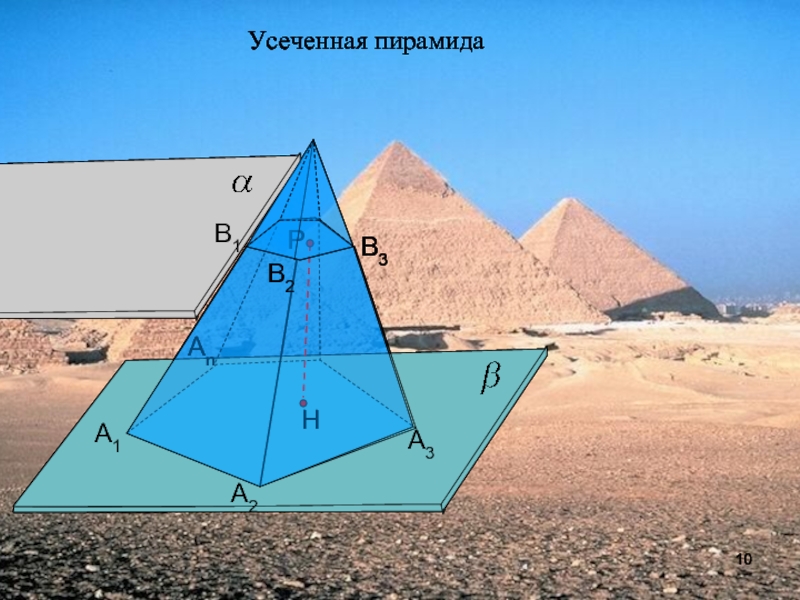
- 10. А1А2АnА3Усеченная пирамида
- 11. САВН № 239. Основанием пирамиды является ромб,
- 12. СВАD
- 13. Что называется пирамидой?Правильной пирамидой?Что называется площадью боковой
- 14. Подведение итогов. Домашнее задание.П.32,33,34№241,242
- 15. Список литературыАтанасян Л.С., Бутузов В.Ф.и др.Геометрия 10-11,Москва
- 16. Скачать презентанцию
СодержаниеОпределение пирамидыПравильная пирамидаУсеченная пирамидаРешение задачИтог урокаСписок литературы
Слайды и текст этой презентации
Слайд 1Урок математики в 10 классе по теме «Пирамида»
подготовила учитель математики
г.Нижнекамска РТ
Слайд 2Содержание
Определение пирамиды
Правильная пирамида
Усеченная пирамида
Решение задач
Итог урока
Список литературы
Слайд 3А1
А2
Аn
Р
А3
Многогранник, составленный из n-угольника А1А2…Аn
и n треугольников, называется
пирамидой.
вершина пирамиды
высота
боковое ребро
основание
Слайд 6Пирамида называется правильной, если ее основание - правильный многоугольник, а
отрезок, соединяющий вершину с центром основания, является ее высотой.
S
Слайд 7Все боковые ребра правильной пирамиды равны, а боковые грани являются
равными равнобедренными треугольниками.
А1
А2
А3
А4
А5
А6
S
Слайд 8Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется
апофемой.
А1
А2
А3
А4
А5
А6
Р
апофема
Слайд 9Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания
на апофему.
А1
А2
А3
А4
А5
А6
Р
Слайд 11С
А
В
Н
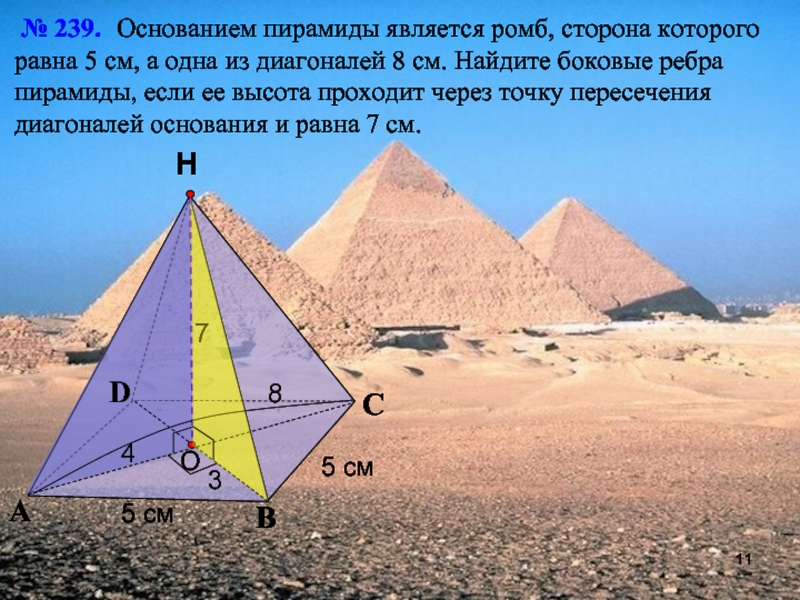
№ 239. Основанием пирамиды является ромб, сторона которого равна
5 см, а одна из диагоналей 8 см. Найдите боковые
ребра пирамиды, если ее высота проходит через точку пересечения диагоналей основания и равна 7 см.O
D
5 см
5 см
7
4
3
Слайд 12С
В
А
D
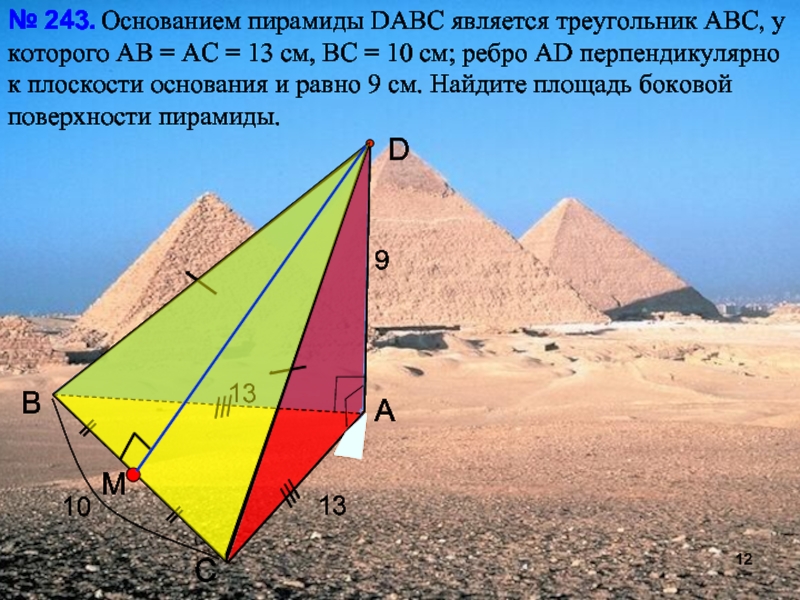
Основанием пирамиды DАВС
является треугольник АВС, у которого АВ = АС = 13
см, ВС = 10 см; ребро АD перпендикулярно к плоскости основания и равно 9 см. Найдите площадь боковой поверхности пирамиды.№ 243.
13
9
10
13
Слайд 13Что называется пирамидой?
Правильной пирамидой?
Что называется площадью боковой поверхности пирамиды?
Что называется
площадью полной поверхности пирамиды?
Чему равна площадь боковой поверхности правильной пирамиды?
Как
найти радиусы вписанной и описанной окружностей для произвольного треугольника?Формула для площади треугольника?
Итог урока
Слайд 15Список литературы
Атанасян Л.С., Бутузов В.Ф.и др.Геометрия 10-11,Москва «Просвещение»,2010
Яровенко В.А.
Поурочные разработки по геометрии. Дифференцированный подход. Москва «Вако»,2011
Теги