Решение геометрических заданий С4 ЕГЭ 2014

г.Бугульма, 2014г.
Презентацию выполнил: Чернобровкин А., ученик 11 класса МБОУ СОШ

МБОУ средняя общеобразовательная школа №9

по материалам ЕГЭ – 2014

наглядный),
дать характеристику фигуре, вспомнить определение, свойства, признаки,
определить зависимости между элементами,
рассуждать

Рекомендации при решении задач по геометрии:

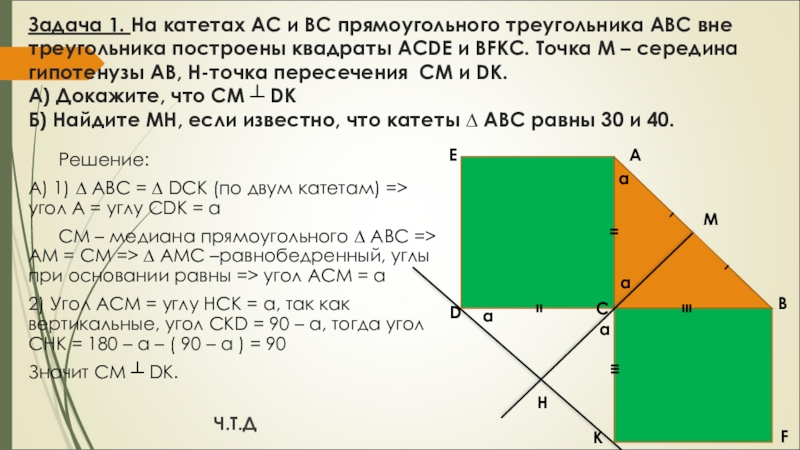
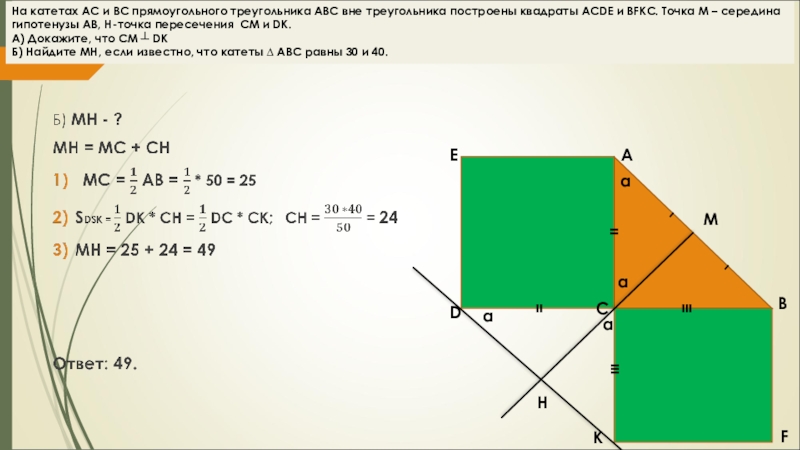
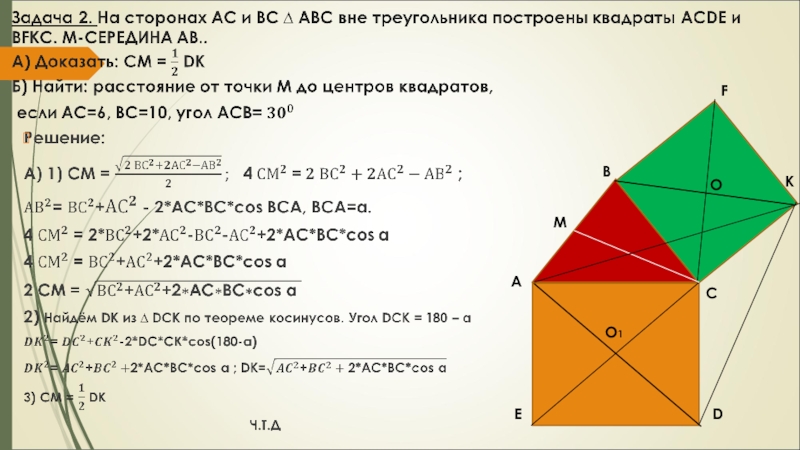
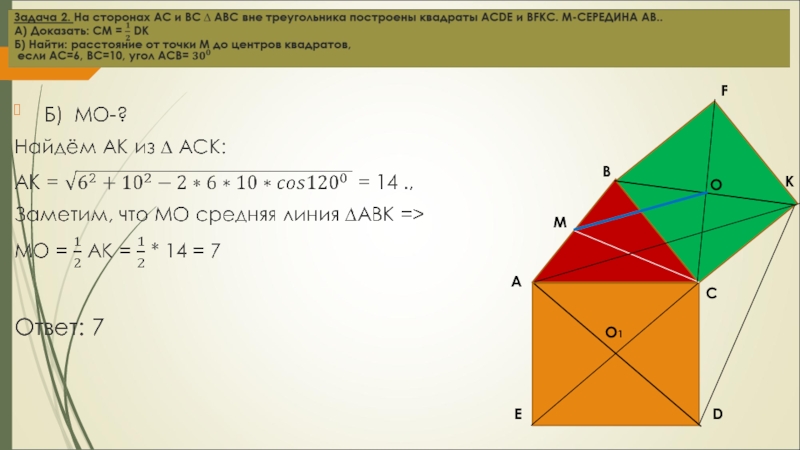
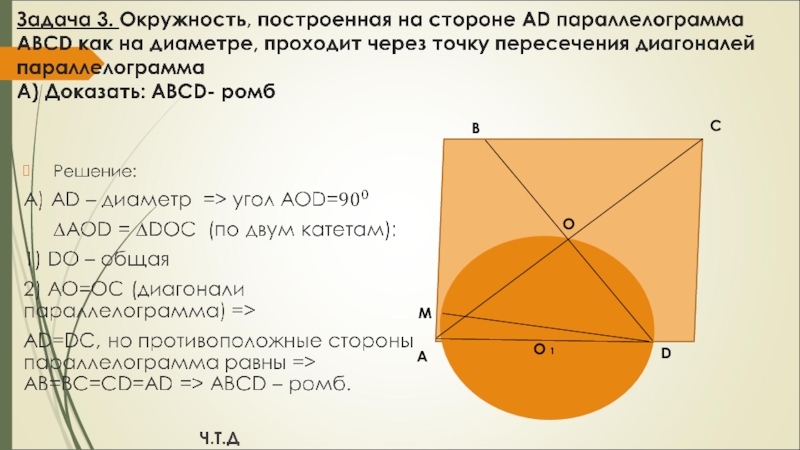
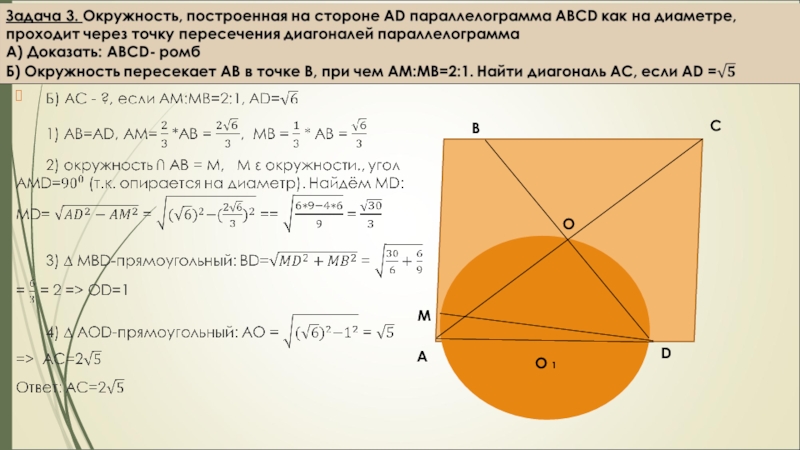
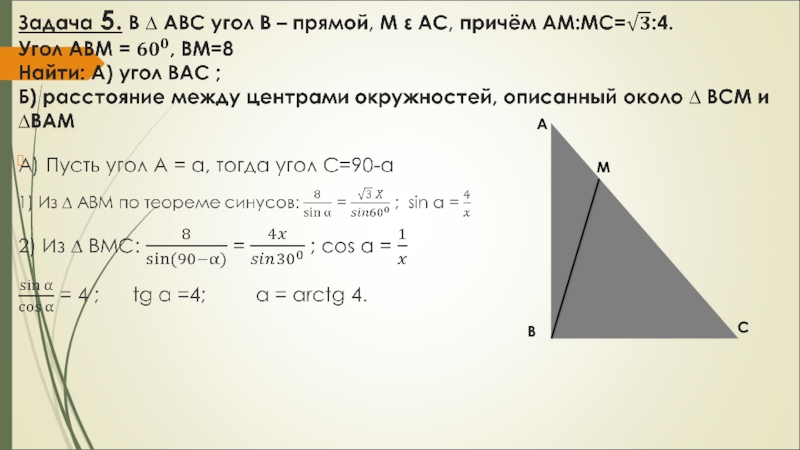
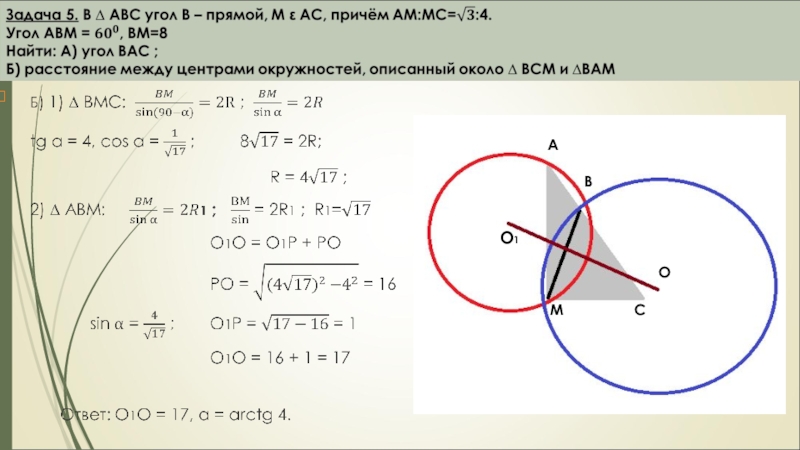
вне треугольника построены квадраты ACDE и BFKC. Точка М –

Решение:
А) 1) ∆ ABC = ∆ DCK (по двум катетам) => угол А = углу CDK = α
CM – медиана прямоугольного ∆ АВС => AM = CM => ∆ AMC –равнобедренный, углы при основании равны => угол ACM = α
2) Угол ACM = углу HCK = α, так как вертикальные, угол CKD = 90 – α, тогда угол CHK = 180 – α – ( 90 – α ) = 90
Значит CM ┴ DK.

Ч.Т.Д

A

B

C

E

D

M

F

K

H

α

α

α

α

=

=

-

-

≡

≡

вне треугольника построены квадраты ACDE и BFKC. Точка М –

пересекающая стороны АВ и АС в точках К и М. А)

С

B

A

M

K

вариантов заданий. Под ред. Семенова А.Л., Ященко И.В., М.: Экзамен,