Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ПЛОЩАДИ ПОВЕРХНОСТЕЙ ТЕЛ ВРАЩЕНИЯ ( ОБОБЩАЮЩИЙ УРОК)
Содержание
- 1. ПЛОЩАДИ ПОВЕРХНОСТЕЙ ТЕЛ ВРАЩЕНИЯ ( ОБОБЩАЮЩИЙ УРОК)
- 2. ПЛАН УРОКА:1. ОРГАНИЗАЦИОННЫЙ МОМЕНТ2.ПРЕЗЕНТАЦИИ ПО ТЕМАМ:3.ОБОБШЕНИЕ ТЕМа)
- 3. Тела вращенияТела вращения — объёмные тела, возникающие
- 4. Слайд 4
- 5. ЦилиндрЦилиндр (Прямой круговой цилиндр) – это тело,
- 6. Радиус цилиндра – это радиус его оснований.Ось
- 7. Круговой цилиндрКруговой цилиндр – тело, которое состоит
- 8. Сечения цилиндраСечение Цилиндра Плоскостью, Параллельной Его Оси, Представляет Прямоугольник.
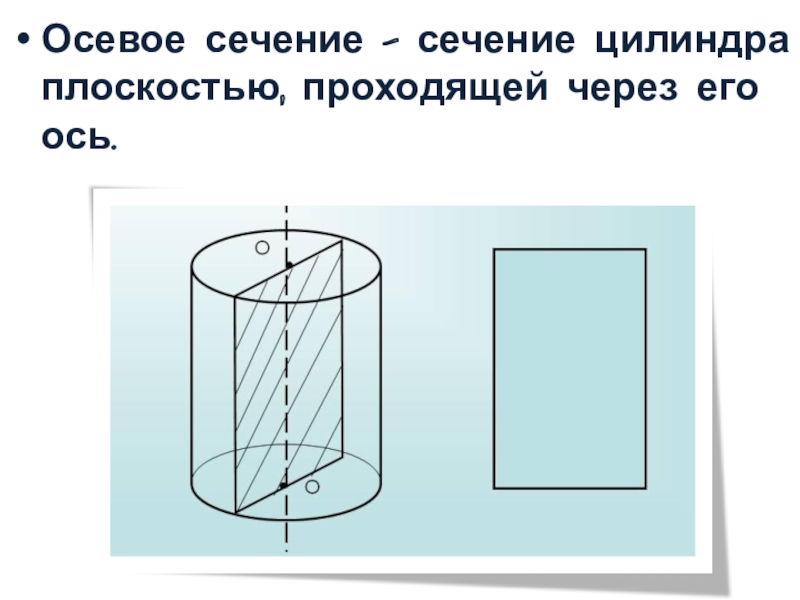
- 9. Осевое сечение – сечение цилиндра плоскостью, проходящей через его ось.
- 10. Сечение цилиндра плоскостью, параллельной основаниям и перпендикулярной к оси цилиндра, представляет собой круг.
- 11. Сечением цилиндра плоскостью, не являющейся перпендикулярной его
- 12. Слайд 12
- 13. Фигуры ВРАЩЕНИЯКонус.Усеченный КОНУС
- 14. Ко́нус (от др.-греч. κώνος «шишка») — тело
- 15. Отрезок, соединяющий вершину и границу основания, называется
- 16. Конус,основанием которого является круг,а основание высоты лежит
- 17. Площадью боковой поверхности конуса называется предел последовательности
- 18. Усеченным конусом называется часть конуса, заключенная между
- 19. Часть образующей полного конуса,заключенная между основаниями усеченного
- 20. Площадь боковой поверхности усеченного конуса вычисляется по
- 21. Геометрия 11 классПрезентация ученика 11р3 класса Сафарли ЭминаПрезентация по теме: Тела вращения
- 22. Сфера (шар)Шар – геометрическое тело, ограниченное поверхностью, все
- 23. Шаровой сегмент – это часть шара, отсекаемая
- 24. Формула площади поверхности шара:Формула площади поверхности шарового
- 25. 1. Тела вращения - объёмные тела, возникающие
- 26. цилиндр1.ВЫСОТА ЦИЛИНДРА 20 СМ , РАДИУС ОСНОВАНИЯ
- 27. конусСЕЧЕНИЕ ЦИЛИНДРА ПЛОСКОСТЬЮ С ПЛОЩАДЬЮ 80 СМ2
- 28. сфера1.В ЦИЛИНДРЕ С РАДИУСОМ ОСНОВАНИЯ 5 СМ
- 29. ВОПРОС 1
- 30. ВОПРОС 2
- 31. ВОПРОС 3
- 32. Слайд 32
- 33. Слайд 33
- 34. 4
- 35. Задача-4Найти площадь поверхности шара, вписанного в пирамиду
- 36. Слайд 36
- 37. Слайд 37
- 38. ДОМАШНЕЕ ЗАДАНИЕПО УЧЕБНИКУ :№ 330, 340, 359, 369 Благодарю за внимание .
- 39. Скачать презентанцию
ПЛАН УРОКА:1. ОРГАНИЗАЦИОННЫЙ МОМЕНТ2.ПРЕЗЕНТАЦИИ ПО ТЕМАМ:3.ОБОБШЕНИЕ ТЕМа) ОБЩИЕ СВОЙСТВА ДАННЫХ ТЕЛ б) РАБОТА В ГРУППАХс) ЗАДАЧИ ПОВЫШЕННОЙ ТРУДНОСТИ4. ПОДВЕДЕНИЕ ИТОГОВ5.ДОМАШНЕЕ ЗАДАНИЕ.ЦИЛИНДРКОНУСЦИЛИНДРСФЕРА
Слайды и текст этой презентации
Слайд 2ПЛАН УРОКА:
1. ОРГАНИЗАЦИОННЫЙ МОМЕНТ
2.ПРЕЗЕНТАЦИИ ПО ТЕМАМ:
3.ОБОБШЕНИЕ ТЕМ
а) ОБЩИЕ СВОЙСТВА ДАННЫХ
ТЕЛ
б) РАБОТА В ГРУППАХ
с) ЗАДАЧИ ПОВЫШЕННОЙ
ТРУДНОСТИ
4. ПОДВЕДЕНИЕ ИТОГОВ
5.ДОМАШНЕЕ
ЗАДАНИЕ.ЦИЛИНДР
КОНУС
ЦИЛИНДР
СФЕРА
Слайд 3Тела вращения
Тела вращения — объёмные тела, возникающие при вращении плоской
геометрической фигуры, ограниченной кривой, вокруг оси, лежащей в той же
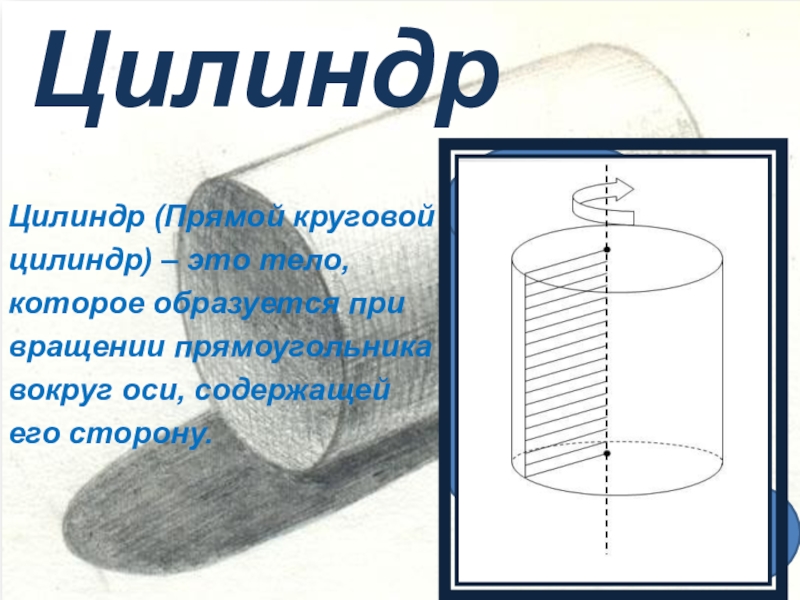
плоскости
Слайд 5Цилиндр
Цилиндр (Прямой круговой цилиндр) – это тело, которое образуется при
вращении прямоугольника вокруг оси, содержащей его сторону.
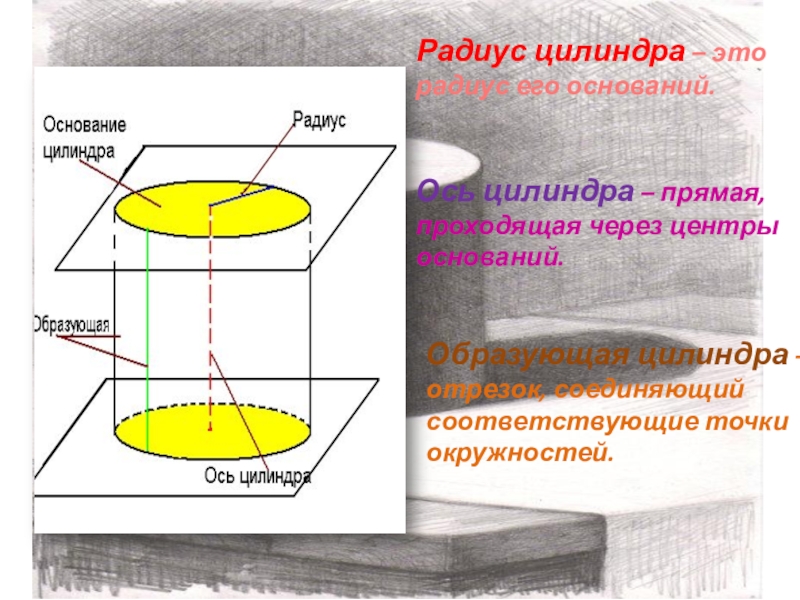
Слайд 6Радиус цилиндра – это радиус его оснований.
Ось цилиндра – прямая,
проходящая через центры оснований.
Образующая цилиндра – отрезок, соединяющий соответствующие точки
окружностей.
Слайд 7Круговой цилиндр
Круговой цилиндр – тело, которое состоит из двух равных
кругов, лежащих в параллельных плоскостях, и всех отрезков, соединяющих соответствующие
точки этих кругов.Высота цилиндра– расстояние между плоскостями оснований.
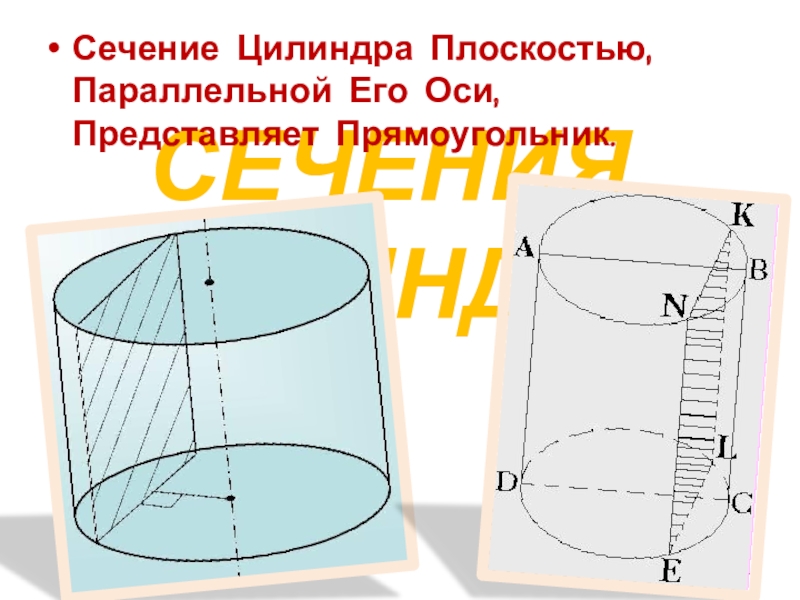
Слайд 8Сечения цилиндра
Сечение Цилиндра Плоскостью, Параллельной Его Оси, Представляет Прямоугольник.
Слайд 10Сечение цилиндра плоскостью, параллельной основаниям и перпендикулярной к оси цилиндра,
представляет собой круг.
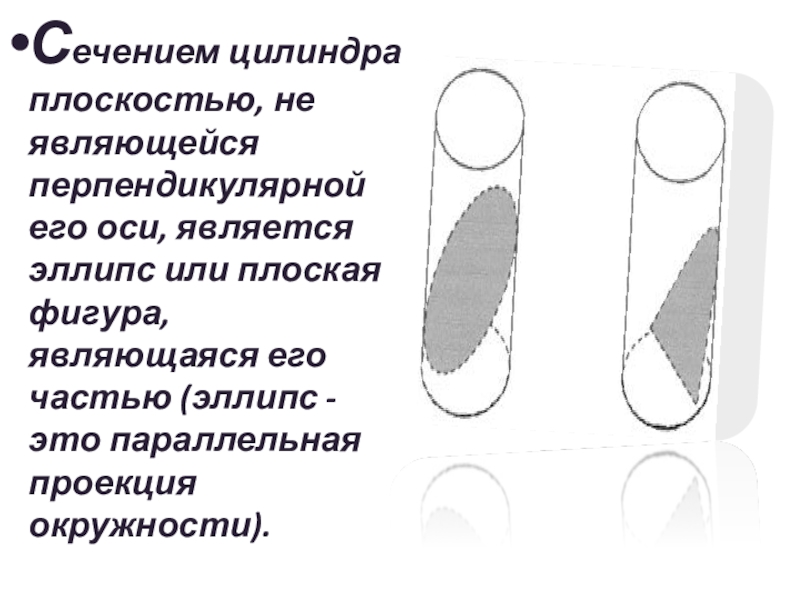
Слайд 11Сечением цилиндра плоскостью, не являющейся перпендикулярной его оси, является эллипс
или плоская фигура, являющаяся его частью (эллипс - это параллельная
проекция окружности).
Слайд 14Ко́нус (от др.-греч. κώνος «шишка») — тело в евклидовом пространстве,
полученное объединением всех лучей, исходящих из одной точки (вершины конуса)
и проходящих через плоскую поверхность. Конус- это тело полученное в результате вращения прямоугольного треугольника, относительно одного из его катетов.
Слайд 15Отрезок, соединяющий вершину и границу основания, называется образующей конуса.
Объединение образующих
конуса называется образующей (или боковой) поверхностью конуса. Образующая поверхность конуса
является конической поверхностью.Отрезок, опущенный перпендикулярно из вершины на плоскость основания (а также длина такого отрезка), называется высотой конуса.
Радиус основания конуса называется радиусом конуса.
Слайд 16Конус,основанием которого является круг,а основание высоты лежит в центре этого
круга,называется прямым круговым конусом.
Конус,осевым сечением которого является равносторонний треугольник,называется равносторонним
конусом.
Слайд 17Площадью боковой поверхности конуса называется предел последовательности площадей боковых поверхностей,вписанных
в него правильных пирамид и неограниченном увеличении числа сторон их
оснований и вычисляется по формуле:Sбок=¶RL
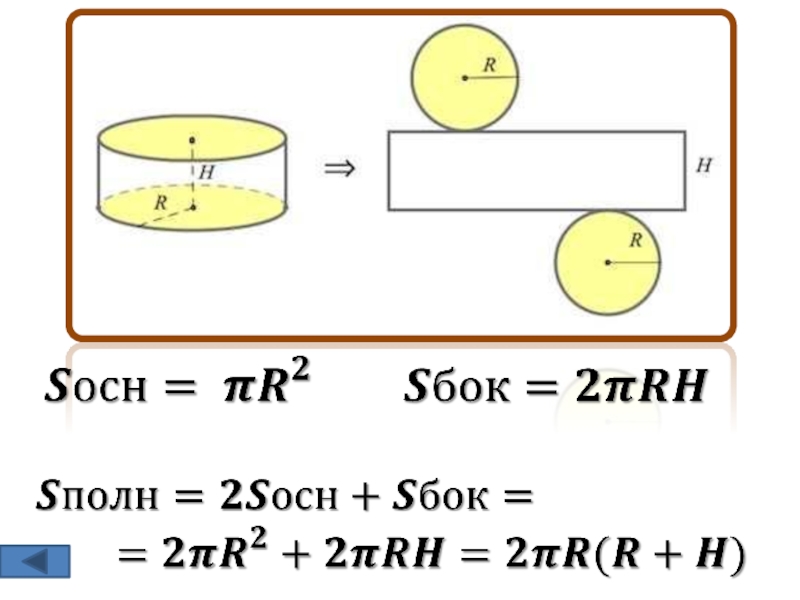
Сумма площадей боковой поверхности и основания есть площадь полной поверхности конуса:
Sпол=¶RL+¶R²
Здесь R – радиус основания конуса, L – его образующая
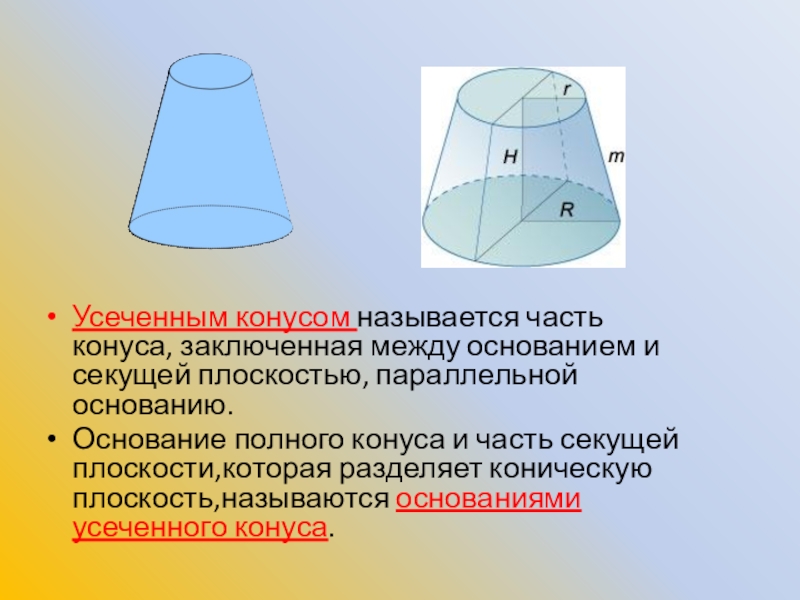
Слайд 18Усеченным конусом называется часть конуса, заключенная между основанием и секущей
плоскостью, параллельной основанию.
Основание полного конуса и часть секущей плоскости,которая разделяет
коническую плоскость,называются основаниями усеченного конуса.
Слайд 19Часть образующей полного конуса,заключенная между основаниями усеченного конуса,называется образующей усеченного
конуса.
Расстояние между плоскостями оснований называется высотой усеченного конуса.
Усеченный конус,являющийся частью
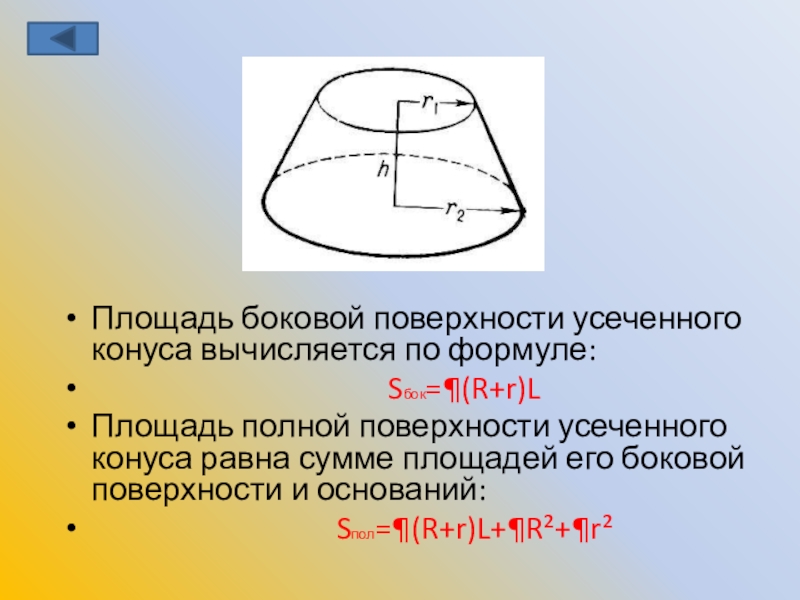
прямого кругового конуса,называется прямым круговым усеченным конусом.
Слайд 20Площадь боковой поверхности усеченного конуса вычисляется по формуле:
Sбок=¶(R+r)L
Площадь полной поверхности усеченного конуса равна сумме площадей его боковой поверхности и оснований:
Sпол=¶(R+r)L+¶R²+¶r²
Слайд 21Геометрия 11 класс
Презентация ученика 11р3 класса Сафарли Эмина
Презентация по теме:
Тела вращения
Слайд 22Сфера (шар)
Шар – геометрическое тело, ограниченное поверхностью, все точки которой находятся
на равном расстоянии от центра. Это расстояние называется радиусом шара.
Сфера – это поверхность шара. Сфера является телом вращения, образованным при вращении полуокружности вокруг своего диаметра. 
Слайд 23Шаровой сегмент – это часть шара, отсекаемая от него плоскостью.
Шаровой слой - часть шара, ограниченная двумя параллельными плоскостями, пересекающими
шар. Шаровой сектор — геометрическое тело, возникающее при вращении сектора вокруг одного из его радиусов(Ш. с. 1-го рода) или вокруг диаметра, не пересекающего его дуги (Ш. с. 2-го рода).
Слайд 24
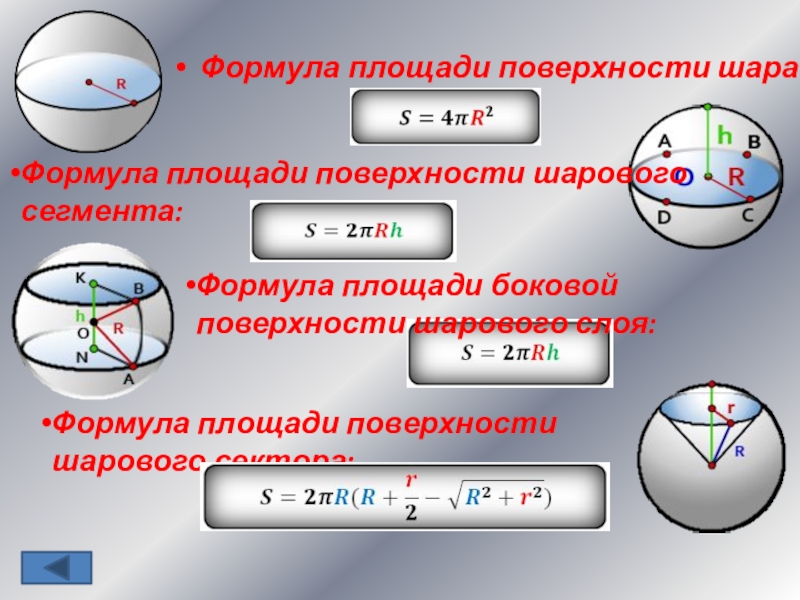
Формула площади поверхности шара:
Формула площади поверхности шарового сектора:
Формула площади боковой
поверхности шарового слоя:
Формула площади поверхности шарового сегмента:
Слайд 251. Тела вращения - объёмные тела, возникающие при вращении плоской
геометрической фигуры, ограниченной кривой, вокруг оси, лежащей в той же
плоскости.3.Что общего в формулах полной поверхности тел вращения?
1.Каким путём получаются тела вращения?
2.Какое из сечений одинаковое у всех трёх тел ?
2.Сечение ,перпендикулярное оси вращения.
Слайд 26цилиндр
1.ВЫСОТА ЦИЛИНДРА 20 СМ , РАДИУС ОСНОВАНИЯ 10 СМ. НАЙДИТЕ
ПЛОЩАДЬ СЕЧЕНИЯ, ПРОХОДЯЩЕГО ПАРАЛЛЕЛЬНО ОСИ ЦИЛИНДРА НА РАССТОЯНИИ 6 СМ.
2.
ОСЕВОЕ СЕЧЕНИЕ КОНУСА – ЭТО ТРЕУГОЛЬНИК С УГЛОМ ПРИ ВЕРШИНЕ В 90 ͦͦͦ. НАЙДИТЕ ОТНОЩЕНИЕ SБОК : SОСН .3. СФЕРА РАДИУСОМ 5 СМ КАСАЕТСЯ СТОРОН ТРЕУГОЛЬНИКА С ДЛИНАМИ 13 СМ, 14СМ И 15 СМ. НАЙДИТЕ РАССТОЯНИЕ ОТ ЦЕНТРА СФЕРЫ ДО ПЛОСКОСТИ ТРЕУГОЛЬНИКА.
Слайд 27конус
СЕЧЕНИЕ ЦИЛИНДРА ПЛОСКОСТЬЮ С ПЛОЩАДЬЮ 80 СМ2 ПРОВЕДЕНО ПАРАЛЛЕЛЬНО ОСИ
ЦИЛИНДРА С РАДИУСОМ 5 СМ И ВЫСОТОЙ 10 СМ. НАЙДИТЕ
РАССТОЯНИЕ ОТ СЕЧЕНИЯ ДО ОСИ ЦИЛИНДРА.2. ОСЕВОЕ СЕЧЕНИЕ КОНУСА – ЭТО ТРЕУГОЛЬНИК С УГЛОМ ПРИ ВЕРШИНЕ В 120 ͦͦ. НАЙДИТЕ ОТНОЩЕНИЕ SБОК : SОСН .
3. СФЕРА РАДИУСОМ 5 СМ КАСАЕТСЯ СТОРОН ТРЕУГОЛЬНИКА С ДЛИНАМИ 10 СМ, 10СМ И 12 СМ. НАЙДИТЕ РАССТОЯНИЕ ОТ ЦЕНТРА СФЕРЫ ДО ПЛОСКОСТИ ТРЕУГОЛЬНИКА
Слайд 28сфера
1.В ЦИЛИНДРЕ С РАДИУСОМ ОСНОВАНИЯ 5 СМ И ВЫСОТОЙ 10
СМ ПРОВЕДЕНО СЕЧЕНИЕ ПЛОСКОСТЬЮ , ПАРАЛЛЕЛЬНОЙ ОСИ ЦИЛИНДРА НА РАССТОЯНИИ
3 СМ ОТ ОСИ. НАЙДИТЕ ПЛОЩАДЬ СЕЧЕНИЯ.2. ОСЕВОЕ СЕЧЕНИЕ КОНУСА – ЭТО ТРЕУГОЛЬНИК С УГЛОМ ПРИ ВЕРШИНЕ В 60 ͦͦ. НАЙДИТЕ ОТНОЩЕНИЕ SБОК : SОСН .
3. СФЕРА РАДИУСОМ 5 СМ КАСАЕТСЯ СТОРОН ТРЕУГОЛЬНИКА С ДЛИНАМИ 15 СМ, 15СМ И 24 СМ. НАЙДИТЕ РАССТОЯНИЕ ОТ ЦЕНТРА СФЕРЫ ДО ПЛОСКОСТИ ТРЕУГОЛЬНИКА.
Слайд 35Задача-4
Найти площадь поверхности шара, вписанного в пирамиду в основании которой
лежит треугольник со сторонами 13см, 14см и 15 см, если
вершина пирамиды удалена от каждой стороны основания на 5 см.
