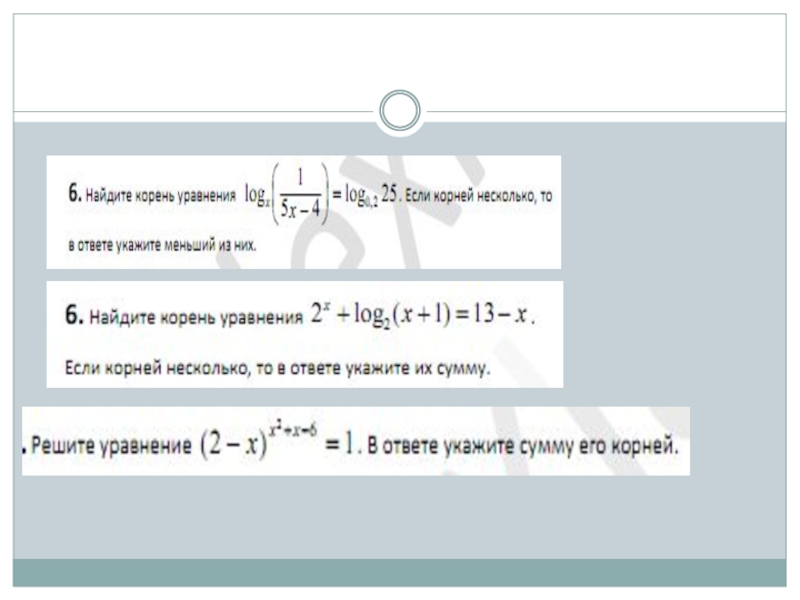
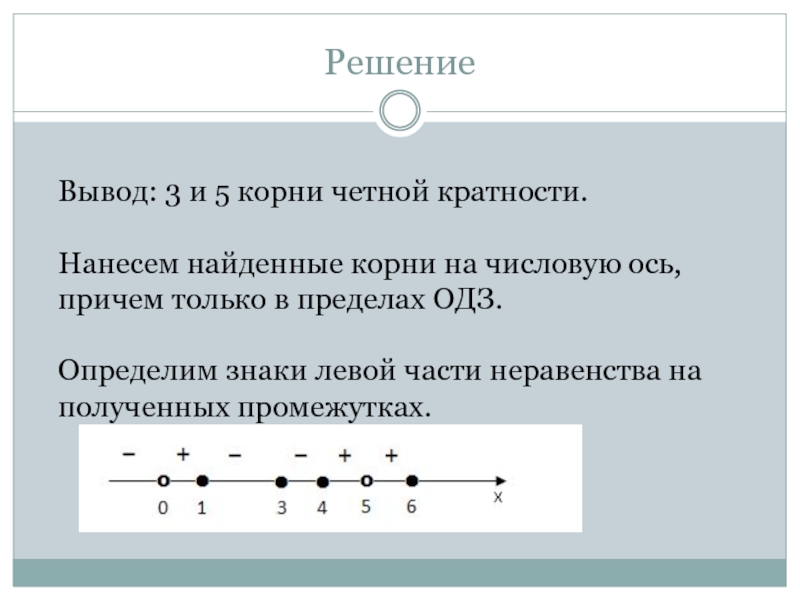
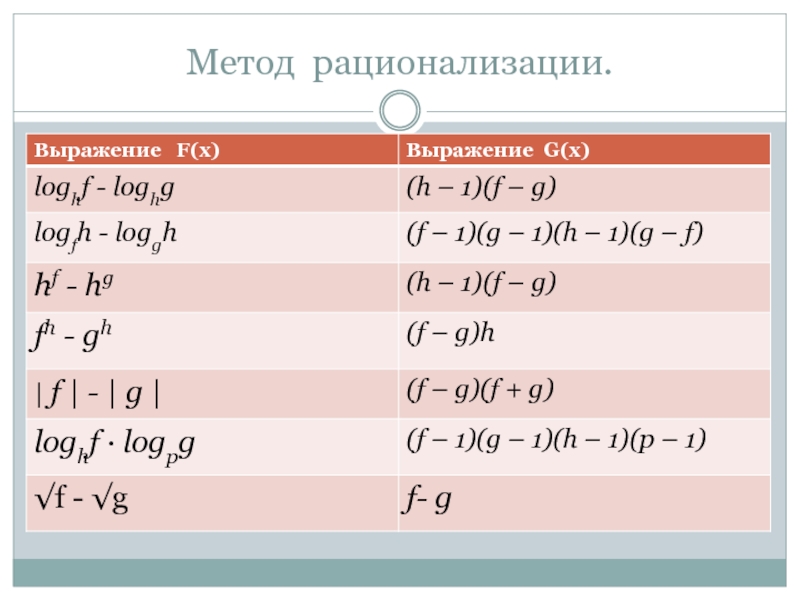
И ВПОСЛЕДСТВИИ ПОДТВЕРДИТЬ,
ЧТО, СЛЕДУЯ ЭТОМУ МЕТОДУ,
МЫ ДОСТИГНЕМ ЦЕЛИ.»
ЛЕЙБНИЦРазличные методы решения неравенств