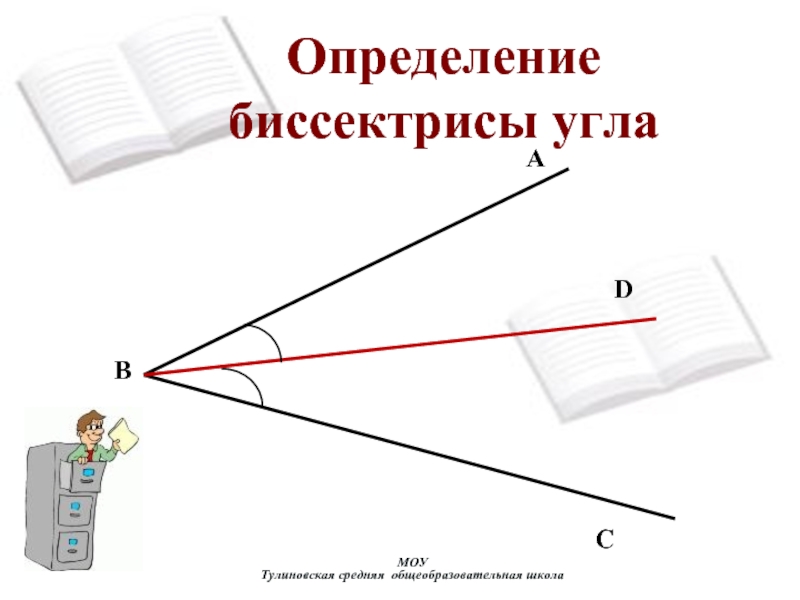
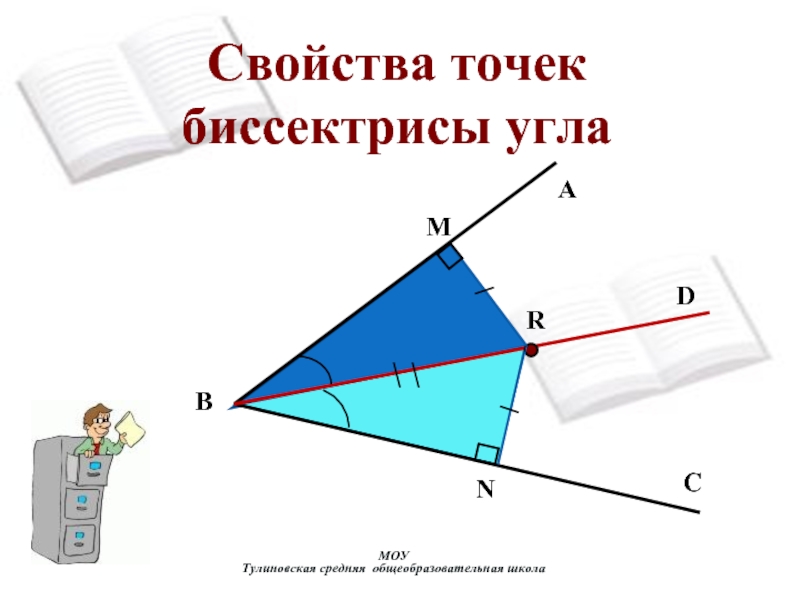
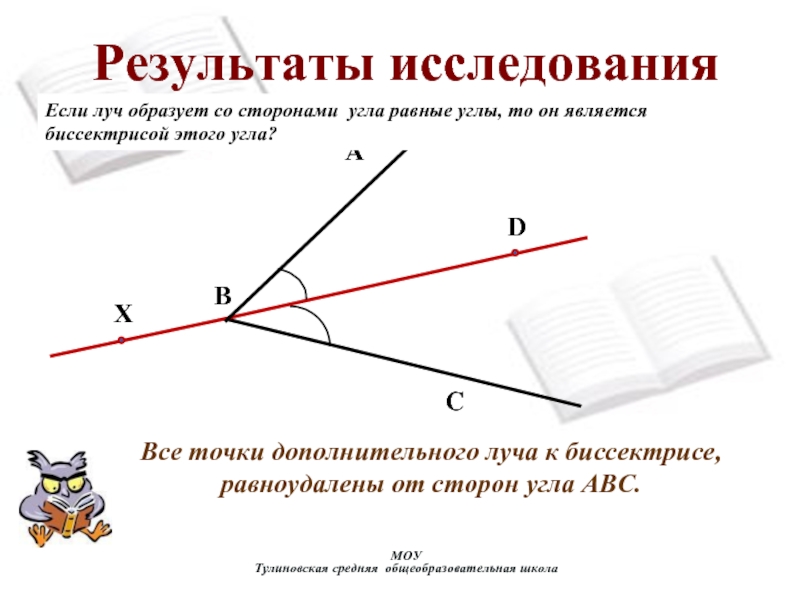
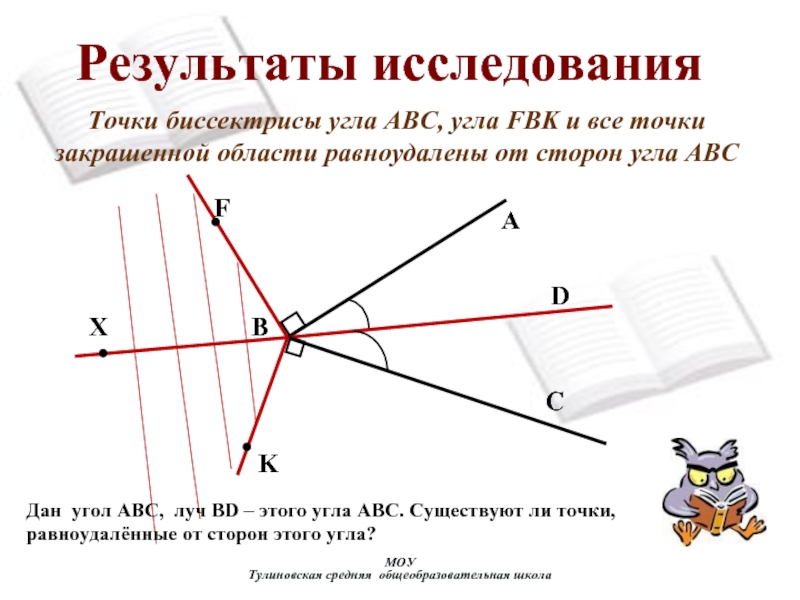
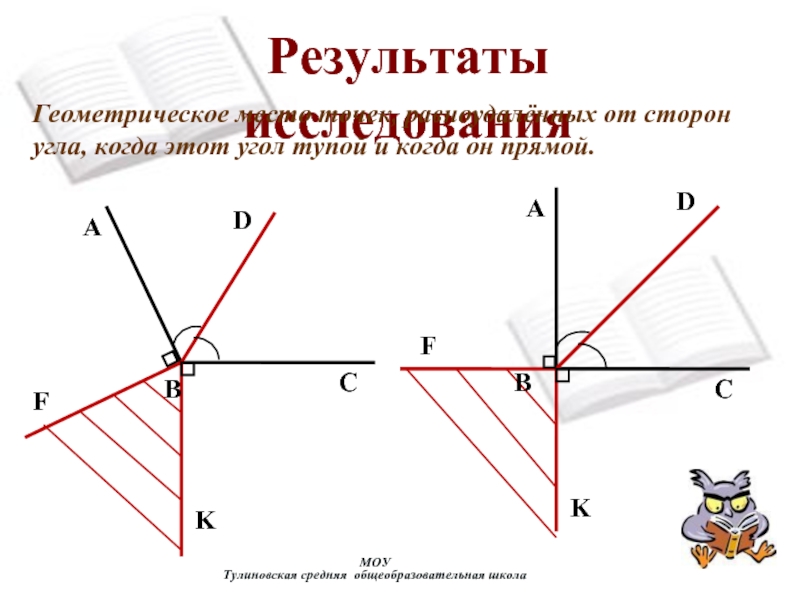
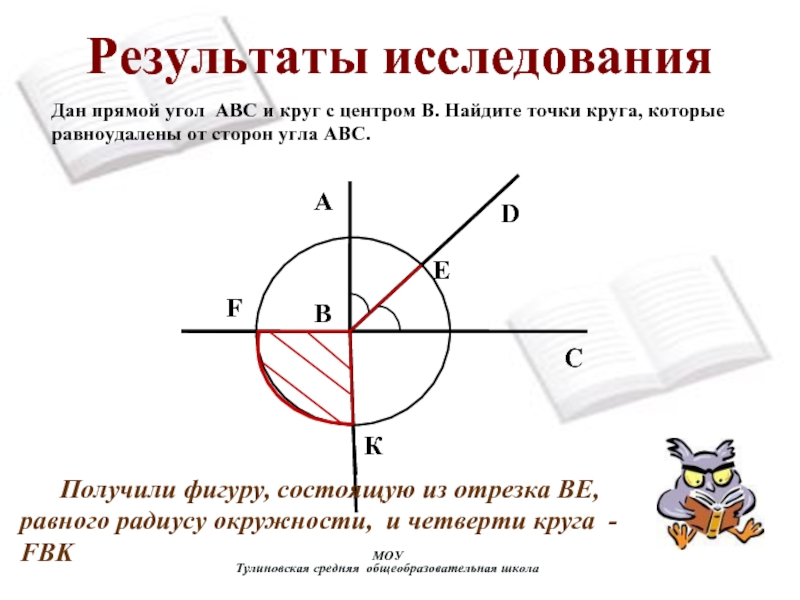
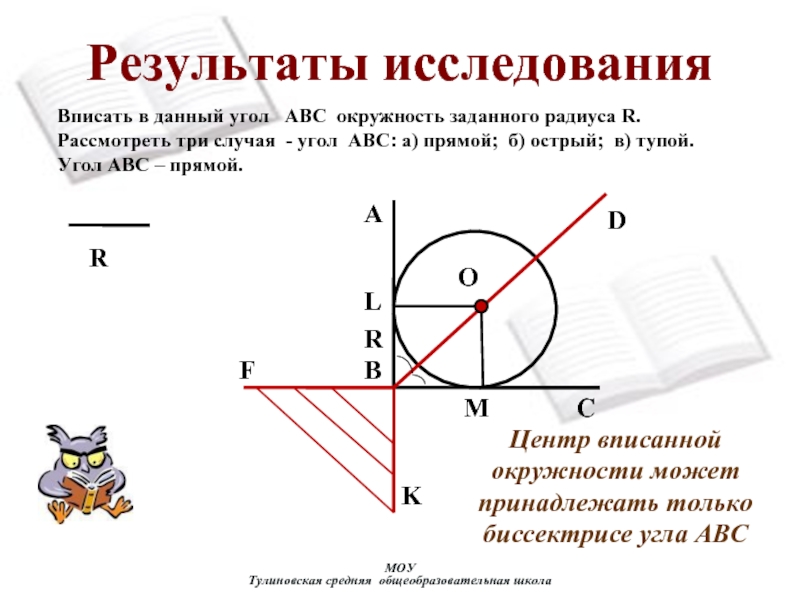
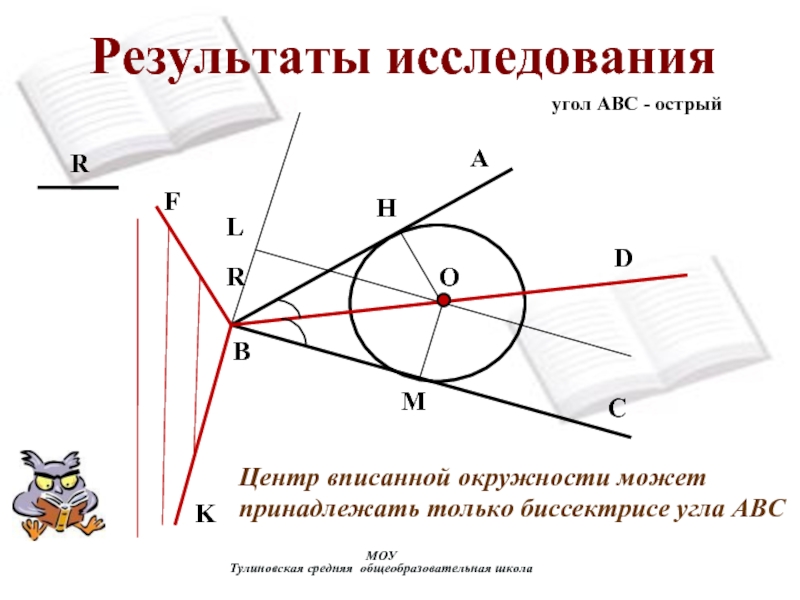
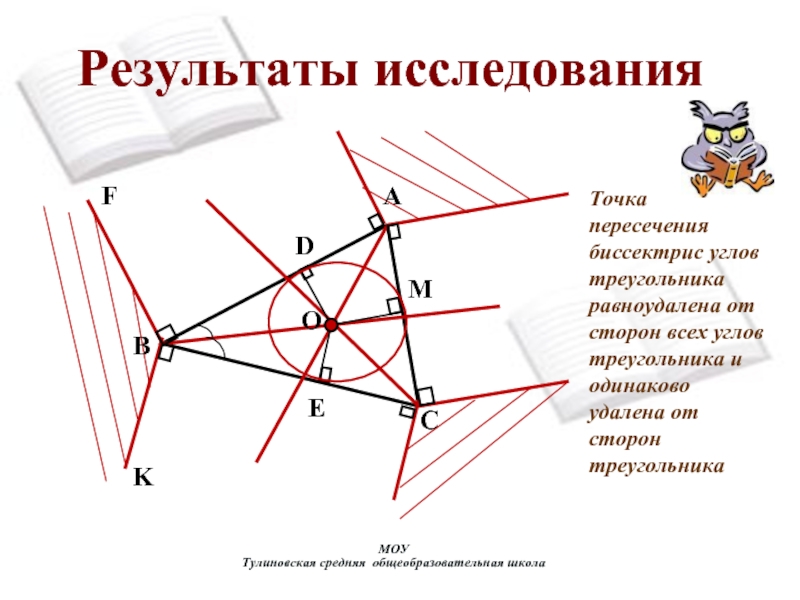
их пополам
МОУ
Тулиновская средняя общеобразовательная школа
Работу выполнила ученица 8-го класса
Лёвина ДарьяБиссектриса:
знакомая и не очень