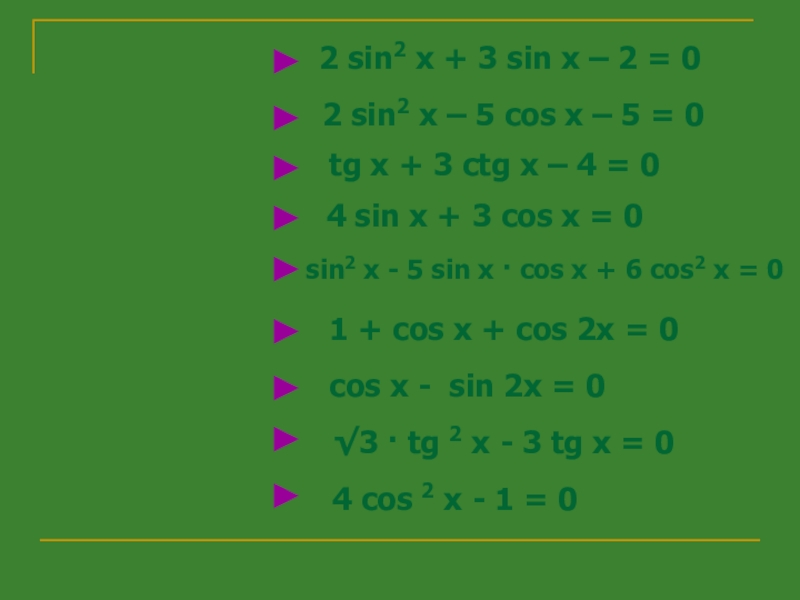Практикум по решению тригонометрических уравнений.

е б р а 1 к у р с

0
2 sin2 x – 5 cos x – 5 =

tg x + 3 ctg x – 4 = 0

sin2 x - 5 sin x · cos x + 6 cos2 x = 0

4 sin x + 3 cos x = 0

1 + cos x + cos 2x = 0

cos x - sin 2x = 0

√3 · tg 2 x - 3 tg x = 0

►

►

►

►

►

►

►

►

4 cos 2 x - 1 = 0

►

0
a · x 2 + b· x + c =

?

Уравнение 2 sin2 x + 3 sin x – 2 = 0 квадратное относительно “sin x”

0
Пусть sin x = t


2 t 2 + 3 t

D = b 2 – 4ac

D = 3 2 – 4·2·(-2) = 25

t1,2 = (-b ±√D)/2a

a

b

c

t1,2 = (-3±√25)/4

t1 = -2

t2 = ½

sin x = -2

Нет корней

sin x = ½

x=(-1)k·π/6+πk

sin x = a (lal≤1)

x=(-1)k·arcsina+πk, k∈Z

Ответ:

x=(-1)k·π/6+πk, k∈Z

0

?
Если в уравнении встречаются разные тригонометрические функции,

2 sin2 x – 5 cos x – 5 = 0

Каким тригонометрическим тождеством связаны синус и косинус одного и того же аргумента?

sin2 x + cos 2 x = 1

x – 5 cos x – 5 = 0
sin2 x

sin2 x =1 - cos 2 x

2(1- cos2x) – 5 cosx – 5 = 0

2 – 2 cos2x – 5 cosx – 5 = 0

2 cos2x + 5 cosx + 3 = 0

2 t 2 + 5 t + 3 = 0

Пусть cos x = t

a

b

c

D = b 2 – 4ac

t1,2 = (-b ±√D)/2a

cos x = a (lal≤1)

при а = - 1 частный случай

D = 5 2 – 4·2·3 = 1

t1 = -3/2

t2 = - 1

cos x = - 3/2

cos x = - 1

Нет корней

x= π + 2πk

Ответ:

x= π + 2πk, k∈Z

их заменить на какую-нибудь одну, используя тригонометрические тождества.
Каким тригонометрическим тождеством

tg x · ctg x = 1

tg x + 3 ctg x – 4 = 0

x · ctg x = 1

ctg x = 1 /

tg x + 3 · 1/tg x – 4 = 0

Пусть tg x = t

t + 3/t – 4 = 0 l · t

t 2 + 3 – 4 t = 0

t 2 – 4 t +3 = 0

a

b

c

D = (-4) 2 – 4·1·3 = 4

t1 = 1

t2 = 3

tg x = 1

tg x = 3

D = b 2 – 4ac

t1,2 = (-b ±√D)/2a

tg x = a (a-любое число)

x=arctg a+πk, k∈Z

x=π/4+πn

x=arctg3+πk

Ответ:

x=π/4+πn; x=arctg3+πk; k,n ∈ Z

косинуса, то есть на

Уравнение, в котором каждое слагаемое имеет одну и ту же степень называется однородным

4 sin x + 3 cos x = 0

Это уравнение однородное 1 - ой степени относительно sin x и cos x

A tg x + B = 0

cos x ≠ 0

4 tg x + 3 = 0

4 tg x = - 3

a x + b = 0
a x = - b
x = -b / a

tg x = a (a-любое число)

x=arctg a+πk, k∈Z

Ответ:

x=arctg(- ¾)+πk; k ∈ Z

4 sin x / cos x + 3 cos x / cos x = 0

x=arctg(-3 / 4)+πk

tg x = sinx/cosx

tg x = - 3 / 4

косинуса, то есть на

Уравнение, в котором каждое слагаемое имеет одну и ту же степень называется однородным

sin2 x - 5 sin x · cos x + 6 cos2 x = 0

Это уравнение однородное 2 - ой степени относительно sin x и cos x

A tg2 x + B tg x + C= 0

6 cos2 x = 0
l : cos 2 x ≠

Пусть tg x = t

tg2x – 5 tgx + 6 = 0

t 2 – 5t + 6 = 0

a

b

c

D = (-5) 2 – 4·1·6 = 1

t1 = 2

t2 = 3

tg x = 2

tg x = 3

D = b 2 – 4ac

t1,2 = (-b ±√D)/2a

tg x = a (a-любое число)

x=arctg a+πk, k∈Z

x=arctg3+πn

Ответ:

x=arctg2+πk; x=arctg3+πn; k,n ∈ Z

sin2 x/cos2x – (5 sin x · cos x)/cos2x + 6 cos2 x/cos2x = 0

x=arctg2+πk

tg x = sinx/cosx

решается c помощью одной из формул тригонометрии:
cos 2x

В некоторых тригонометрических уравнениях предварительно требуется преобразовать выражение с помощью формул тригонометрии:
основных тригонометрических тождеств,
сложения,
двойного аргумента

В результате получается уравнение с одной функцией одного и того же аргумента

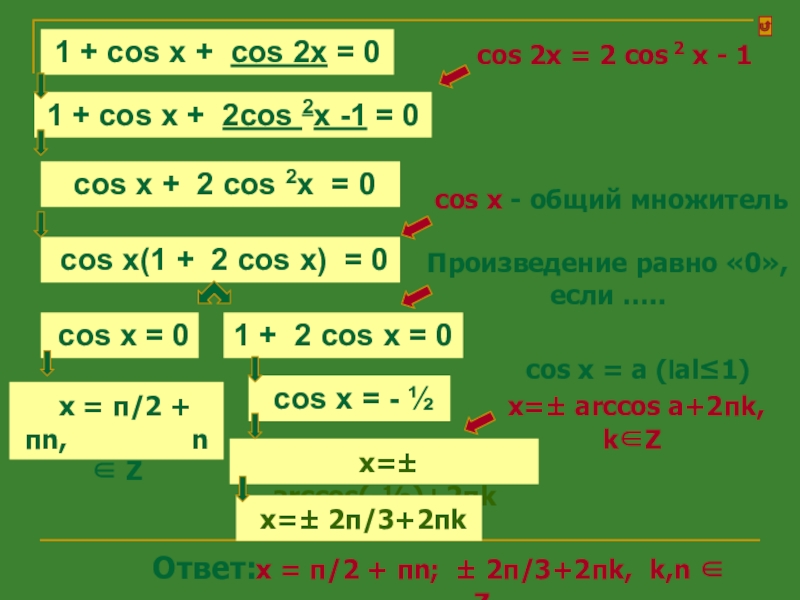
1 + cos x + cos 2x =

cos 2x = 2 cos 2 x - 1

1 + cos x + 2cos 2x -1 = 0

cos x + 2 cos 2x = 0

cos x(1 + 2 cos x) = 0

cos x - общий множитель

Произведение равно «0», если …..

cos x = 0

1 + 2 cos x = 0

cos x = - ½

x = π/2 + πn, n ∈ Z

cos x = a (lal≤1)

x=± arccos a+2πk, k∈Z

x=± 2π/3+2πk

Ответ:

x = π/2 + πn; ± 2π/3+2πk, k,n ∈ Z

c помощью формулы тригонометрии:
sin 2x = 2 sin

В некоторых тригонометрических уравнениях предварительно требуется преобразовать выражение с помощью формул тригонометрии:
основных тригонометрических тождеств,
сложения,
двойного аргумента

В результате получается уравнение, которое решается путём вынесения общего множителя за скобки

cos x - 2 sin x · cos

cos x(1 - 2 sin x) = 0

cos x - общий множитель

Произведение равно «0», если …..

cos x = 0

1 - 2 sin x = 0

sin x = ½

x = π/2 + πn, n ∈ Z

Ответ:

x = π/2 + πn; (-1)k ·π/6+πk, k,n ∈ Z

cos x - sin 2x = 0

sin 2x = 2 sin x· cos x

sin x = a (lal≤1)

x=(-1)k·arcsina+πk, k∈Z

x=(-1)k·π/6 + πk

разность

√3 · tg 2 x - 3 tg x = 0

tg x (√3 · tg x –

tg x - общий множитель

Произведение равно «0», если …..

tg x = 0

x = πn, n ∈ Z

Ответ:

x = πn; π/3+πk, k,n ∈ Z

x=π /3 + πk

√3 · tg 2 x - 3 tg x = 0

√3 · tg x – 3 = 0

tg x = 3/√3

tg x = a (a-любое число)

x=arctg a+πk, k∈Z

tg x = √3

x=arctg 0+πk

путём разложения выражения на множители

В результате выражение в левой части

(2cos x – 1)(2cos x

Произведение равно «0», если …..

2cos x – 1 = 0

х= ± arccos1/2 +2πn

Ответ:

x = ± π /3 + 2πn; ± 2 π /3 + 2πk , k,n ∈ Z

x= ± π /3 + 2πn

4 cos2 x - 1 = 0

2cos x + 1 = 0

cos x = - 1/2

cos x = a
(a-любое число)

x= ± arccos a+2πk, k∈Z

cos x = 1/2

x= ± 2 π /3 + 2πk