Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Правильные многогранники.
Содержание
- 1. Правильные многогранники.
- 2. Правильные многогранникиМногогранник называется правильным, если все его
- 3. Названия многогранников пришли из Древней Греции, в
- 4. Додекаэдр Существует правильный многогранник, у которого все
- 5. Свойства Все двадцать вершин додекаэдра лежат по
- 6. Основные формулы Если за длину ребра
- 7. Слайд 7
- 8. Скачать презентанцию
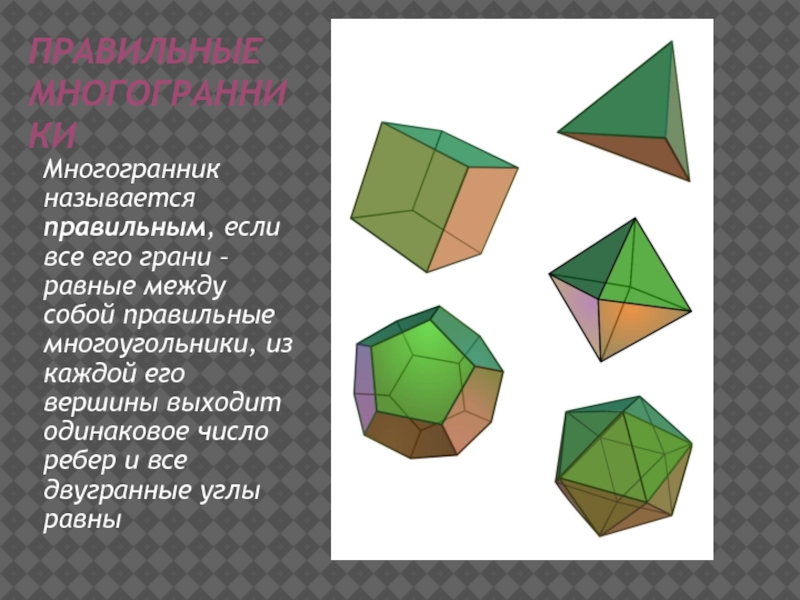
Правильные многогранникиМногогранник называется правильным, если все его грани – равные между собой правильные многоугольники, из каждой его вершины выходит одинаковое число ребер и все двугранные углы равны
Слайды и текст этой презентации
Слайд 3Названия многогранников
пришли из Древней Греции,
в них указывается число
граней:
«эдра» грань;
«тетра» 4;
«гекса» 6;
«окта»
8;«икоса» 20;
«додека» 12.
Слайд 4Додекаэдр
Существует правильный многогранник, у которого все грани правильные пятиугольники
и из каждой вершины выходит 3 ребра. Этот многогранник имеет
12 граней, 30 ребер и 20 вершин и называется додекаэдром (dodeka – двенадцать).Сумма плоских углов при каждой вершине равна 324 градуса
Слайд 5Свойства
Все двадцать вершин додекаэдра лежат по пять в четырёх параллельных плоскостях,
образуя в каждой из них правильный пятиугольник.
Двугранный угол между любыми двумя
смежными гранями додекаэдра равен arccos(-1/√5)≈116°,565.Сумма плоских углов при каждой из 20 вершин равна 324°, телесный(трёхгранный) угол равен arccos(-11/5√5)≈2,9617 стерадиан.
В додекаэдр можно вписать куб так, что стороны куба будут диагоналями додекаэдра.
Додекаэдр имеет три звёздчатые формы.
В додекаэдр можно вписать пять кубов. Если заменить пятиугольные грани додекаэдра плоскими пятиугольными звездами так, что исчезнут все ребра додекаэдра, то получим пространство пяти пересекающихся кубов. Додекаэдр как таковой исчезнет. Вместо замкнутого многогранника появится открытая геометрическая система пяти ортогональностей. Или симметричное пересечение пяти трехмерных пространств.
Слайд 6Основные формулы
Если за длину ребра принять, то площадь поверхности
додекаэдра:
Объём додекаэдра:
Радиус описанной сферы:
Радиус вписанной сферы:
