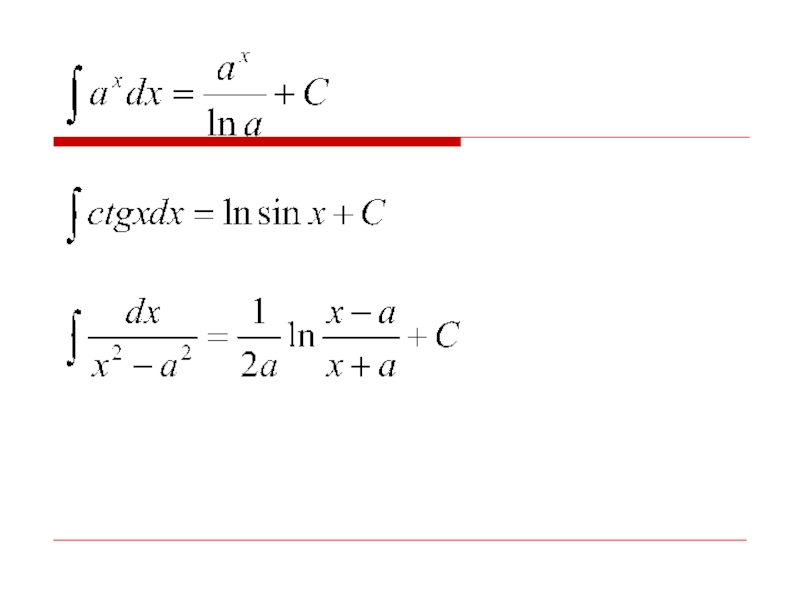Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация десятичный и натуральный логарифмы
Содержание
- 1. Презентация десятичный и натуральный логарифмы
- 2. ЦельЗнать формулы производной показательной функции, производной функцииУметь
- 3. Натуральные логарифмы:
- 4. Дифференцирование функции Например,
- 5. Дифференцирование функции
- 6. Основные формулы
- 7. Слайд 7
- 8. Вычислить значение производной функции
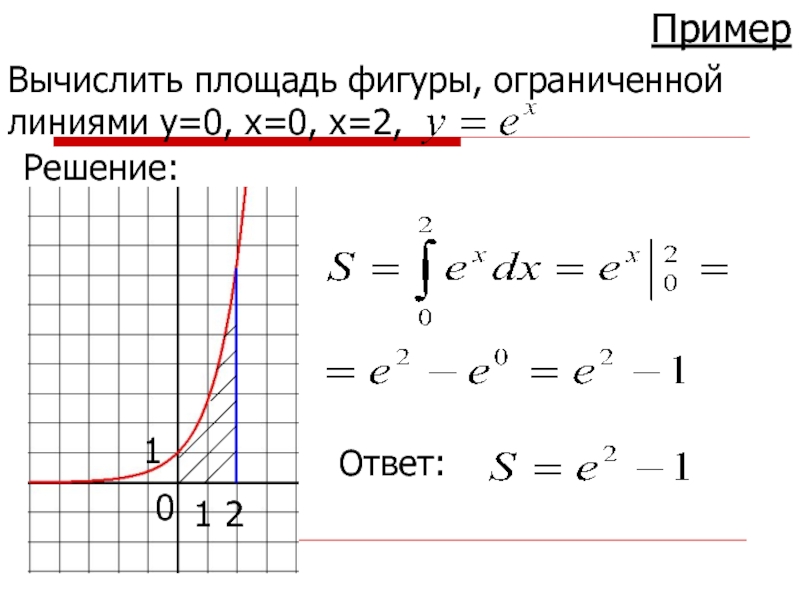
- 9. ПримерВычислить площадь фигуры, ограниченной линиями y=0, x=0, x=2, Решение:2110Ответ:
- 10. Пример Исследовать на экстремум и схематически изобразить график функцииРешение:1)2)
- 11. 3)-2x0++-4)x=-2 – точка максимумаx=0 – точка минимума
- 12. Подготовка к ЕНТ1.Найдите у′ (х) если у(х)
- 13. 3.Найдите у′ (х), если у(х) = log5х
- 14. 5.Найдите производную функции f(х)= 3х^2+2х( lnх +х^2)
- 15. 6.Найдите u′ (х), если u(х) =
- 16. Домашнее заданиеУровень – АНайдите производную функции
- 17. Скачать презентанцию
ЦельЗнать формулы производной показательной функции, производной функцииУметь решать задачи, с использованием производной показательной функции и функции Знать определение первообразной, правила нахождения первообразных, формулу для вычисления интеграла Знать формулы первообразной логарифмической функции
Слайды и текст этой презентации
Слайд 1Дифференцирование показательной и логарифмической функций
Подготовил учитель математики СШ №12
Пышкин К.А
Слайд 2Цель
Знать формулы производной показательной функции, производной функции
Уметь решать задачи, с
использованием производной показательной функции и функции
Знать определение первообразной, правила
нахождения первообразных, формулу для вычисления интеграла Знать формулы первообразной логарифмической функции и натурального логарифма
Уметь находить первообразные различных логарифмических функций
Слайд 12Подготовка к ЕНТ
1.Найдите у′ (х) если у(х) =
A) 5х −
B)
5х +
5х – 5lnх
5х ∙ln5−5
D) 5х ∙ln5−
E) 5х ∙
ln5+2.Дана функция у(х)= 2е^х –log2х.
Найдите у′ (х)
A) 2ех −
B) 2ех +
C) 2ех −
D) 2ех +
E) ех -
Слайд 133.Найдите у′ (х), если у(х) = log5х +5х
A)
В)
С)
D)
E)
+5х∙ln5
+5х
+ 5х ∙ln5
+ ln5
4.Найдите h′ (х), если h(х)
= =х^3+х^2 ∙lnх3х^2+2х
B) 3х^2+2х +х∙ lnх
3х^2+2х∙ lnх +х
х^3+2х∙ lnх+х^2
3х^2+2х∙ lnх +х^2
Слайд 16Домашнее задание
Уровень – А
Найдите производную функции
Уровень – В
Найдите наибольшее значение функции
на
отрезке Уровень –С
Через точку графика функции у = ех –
с абсциссой х0 = 1 проведена касательная.
Найдите тангенс угла наклона этой касательной к оси абсцисс.
