Презентация для работы по подготовке к ЕГЭ по математике по теме "Решение С2 ВКМ"

Обязательное знание правил и формул.
Постоянное совершенствование учебных навыков на

практике.
Проверка знаний и умений учащихся.

измерений – здесь указана рекомендуемая литература по отдельным предметам
www.ege.edu.ru –

портал поддержки ЕГЭ, где размещена вся основная информация о ЕГЭ
www.mioo.ru – сайт Московского института открытого образования, где действует система прямых ссылок на наиболее важные страницы портала поддержки

Информационная поддержка участника ЕГЭ

ученику;
- рекомендации родителям;
2. систематическая связь с родителями.

и при систематической подготовке к ним.
Необходимо внимательно выслушивать теоретический материал

на уроках.
Старайтесь не пропускать без уважительной причины уроки математики.
Не допускайте формального усвоения программного материала.
Помните, что умение решать задачи является следствием глубоко понятого соответствующего теоретического материала.
Выполняйте все домашние задания самостоятельно, и своевременно выясняйте непонятные моменты.
Составьте свой личный план подготовки к экзамену. Покажите его учителю или другому квалифицированному специалисту для подтверждения его правильности и соответствия вашим индивидуальным способностям.
Регулярно занимайтесь дополнительно по личному плану, не реже 1 раза в неделю.
Запомните: вся подготовка к экзамену зависит лично от каждого из вас.
Роль учителя в школе действительно велика, но он не всемогущ, и обучить может лишь того, кто хочет учиться и кто сам учится.

если у Вас нет математического образования, то Вы ничем не

можете помочь своему ребенку при подготовке к ЕГЭ.
Это всегда можно сделать, организуя и контролируя его самоподготовку. Здесь Ваша помощь просто необходима.
Ознакомьтесь с « Рекомендациями ученику» и помогайте ребенку их выполнять.
Контролируйте его работу и посещаемость на уроках математики в школе (не реже 1 раза в месяц встречайтесь с учителем математики и старайтесь выполнять его рекомендации).
Организуйте качественное питание и отдых ребенка в течение всего учебного года (особенно в период сдачи экзаменов).

понятной форме.
Формы работы на уроках необходимо разнообразить, повышая

тем самым интерес к предмету.
Необходимо добиваться от учащихся не формального усвоения программного материала, а глубокого осознанного его понимания.
В процессе преподавания необходимо делать определенные акценты на те разделы, которые представлены в тестах ЕГЭ.
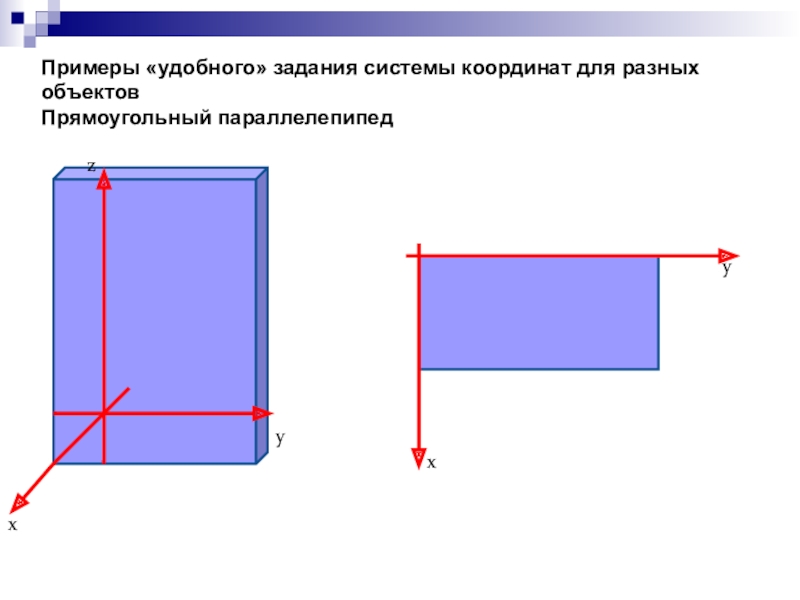
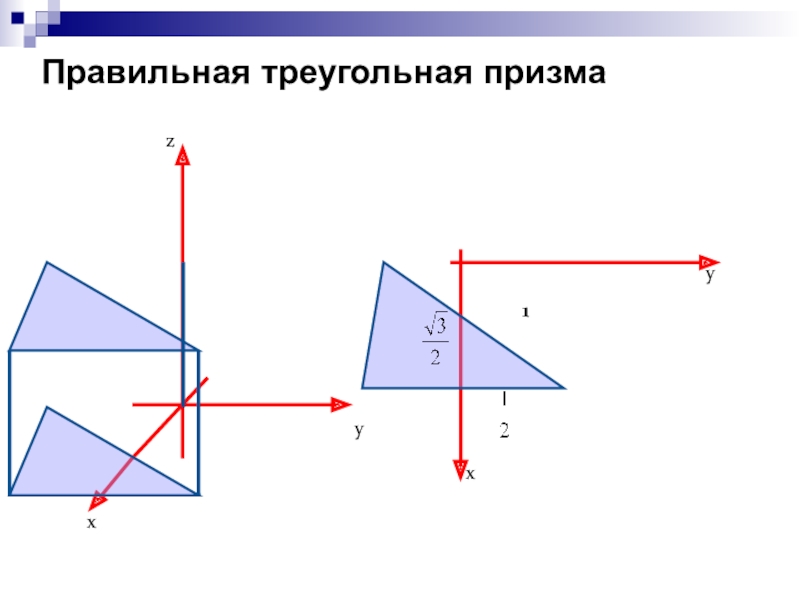
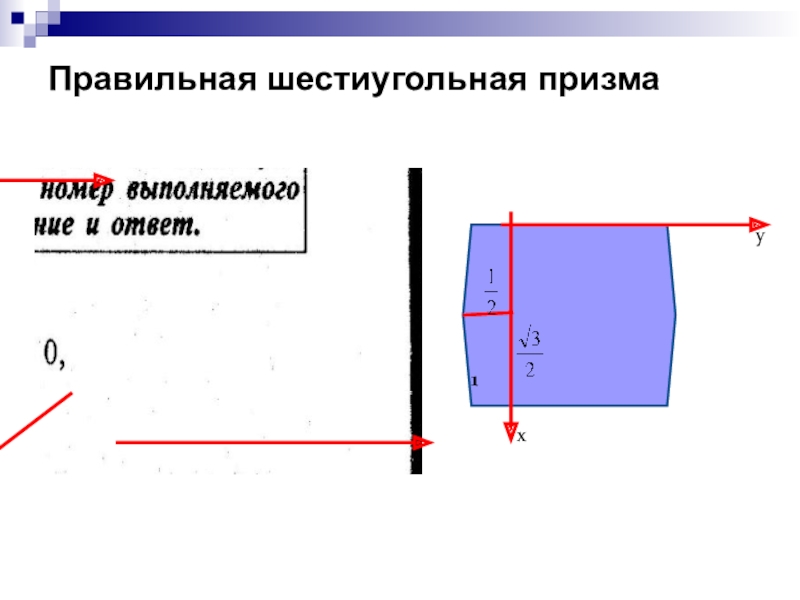
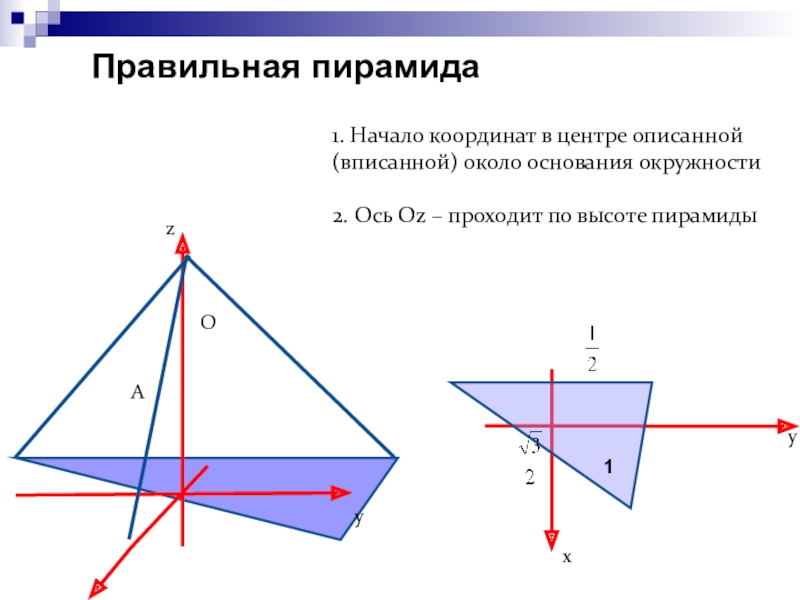
Объяснение нового материала необходимо строить как можно более наглядно, создавать яркие образы.
Необходимо разработать систему контроля знаний учеников и возможность устранения пробелов в их знаниях.
Необходимо сформировать у всех учащихся достаточно высокий уровень учебной самостоятельной деятельности,

Рекомендации учителю

не единственный метод решения задач С2
Метод координат универсален, потому что

есть алгоритм решения для любого типа заданий С2.
Целесообразно задавать систему координат специальным способом для разных объектов.
Целесообразно изображать плоскость Оху и основание геометрического тела в ней отдельно.

Ось Оz – проходит по высоте пирамиды

А
О




1

ребра которой раны 1, найдите косинус угла между прямыми АВ1

и ВС1

1

1/2

плоскостью BDD1.

А
D
С
В

найдите косинус двугранного угла, образованного гранями
SBC и SCD.
Введем прямоугольную

систему координат (см.рис.)
Найдем угол между перпендикулярами к плоскостям SBC и SCD. Обозначим искомый угол α.
Составим уравнения плоскостей.

О

плоскости SBC,
то их координаты удовлетворяют уравнению (1)
Составим и решим

систему уравнений

Неизвестных 4, уравнений 3
Пусть d=1

а боковые ребра равны 2, найдите расстояние от точки F

до
Прямой BG, где G – середина ребра SC

плоскости ВDA1
Решение:
Введем прямоугольную систему координат

а боковые ребра равны 2, найдите расстояние от точки А

до
плоскости SBC.

O

NM- общий перпендикуляр прямых АD1 и A1C1

между направляющими векторами, то косинус угла между АЕ и ВК

равен