Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
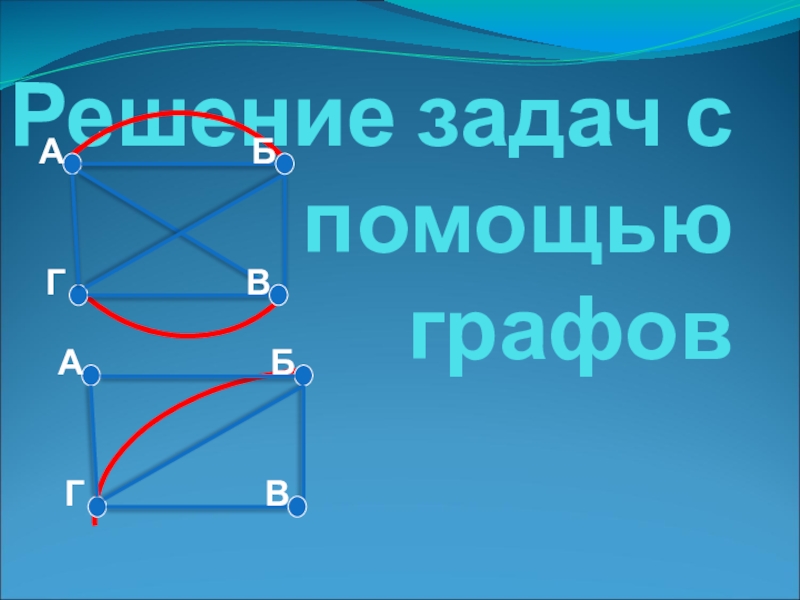
Презентация для урока "Решение задач с помощью графов"
Содержание
- 1. Презентация для урока "Решение задач с помощью графов"
- 2. Жизнь украшается двумя вещами: занятием математикой и ее преподаванием" Пуассон С.П.
- 3. Проверка домашней работы
- 4. „Счет и вычисления — основа порядка в
- 5. Счётчик4)Какой будет остаток от деления произведения 67*669*6668
- 6. „У математиков существует свой язык —
- 7. Идет крестьянин и плачется: „Эхма! Жизнь моя
- 8. Повторим…ГрафПростейшая модель системы. Отображает элементарный состав системы
- 9. ПовторимЕсли все вершины графа четны то граф
- 10. Первый тип задач «Кто играет Ляпкина-Тяпкина?» В
- 11. Второй тип задачЗаданный плоский граф требуется вычертить,
- 12. Задача 1Некто давал 1000000 рублей каждому, кто
- 13. Задача 2 Магомет вместо подписи (он был
- 14. Задача 3Можно ли вычертить одним росчерком фигуру, показанную на рисунке?
- 15. Задача 4Муха забралась в банку из-под сахара
- 16. „Математику нельзя изучать, наблюдая как это делает
- 17. «В задачах, которые ставит перед нами жизнь, экзаменатором является сама природа.»
- 18. Леонард Эйлер Одним из крупнейших математиков
- 19. Гена
- 20. Решение домашней задачи5∙ 0,35 = 1,75 литров
- 21. Скачать презентанцию
Слайды и текст этой презентации
Слайд 4„Счет и вычисления — основа порядка в голове„
Песталоцци
Игра «Счетчик»
1) Физик, устав, лег спать в 10 часов вечера; предварительно завел будильник на 12 часов следующего дня. Сколько часов он успел проспать, прежде чем будильник его разбудит?
2) Сколько месяцев в году содержат по 30 дней?
3) Вот вам 3 пилюли - сказал доктор. Принимайте по 1 через каждые полчаса. На сколько вам хватит прописанных доктором пилюль?
Слайд 5Счётчик
4)Какой будет остаток от деления произведения 67*669*6668 на 6
5)
Найди остаток от деления на 5 следующей суммы (7+56+558+5558)/5
6)
Решить уравнение: (((х+2)/4)-2)*6=12 7) Найди число, если 3% от него 240
8) 17% от 50
9) 3000% от 50
10) Найди процентное отношение чисел 48 к 16
11) Вычислите 0.1% от 700
Слайд 7Идет крестьянин и плачется: „Эхма! Жизнь моя горькая! Заела нужда
совсем! Вот в кармане только несколько грошей медных Болтается, да
и те сейчас нужно отдать. И как это у других бывает, что на всякие деньги они еще деньги получают? Право, хоть бы кто помочь мне захотел„.Только успел это сказать, как глядь, а перед ним черт стоит.
-Что ж, - говорит, - если хочешь, я тебе помогу. И это совсем нетрудно. Вот видишь этот мост через реку?
-Вижу! — говорит крестьянин, а сам заробел.
-Ну, так стоит тебе перейти только через мост — у тебя будет вдвое больше денег, чем есть. Перейдешь назад, опять станет вдвое больше, чем было. И каждый раз, как ты будешь переходить мост, у тебя будет вдвое больше денег, чем было до этого перехода.
-Ой ли? — говорит крестьянин.
-Верное слово! — уверяет черт. — Только, чур, уговор! За то, что я тебе удваиваю деньги, ты каждый раз, перейдя через мост, отдавай мне по 24 копейки. Иначе не согласен.
-Ну, что же, это не беда! — говорит крестьянин. — Раз деньги все будут удваиваться, так отчего же 24 копейки тебе каждый раз не отдать?
Ну ка, попробуем!
Перешел он через мост один раз, посчитал деньги. Действительно, стало вдвое больше. Бросил он 24 копейки черту и перешел второй раз. Опять денег стало вдвое больше, чем перед этим. Отсчитал он 24 копейки, отдал черту и перешел через мост в третий раз. Денег стало снова вдвое больше. Но только и оказалось их ровнехонько 24 копейки, которые по уговору о должен был отдать черту. Отдал он их и остался без копейки.
Сколько же у крестьянина было денег сначала?
Слайд 8Повторим…
Граф
Простейшая модель системы. Отображает элементарный состав системы и структуру связей
Сеть
Граф
с возможностью множества различных путей перемещения по ребрам между некоторыми
парами вершин
Ребро соединяет две вершины графа
элемент (точка) графа, обозначающий объект любой природы, входящий в множество объектов, описываемое графом
Вершина
Ребро
это ориентированное ребро.
Дуга
ребро, начало и конец которого находятся в одной и той же вершине
Петля
Слайд 9Повторим
Если все вершины графа четны то граф можно обойти за
один цикл, не проходя ни одного ребра дважды.
Если 2
вершины графа нечетные, то замкнутого цикла не существует, но можно выйдя из одной нечетной вершины обойти весь граф и вернуться во вторую нечетную вершину.
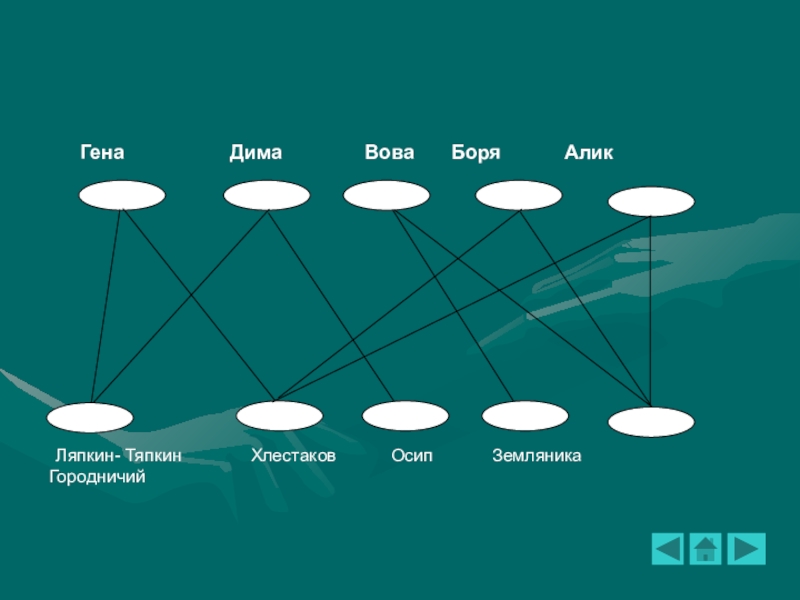
Слайд 10Первый тип задач
«Кто играет Ляпкина-Тяпкина?»
В школьном драмкружке решили
ставить гоголевского «Ревизора». И тут разгорелся жаркий спор. Всё началось
с Ляпкина-Тяпкина. — Ляпкин-Тяпкин буду я! - решительно заявил Гена.— Нет, я буду Ляпкиным-Тяпкиным, - возразил Дима.
— С раннего детства мечтал воплотить этот образ на сцене.
— Ну, хорошо, согласен уступить роль, если мне дадут сыграть Хлестакова,- проявил великодушие Гена.
— ...А мне — Осипа, - не уступил ему в великодушии Дима.
— Хочу быть Земляникой или Городничим, - сказал Вова.
— Нет, городничим буду я, - хором закричали Алик и Боря. — Или Хлестаковым, - добавили они одновременно.
Удастся ли распределить роли так, чтобы исполнители были довольны? (Мы не спрашиваем, будут ли довольны зрители.)
Слайд 11Второй тип задач
Заданный плоский граф требуется вычертить, не отрывая карандаша
от бумаги и не обводя дважды один и тот же
участок графа. Если при этом получается замкнутая линия, начинающаяся и кончающаяся в одной и той же вершине, то такой граф называют Эйлеровым
Слайд 12Задача 1
Некто давал 1000000 рублей каждому, кто начертит следующую фигуру.
Требование: одним непрерывным росчерком т. е. не отнимая пера или
карандаша от бумаги и не удваивая ни одной линии
Слайд 13Задача 2
Магомет вместо подписи (он был неграмотен) описывал одним
росчерком состоящий из двух рогов Луны знак, представленный на рисунке.
Как он это делал, подумай, пронумеруй точки.
Слайд 15Задача 4
Муха забралась в банку из-под сахара . Банка имеет
форму куба. Сможет ли муха последовательно обойти все 12 рёбер
куба, не проходя дважды по одному ребру, подпрыгивать и перелетать с места на места на место не разрешается ?
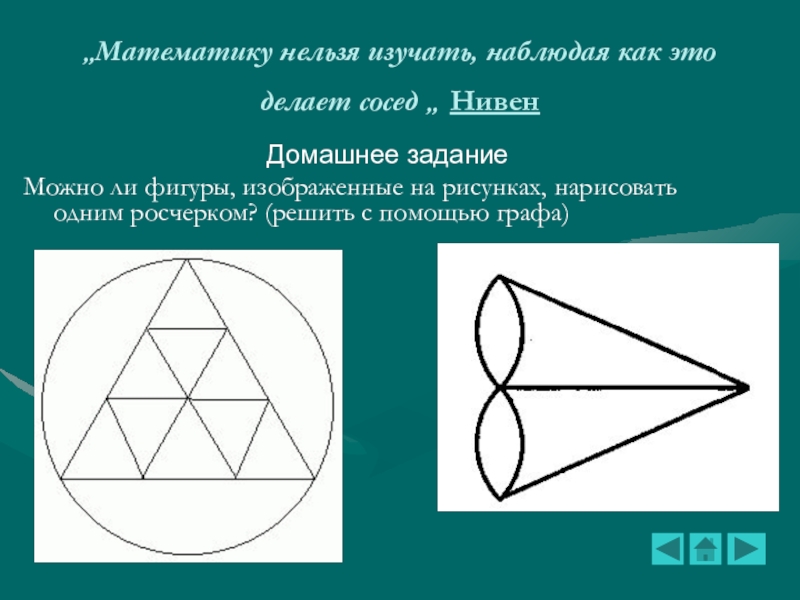
Слайд 16„Математику нельзя изучать, наблюдая как это делает сосед „ Нивен
Домашнее
задание
Можно ли фигуры, изображенные на рисунках, нарисовать одним росчерком?
(решить с помощью графа)
Слайд 18Леонард Эйлер
Одним из крупнейших математиков XVIII века был
Леонард Эйлер. Он родился в швейцарском городе Базеле, где в
15 лет закончил университет, а в 17 лет получил степень магистра. Во время обучения в университете Эйлер брал уроки у одного из самых известных математиков того времени Иоганна Бернулли. Нет такой области математики, где Эйлер не сказал своего слова. Работал он сутками напролет в любой обстановке, опубликовал примерно 850 работ. Он легко обнаруживал новые задачи и методы их решения.
Слайд 20Решение домашней задачи
5∙ 0,35 = 1,75 литров жира в 5
литрах сливок
4∙ 0,20 = 0,8 литров жира в 4
литрах 1,75 + 0,8 = 2,55 литров жира в смеси
5 + 4+1 = 10 литров смесь
5. 2,55: 10 = 0,255 литров = 25,5% жирность смеси