Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Ох уж, эта тригонометрия!
Содержание
- 1. Ох уж, эта тригонометрия!
- 2. “Дороги не те знания, которые отлагаются в
- 3. “ Математику уже затем учить надо, что она ум в порядок приводит ”М.В.Ломоносов
- 4. Обобщающий урок по теме: «Общие методы решения тригонометрических уравнений»
- 5. «Не бойтесь формул! Учитесь владеть этим инструментом
- 6. Единичная окружность разделена на 24 равные части.
- 7. Слайд 7
- 8. Слайд 8
- 9. Слайд 9
- 10. Является ли число π корнем уравнения?
- 11. 1.Простешие тргонометрические уравнения2.Уравнения ,решаемые введением замены3.Уравнения ,приводимые
- 12. 1) 2sinx cos 5x – cos 5x
- 13. Решите уравнение соs2x=sin(x+π/2).б) Найдите корни этого уравнения, принадлежащие промежутку [-2π; -π]
- 14. Это интересно
- 15. История тригонометрии По звездам вычисляли местонахождение
- 16. Математический маятникНа рисунке изображены колебания маятника, он движется по кривой, называемой косинусом.
- 17. Описание движения рыб в воде тригонометрическими функциями
- 18. мост
- 19. Детская школа Гауди в Барселоне, испания
- 20. ЗаключениеОказывается, что тригонометрия была вызвана к жизни
- 21. Скачать презентанцию
“Дороги не те знания, которые отлагаются в мозгу, как жир; дороги те, которые превращаются в умственные мышцы” Г. Спесер
Слайды и текст этой презентации
Слайд 2“Дороги не те знания, которые отлагаются в мозгу, как жир;
дороги те, которые превращаются в умственные мышцы”
Слайд 5«Не бойтесь формул! Учитесь владеть этим инструментом Человеческого гения! В
формулах заключено величие и могущество разума…»
А. А. Марков
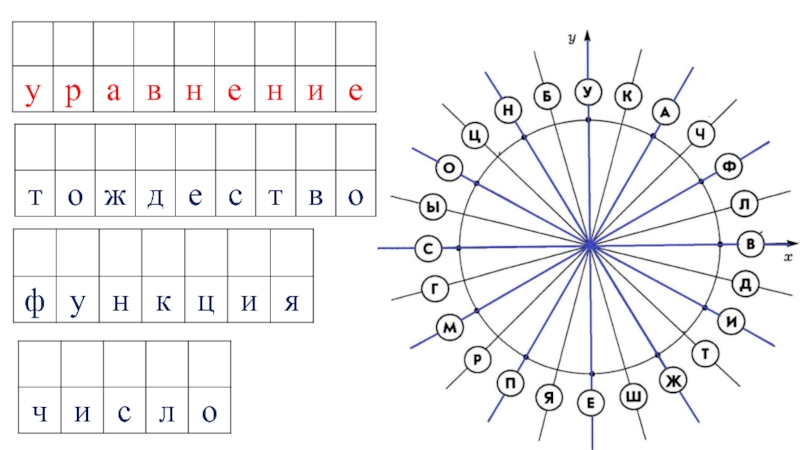
Слайд 6Единичная окружность разделена на 24 равные части. Найдите точки, соответствующие
результатам поворота начальной точки В на указанные в таблице углы.
Слайд 111.Простешие тргонометрические уравнения
2.Уравнения ,решаемые введением замены
3.Уравнения ,приводимые к линейным и
квадратным
4.Однородные тригонометрические уравнения
5.Уравнения ,решаемые введением вспомогательного угла
6.Метод преобразования суммы в
произведение7.Метод преобразования произведения в
сумму
Слайд 121) 2sinx cos 5x – cos 5x =0;
2) sin (π+x)=0
3)3tg 2 x + 2tg x -1=0
4) 2 cos2 x + 9cos x +14=0;
5) sin 2х = -1
6)2sinx – 3cosx = 0
7) cos 3x = 0;
8) cos (х – π/4) = ½;
9) sin (x/2+ π /3)= -1/2.
10) 3sin2x – 4sinx cosx + cos2x = 0
11)√3tg2x + 1 = 0
12) 3cos2x – sinx – 1 =0
13) 2cos(π/3 + 3x) – √3 = 0
Слайд 13 Решите уравнение соs2x=sin(x+π/2).
б) Найдите корни этого уравнения, принадлежащие промежутку
[-2π; -π]
Слайд 15История тригонометрии
По звездам вычисляли местонахождение корабля в море.
Древние люди вычисляли высоту дерева, сравнивая длину его тени с
длиной тени от шеста, высота которого была известна. Тригонометрия (от греч. trigwnon - треугольник и metrew - измеряю)
Слайд 16Математический маятник
На рисунке изображены колебания маятника, он движется по кривой,
называемой косинусом.
Слайд 17Описание движения рыб в воде тригонометрическими функциями
Движение рыб
в воде происходит по закону синуса или косинуса, если зафиксировать
точку на хвосте, а потом рассмотреть траекторию движения.При плавании тело рыбы принимает форму кривой, которая напоминает график функции y=tgx.
Слайд 20Заключение
Оказывается, что тригонометрия была вызвана к жизни необходимостью производить измерения
углов, но со временем развилась и в науку о тригонометрических
функциях.Оказывается, что тригонометрия тесно связана с физикой, встречается в природе, музыке, архитектуре и медицине.
Следовательно, тригонометрия нашла отражение в нашей жизни, и сферы, в которых она играет важную роль, будут расширяться.











![Ох уж, эта тригонометрия! Решите уравнение соs2x=sin(x+π/2).б) Найдите корни этого уравнения, принадлежащие промежутку [-2π; -π] Решите уравнение соs2x=sin(x+π/2).б) Найдите корни этого уравнения, принадлежащие промежутку [-2π; -π]](/img/thumbs/13d08259fd20d6ffdeac273059d4a054-800x.jpg)