Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация по математике "Пифагор и его теорема"
Содержание
- 1. Презентация по математике "Пифагор и его теорема"
- 2. Дошедшие до нас биографические сведения о Пифагоре
- 3. .Родителями Пифагора были Мнесарх и Партенида с
- 4. Достоверно известно, что Пифагор посещал Египет и
- 5. Ему было лет тридцать, когда он приехал
- 6. Вернувшись на Самос, Пифагор нашел родину в
- 7. Сюда, в богатый торговый порт у берегов
- 8. ...Прошло 20 лет. Слава о братстве разнеслась
- 9. Геометрия владеет двумя сокровищами: одно из них
- 10. Доказательство теоремы считалось в кругах учащихся средних
- 11. Самое простое доказательствоРассмотрим квадрат, показанный на рисунке.
- 12. Доказательство Евклида Дано: ABC-прямоугольный треугольник Доказать:SABDE=SACFG+SBCHIДОКАЗАТЕЛЬСТВО:Пусть ABDE-квадрат,
- 13. Отсюда и из равенства треугольников ACE и
- 14. Алгебраическое доказательствоДано: ABC-прямоугольный треугольникДоказать: AB2=AC2+BC2 Доказательство: 1) Проведем высоту
- 15. Геометрическое доказательство Дано: ABC-прямоугольный треугольникДоказать: BC2=AB2+AC2Доказательство: 1) Построим
- 16. В Средние века был создан значок, символизирующий
- 17. Пифагоровы штаны на все стороны равныМедаль Пифагора
- 18. Слайд 18
- 19. Слайд 19
- 20. В настоящее время известно, что эта теорема
- 21. Ты же будь твёрдым: божественный род присутствует
- 22. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Пифагор и его теорема
Тазетдинова Алина, 11 класс В
МБОУ педагогический лицей
г.
Димитровграда Ульяновской области
Слайд 2Дошедшие до нас биографические сведения о Пифагоре отрывочны и далеко
не достоверны.
С его именем связано много легенд.
Пифагор Самосский (др.-греч.
Πυθαγόρας ὁ Σάμιος, лат. Pythagoras; 570—490 гг. до н. э.) — древнегреческий философ, математик и мистик, создатель религиозно-философской школы пифагорейцев.Слайд 3.
Родителями Пифагора были Мнесарх и Партенида с острова Самос. Мнесарх
был камнерезом (Диоген Лаэртский); по словам же Порфирия он был
богатым купцом из Тира, получившим самосское гражданство за раздачу хлеба в неурожайный год. Первая версия предпочтительнее, так как Павсаний приводит генеалогию Пифагора по мужской линии от Гиппаса из пелопоннесского Флиунта, бежавшего на Самос и ставшего прадедом Пифагора. Партенида, позднее переименованная мужем в Пифаиду, происходила из знатного рода Анкея, основателя греческой колонии на Самосе.Рождение ребёнка будто бы предсказала Пифия в Дельфах, потому Пифагор и получил своё имя, которое значит «тот, о ком объявила Пифия». В частности, Пифия сообщила Мнесарху, что Пифагор принесет столько пользы и добра людям, сколько не приносил и не принесет в будущем никто другой. Поэтому, на радостях, Мнесарх дал жене новое имя Пифаида и дал имя ребенку Пифагор. Пифаида сопровождала мужа в его поездках, и Пифагор родился в Сидоне Финикийском (по Ямвлиху) примерно в 570 до н. э.
Слайд 4Достоверно известно, что Пифагор посещал Египет и Вавилон. В одной
из греческих колоний Южной Италии им была основана знаменитая «Пифагорова
школа», сыгравшая важную роль в научной и политической жизни древней Греции. Именно Пифагору приписывают доказательство известной геометрической теоремы. На основе преданий, распространенных известными математиками (Прокл, Плутарх и др.), длительное время считали, что до Пифагора эта теорема не была известна, отсюда и название – теорема Пифагора. Сейчас известно, что эта теорема была известна до него, но именно Пифагор первым доказал ее.Для тогдашней греческой молодежи посещение чужих стран было главным способом расширить запас знаний, и поэтому юность свою Пифагор провел в путешествиях
Слайд 5Ему было лет тридцать, когда он приехал в Египет и
там познакомился с древней мудростью жрецов: медициной, математикой и метеорологией.
Говорят, что при вторжении персов в Египет Пифагор был захвачен в плен и отвезен в Вавилон.Существует легенда, будто в то время он встретился с иранским пророком Заратустрой и даже побывал в Индии. Но, по мнению большинства историков, эти сведения (записанные, кстати сказать, много веков спустя после смерти мудреца) являются скорее романом, чем историей . Наиболее достоверными можно признать указания на поездки Пифагора в Вавилон и особенно Египет, с которыми греки в то время имели тесные отношения. Вполне понятно, что религии этих стран должны были произвести большое впечатление на «любителя мудрости» и дать богатую пищу его воображению и мысли.
Слайд 6Вернувшись на Самос, Пифагор нашел родину в руках диктатора Поликрата,
который упрочил свою власть, опираясь на союз с персами. Поначалу
могло показаться, что остров расцвел после трудных лет политических переворотов. Поликрат, сам выходец из торговой среды, поощрял ремесла и искусства. Повсюду сооружались обширные постройки, поражавшие своим великолепием. При дворе правителя находили приют выдающиеся поэты и художники.Но Пифагор быстро понял цену этой золотой клетки. Опека властей оказалась тяжким бременем для свободы мысли. По словам Порфирия, философ «видел, что тирания слишком сильна, чтобы свободному человеку можно было доблестно переносить надзор и деспотизм» . Пифагор проникся отвращением к самосскому режиму и задумал навсегда покинуть отечество. «Ненавидя душой тиранию, сам он изгнанье избрал»,— говорил Овидий, читавший одну из древних биографий философа . О подробностях этого переселения (или изгнания ?) ничего не известно. Мы знаем лишь, что в 540 г. Пифагор сел на корабль, отплывавший в Италию, и через некоторое время прибыл в город Кротон.
Слайд 7Сюда, в богатый торговый порт у берегов Тарентского залива, в
так называемую «Великую Грецию», стремились многие путешественники, купцы и мастера.
В этом царстве колонистов общая атмосфера была намного свободнее, чем на Самосе. Пропаганда учения Пифагора обеспокоила власть имущих...После нескольких месяцев притязаний со стороны Поликрата, Пифагор переселяется в Кротон. В Кротоне Пифагор учредил нечто вроде религиозно-этического братства или тайного монашеского ордена ("пифагорейцы"), члены которого обязывались вести так называемый пифагорейский образ жизни. Это был одновременно и религиозный союз, и политический клуб, и научное общество.
Надо сказать, что некоторые из проповедуемых Пифагором принципов достойны подражания и сейчас.
Слайд 8...Прошло 20 лет. Слава о братстве разнеслась по всему миру.
Однажды к Пифагору приходит Килон, человек богатый, но злой, желая
спьяну вступить в братство. Получив отказ, Килон начинает борьбу с Пифагором, воспользовавшись поджогом его дома. При пожаре пифагорейцы спасли жизнь своему учителю ценой своей, после чего Пифагор затосковал и вскоре покончил жизнь самоубийством.Слайд 9Геометрия владеет
двумя сокровищами:
одно из них –
это теорема
Пифагора.
Иоган Кеплер Формулировки теоремы Пифагора различны. Общепринятой считается следующая:
«В прямоугольном
треугольнике квадрат
гипотенузы равен
сумме квадратов
катетов»
Во времена Пифагора формулировка теоремы звучала так:
«Квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на катетах»
Слайд 10Доказательство теоремы считалось в кругах учащихся средних веков очень трудным
«Dons
asinorum»-
«ОСЛИНЫЙ мост»
или
“elefuga” -
«бегство убогих»
а сама теорема , из-за
чертежей–«ветряной мельницей»,
«теоремой – бабочкой»
или
«теоремой невесты»
Сейчас известно около 150 различных доказательств этой теоремы (геометрических, алгебраических, механических и т.д.) Поэтому теорема Пифагора занесена в «Книгу рекордов Гиннеса».
так как некоторые «убогие» ученики, не имевшие серьезной математической подготовки, бежали от геометрии. Слабые ученики, заучившие теоремы наизусть, без понимания, и прозванные поэтому «ослами», были не в состоянии преодолеть теорему Пифагора, служившую для них вроде непреодолимого моста.
и называлось:
Слайд 11Самое простое доказательство
Рассмотрим квадрат, показанный на рисунке.
Сторона квадрата равна a
+ c.
В одном случае (слева) квадрат разбит на квадрат
со стороной b и четыре прямоугольных треугольника с катетами a и c.В другом случае (справа) квадрат разбит на два квадрата со сторонами a и c и четыре прямоугольных треугольника с катетами a и c.
Таким образом, получаем, что площадь квадрата со стороной b равна сумме площадей квадратов со сторонами a и c.
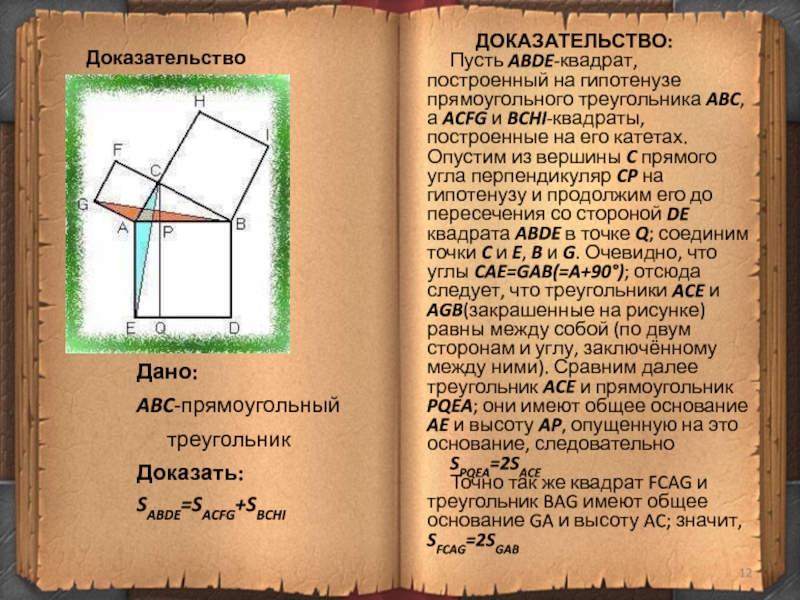
Слайд 12Доказательство Евклида
Дано:
ABC-прямоугольный треугольник
Доказать:
SABDE=SACFG+SBCHI
ДОКАЗАТЕЛЬСТВО:
Пусть ABDE-квадрат, построенный на гипотенузе
прямоугольного треугольника ABC, а ACFG и BCHI-квадраты, построенные на его
катетах. Опустим из вершины C прямого угла перпендикуляр CP на гипотенузу и продолжим его до пересечения со стороной DE квадрата ABDE в точке Q; соединим точки C и E, B и G. Очевидно, что углы CAE=GAB(=A+90°); отсюда следует, что треугольники ACE и AGB(закрашенные на рисунке) равны между собой (по двум сторонам и углу, заключённому между ними). Сравним далее треугольник ACE и прямоугольник PQEA; они имеют общее основание AE и высоту AP, опущенную на это основание, следовательноSPQEA=2SACE
Точно так же квадрат FCAG и треугольник BAG имеют общее основание GA и высоту AC; значит, SFCAG=2SGAB
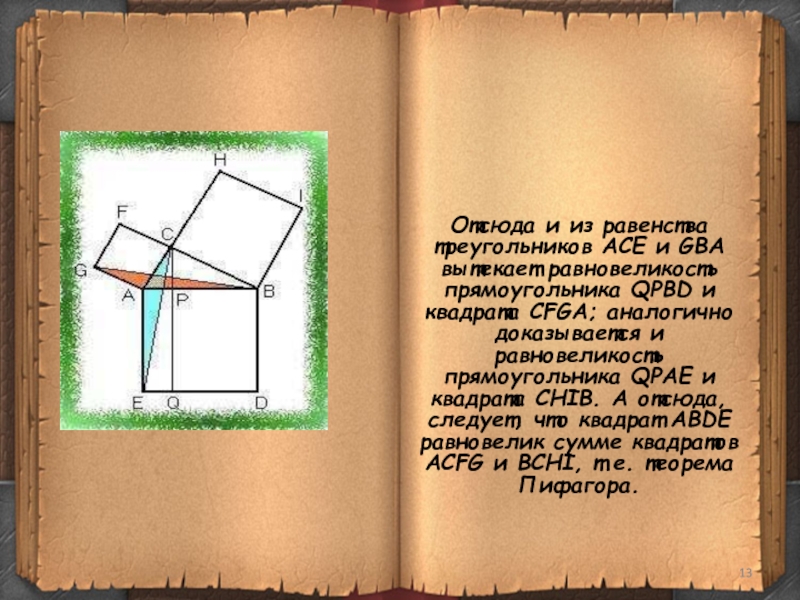
Слайд 13Отсюда и из равенства треугольников ACE и GBA вытекает равновеликость
прямоугольника QPBD и квадрата CFGA; аналогично доказывается и равновеликость прямоугольника
QPAE и квадрата CHIB. А отсюда, следует, что квадрат ABDE равновелик сумме квадратов ACFG и BCHI, т.е. теорема Пифагора.Слайд 14Алгебраическое доказательство
Дано: ABC-прямоугольный треугольник
Доказать: AB2=AC2+BC2
Доказательство:
1) Проведем высоту CD из вершины прямого
угла С.
2) По определению косинуса угла соsА=AD/AC=AC/AB, отсюда следует
AB*AD=AC2.
3) Аналогично соsВ=BD/BC=BC/AB,
значит AB*BD=BC2.
4) Сложив полученные равенства почленно, получим:
AC2+BC2=АВ*(AD + DB)
AB2=AC2+BC2. Что и требовалось доказать.
Слайд 15Геометрическое доказательство
Дано: ABC-прямоугольный треугольник
Доказать: BC2=AB2+AC2
Доказательство:
1) Построим отрезок CD равный отрезку
AB на продолжении катета AC прямоугольного треугольника ABC. Затем опустим
перпендикуляр ED к отрезку AD, равный отрезку AC, соединим точки B и E. 2) Площадь фигуры ABED можно найти, если рассматривать её как сумму площадей трёх треугольников:SABED=2*AB*AC/2+BC2/2
3) Фигура ABED является трапецией, значит, её площадь равна:
SABED= (DE+AB)*AD/2.
4) Если приравнять левые части найденных выражений, то получим:
AB*AC+BC2/2=(DE+AB)(CD+AC)/2
AB*AC+BC2/2= (AC+AB)2/2
AB*AC+BC2/2= AC2/2+AB2/2+AB*AC
BC2=AB2+AC2.
Это доказательство было опубликовано в 1882 году Гэрфилдом.
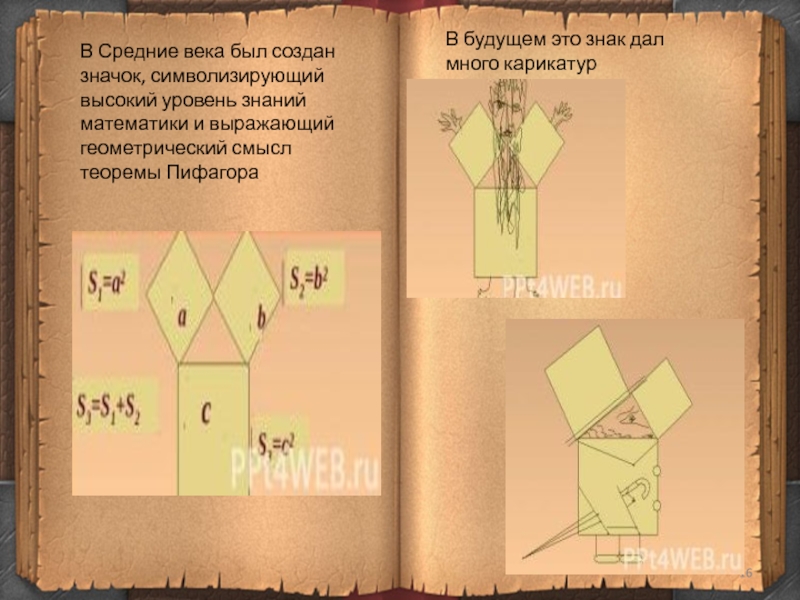
Слайд 16В Средние века был создан значок, символизирующий высокий уровень знаний
математики и выражающий геометрический смысл теоремы Пифагора
В будущем это знак
дал много карикатурСлайд 20В настоящее время известно, что эта теорема не была открыта
Пифагором. Однако одни полагают, что Пифагор первым дал ее полноценное
доказательство, а другие отказывают ему и в этой заслуге. Некоторые приписывают Пифагору доказательство, которое Евклид приводит в первой книге своих "Начал". С другой стороны, Прокол утверждает, что доказательство в "Началах" принадлежит самому Евклиду. Как мы видим, история математики почти не сохранила достоверных данных о жизни Пифагора и его математической деятельности. Зато легенда сообщает даже ближайшие обстоятельства, сопровождавшие открытие теоремы. Многим известен сонет Шамиссо:
Пребудет вечной истина, как скоро
Ее познает слабый человек!
И ныне теорема Пифагора
Верна, как и в его далекий век.
Обильно было жертвоприношенье
Богам от Пифагора. Сто быков
Он отдал на закланье и сожженье
За света луч, пришедший с облаков. Поэтому всегда с тех самых пор,
Чуть истина рождается на свет,
Быки ревут, ее почуя ,вслед.
Они не в силах свету помешать ,
А могут лишь закрыв глаза дрожать
От страха, что вселил в них Пифагор.
Слайд 21
Ты же будь твёрдым: божественный род присутствует в смертных,
Им,
возвещая, священная всё открывает природа.
Если не чуждо это тебе,
ты наказы исполнишь,Душу свою исцелишь и от множества бедствий избавишь.
Яства, сказал я, оставь те, что я указал в очищеньях
И руководствуйся подлинным знанием — лучшим возничим.
Если ты, тело покинув, в свободный эфир вознесёшься,
Станешь нетленным, и вечным, и смерти не знающим богом.
ПИФАГОР