Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация факультативного занятия Логарифмические неравенства
Содержание
- 1. Презентация факультативного занятия Логарифмические неравенства
- 2. СодержаниеПояснительная запискаДидактические целиПланированиеОбоснование проекта одного из факультативных занятий по теме «Логарифмические неравенства»Проект занятияПодведение итогов (рефлексия)Литература
- 3. Пояснительная записка С точки зрения вычислительной
- 4. Дидактические целиОбразовательные: Систематизировать, обобщить и углубить знания
- 5. Учебно-тематическое планирование Алгебра и начала анализа.10 класс
- 6. Обоснование проекта одного из факультативных занятий по
- 7. Проект занятияАктуальность:Умения решать сложные неравенства в процессе
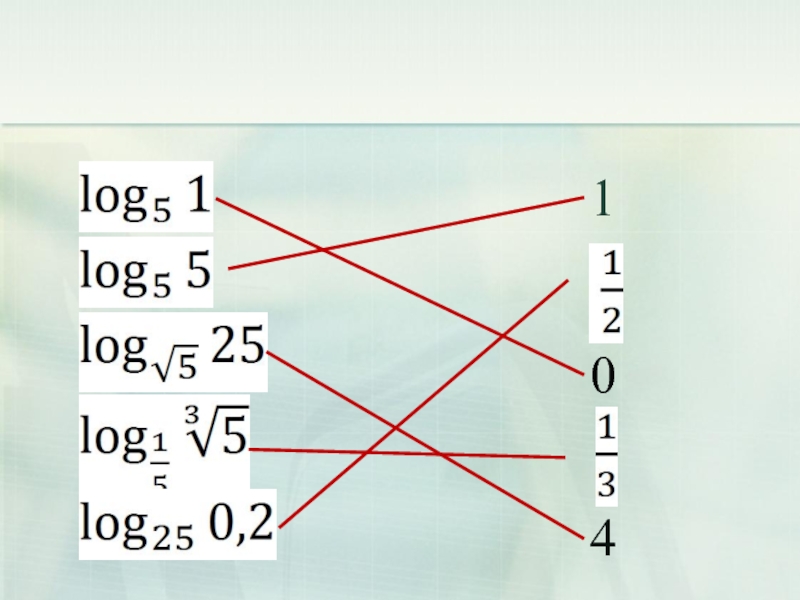
- 8. Ход занятия 1. Актуализация опорных знаний.1)Найди соответствия: - - 4104
- 9. - - 104
- 10. 2) Найди область определения и установи соответствия: x1 x>0 x≠0 x
- 11. x1 x>0 x≠0 x
- 12. 3) Найди ошибку: >> >3 > 4 3>41)2)3)4)5)
- 13. 3
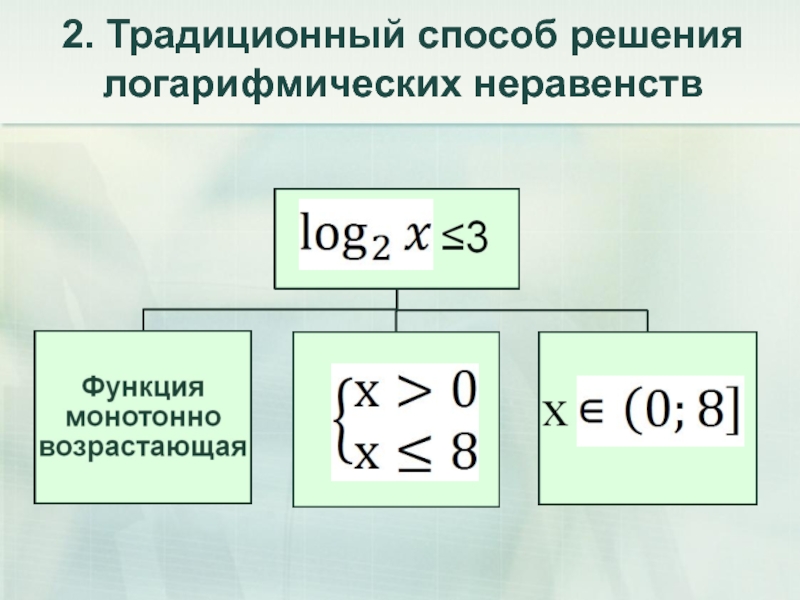
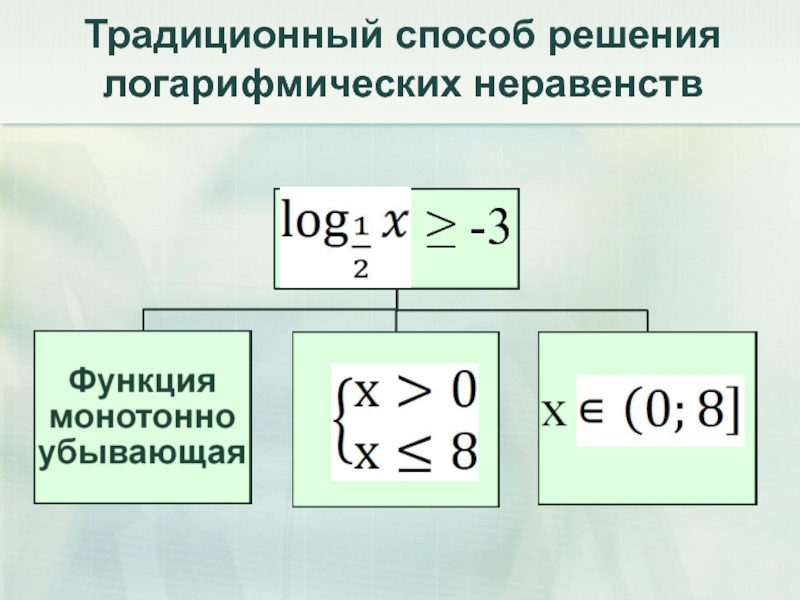
- 14. 2. Традиционный способ решения логарифмических неравенств
- 15. Традиционный способ решения логарифмических неравенств ≥ -3
- 16. 3. Решение неравенств способом рационализации (теоретическая часть)
- 17. Алгоритм решения задачи 1
- 18. 2) Модель задачиПравило 2: Знак разности совпадает со знаком произведения(a-1)(A-B) в ОДЗ.> - > 0-
- 19. Алгоритм решения задачи 2
- 20. 3) Модель задачи Знак первого множителя
- 21. Алгоритм решения задачи 3
- 22. 4) Модель задачи Решение неравенства
- 23. Алгоритм решения задачи 4 >0 (≥0)
- 24. 4. Решение неравенств (практическая часть) 1) Решите неравенство: ≤
- 25. Проверь себя:
- 26. 2) Решите неравенство:● ≥ 0
- 27. Проверь себя:
- 28. 3) Решите неравенство:● ≤ 0
- 29. Проверь себя:
- 30. 4) Решите неравенство: ≤ 1
- 31. Проверь себя:≤ 0≤ 0
- 32. 5. Задания для самостоятельного решения 1) Сколько целых решений имеют неравенства: ● ≤ 02)4)3)< 0≤ 15)
- 33. Подведение итогов(рефлексия)1. Познакомились с новым способом решения
- 34. ЛитератураАлимов Ш.А. и др. «Алгебра и начала
- 35. Скачать презентанцию
СодержаниеПояснительная запискаДидактические целиПланированиеОбоснование проекта одного из факультативных занятий по теме «Логарифмические неравенства»Проект занятияПодведение итогов (рефлексия)Литература
Слайды и текст этой презентации
Слайд 1Алгебра 10 класс
Факультативное занятие
по теме
«Логарифмические неравенства»
Надежкина Ирина
Геннадьевна
Слайд 2Содержание
Пояснительная записка
Дидактические цели
Планирование
Обоснование проекта одного из факультативных занятий по теме
«Логарифмические неравенства»
Проект занятия
Подведение итогов (рефлексия)
Литература
Слайд 3Пояснительная записка
С точки зрения вычислительной практики, изобретение логарифмов
по важности можно смело поставить рядом с другим, более древним
изобретением индусов - нашей десятичной системой нумерации.Успенский Я.В.
В современной школе основной формой обучения математике, главным связующим звеном в интеграции различных организационных форм обучения по-прежнему остается урок, но при отведенных 2,5 ч. изучение тем, представленных на ЕГЭ, без факультативных занятий не представляется возможным.
В процессе обучения математический материал осознается и усваивается преимущественно в процессе решения задач, поэтому на уроках и факультативах теория не изучается в отрыве от практики. Для того, чтобы успешно решать логарифмические уравнения и неравенства, необходимо уверенное владение формулами для логарифмов и свойствами логарифмических функций.
Ситуация несколько осложняется, например, по сравнению с показательными уравнениями и неравенствами, наличием ограничений, поэтому необходимо внимательно следить за равносильностью совершаемых преобразований.
Слайд 4Дидактические цели
Образовательные:
Систематизировать, обобщить и углубить знания по теме «Логарифмическая
функция».
Ознакомить и закрепить способы решения логарифмических уравнений и неравенств.
Предоставить возможность
обучающимся проверить свои знания и повысить их уровень.Развивающие:
Развить математическое мышление, речь, способности переводить теоретические знания в практические навыки, формировать навыки самообучения, самоорганизации и самооценки, способствовать развитию творческой деятельности учащихся.
Воспитательные:
Воспитывать познавательную активность, сознательное отношение к восприятию материала и ответственное отношение к труду.
Воспитывать волю и настойчивость для достижения конечных результатов.
Воспитывать любовь и уважение к предмету.
Слайд 5Учебно-тематическое планирование Алгебра и начала анализа.10 класс (2,5 часа в неделю, всего
86 часов)
Глава 4. Логарифмическая функция (15 часов)
Слайд 6Обоснование проекта одного из факультативных занятий по теме «Логарифмические неравенства»
Выбор
факультативной формы занятия по теме «Логарифмические неравенства», представленной в материалах
ЕГЭ (С 3), обусловлен недостаточным количеством часов (3 часа), отведенных на эту тему.Кроме этого, практика экзаменов показывает, что наибольшую сложность для школьников представляют трансцендентные неравенства. При их решении методом интервалов вычисление значений функций в промежуточных точках может вызвать трудности вычислительного характера. Чтобы устранить эти проблемы и расширить возможности применения метода интервалов при решении трансцендентных неравенств используется идея рационализации неравенств (метод декомпозиции или метод замены множителей). Использование этого способа, по сравнению с традиционным, даже при решении простейших неравенств может иметь преимущество в том, что не надо писать заключения о той или другой монотонности. Этот метод особенно выгоден, когда рассматривается неравенство с переменным основанием, нет необходимости думать о том, большим или меньшим единицы оно является. Это особенно важно при решении тестов ЕГЭ, когда время для их решения ограничено.
Слайд 7Проект занятия
Актуальность:
Умения решать сложные неравенства в процессе подготовки к ЕГЭ
необходимы каждому ученику
Цель. Обеспечить условия:
Для нахождения различных способов решения логарифмических
неравенствДля преодоления причин, затрудняющих формирование у учащихся умений и способностей в решении логарифмических неравенств
Для рефлексивной деятельности учащихся на каждом этапе
Создание ситуации успеха и развития интереса к изучаемой теме
Задачи. Создать условия:
Для обучения учащихся решению сложных логарифмических неравенств
Для знакомства с новыми способами решения неравенств
Слайд 163. Решение неравенств способом рационализации (теоретическая часть)
1) Модель задачи
ОДЗ: A>0
Если a>1, то >0 (<0), тогда и только тогда , когда А>1 (<1), т.е. (a-1)(A-1) >0 (<0)
Если 0
И, наоборот, если (a-1)(A-1) >0 (<0), то:
При a>1 имеем A>1 (<1), а тогда >0 (<0);
При 0
Следовательно, имеет место условие равносильности
>0 (<0) ↔ (a-1)(A-1) >0 (<0)
Правило 1: Знак совпадает со знаком произведения
(a-1)(A-1) в ОДЗ.
>0 (<0)
ОДЗ
Слайд 182) Модель задачи
Правило 2:
Знак разности
совпадает со знаком произведения
(a-1)(A-B)
в ОДЗ.
>
-
> 0
-
Слайд 203) Модель задачи
Знак первого множителя совпадает со знаком
произведения (a-1)(A-1) в ОДЗ.
Знак второго множителя совпадает
со знаком произведения (b-1)(B-1) в ОДЗ.●
≤ 0
Слайд 224) Модель задачи
Решение неравенства определяется знаками множителей.
Воспользуемся тем, что в ОДЗ знак разности
-совпадает со знаком произведения , а знак совпадает в ОДЗ со знаком . Поэтому:
> 0 (≥ 0)
>0 (≥0) ↔
>0 (≥0)
ОДЗ
Слайд 325. Задания для самостоятельного решения
1) Сколько целых решений имеют
неравенства:
●
≤ 0
2)
4)
3)
< 0
≤ 1
5)
Слайд 33Подведение итогов(рефлексия)
1. Познакомились с новым способом решения
логарифмических неравенств.
2. Научились применять его на практике.
3.
Оценили преимущества нового способа, особенно при решении неравенств с неизвестным в основании логарифма.4. Стали чувствовать себя увереннее при решении более сложных неравенств.
5. Анализ контрольной работы по теме «Логарифмическая функция» показал, что учащиеся, посещающие занятия факультатива, показали более высокий процент качества.
Слайд 34Литература
Алимов Ш.А. и др. «Алгебра и начала анализа 10-11 класс»-учебник.
М.Просвещение, 2010
Колесников С.И. «Математика. Интенсивный курс подготовки к ЕГЭ» М.Айрис
Пресс, 2008Парфёнов В.С., Сергеев И.Н. «Отличник ЕГЭ. Математика. Решение сложных задач» М.Интеллект-Центр, 2010
Учебно-методический комплекс «Математика. Подготовка к ЕГЭ-2012». Под ред. Ф.Ф.Лысенко. Ростов-на-Дону. Легион-М,2011
«ЕГЭ-2012. Математика. Типовые экзаменационные варианты» под ред. А.Л.Семёнова, И.В.Ященко. М. Национальное образование, 2011
Журнал «Математика в школе» 06/ 2011
Газета «Математика» 12/2011