Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация к обобщающему уроку по теме "Тригонометрические уравнения"
Содержание
- 1. Презентация к обобщающему уроку по теме "Тригонометрические уравнения"
- 2. Повторить, систематизировать и углубить знания о методах решения тригонометрических уравнений.Цель урока
- 3. "Мне приходится делить время между политикой и
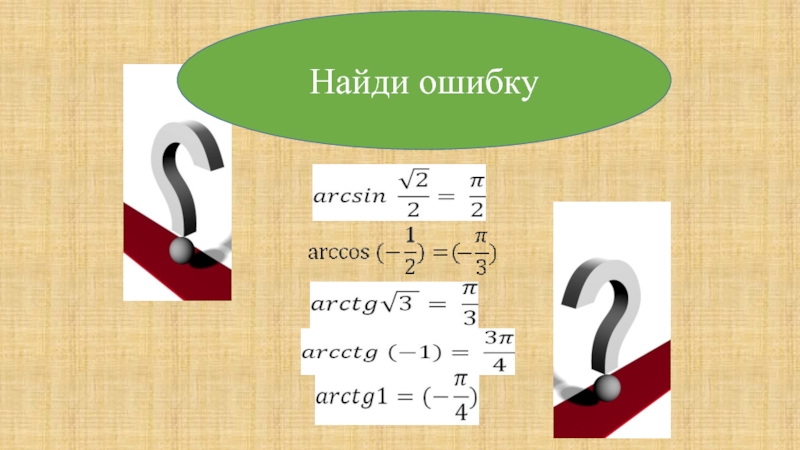
- 4. Найди ошибку
- 5. Установи соответствие
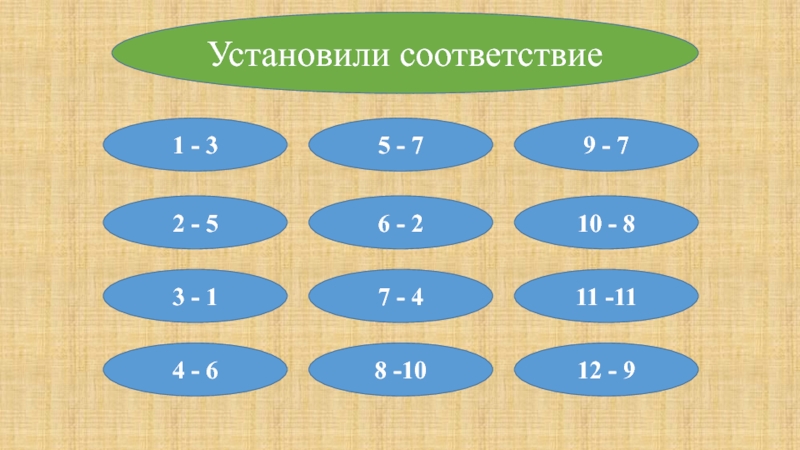
- 6. Установили соответствие1 - 32 - 55 -
- 7. Методы решения тригонометрических уравнений1.Алгебраический ( метод замены
- 8. Определи метод решения уравнения
- 9. Историческая страничкаСлово тригонометрия происходит от двух греческих
- 10. Историческая страничкаСинус – латинское слово и означает
- 11. Задание на дом
- 12. «Считай несчастным тот день или тот час,
- 13. Слайд 13
- 14. Скачать презентанцию
Повторить, систематизировать и углубить знания о методах решения тригонометрических уравнений.Цель урока
Слайды и текст этой презентации
Слайд 2Повторить, систематизировать и углубить знания о методах решения тригонометрических уравнений.
Цель
урока
Слайд 3"Мне приходится делить время между политикой и уравнениями. Однако уравнения,
по-моему, гораздо важнее. Политика существует только для данного момента, а
уравнения будут существовать вечно".А. Эйнштейн.
Слайд 7Методы решения тригонометрических уравнений
1.Алгебраический ( метод замены переменной)
2. Разложение на
множители
3. Приведение к однородному
4. С помощью тригонометрических формул
Слайд 9Историческая страничка
Слово тригонометрия происходит от двух греческих слов: тригонон –
треугольник и метрейн – измерять и в буквальном переводе означает
измерение треугольников.Градусное измерение углов возникло в Древнем Вавилоне (в середине II тысячелетия до нашей эры). Вавилонская система измерения углов оказалась достаточно удобной, и ее применяли и сохранили математики Древней Греции и Рима (Гиппарх, Птолемей, Пифагор).
Принятая сегодня система обозначения величин углов получила широкое распространение на рубеже XVI–XVII веков; ею уже пользовались известные астрономы Николай Коперник и Тихо Браге.
Гиппарх
Птолемей
Пифагор
Николай Коперник
Тихо Браге
Слайд 10Историческая страничка
Синус – латинское слово и означает изгиб, кривизна; косинус
– «дополнительный синус» или синус дополнительной дуги (cosα = sin(90°
– α)).Термины «тангенс» (в буквальном переводе – «касающийся») и «котангенс» произошли от латинского языка и появились в Европе значительно позднее. Среднеазиатские ученые называли соответствующие линии «тенями»: котангенс – «первой тенью», тангенс – «второй тенью».
Современный вид тригонометрия получила благодаря крупнейшему математику XVIII столетия Леонарду Эйлеру (1707 – 1783), швейцарцу по происхождению. Долгие годы он работал в России и являлся членом Петербургской Академии наук. Именно Эйлер впервые ввел известные определения тригонометрических функций, стал рассматривать функции произвольного угла, получил формулы приведения.
Слайд 12«Считай несчастным тот день или тот час, в которой ты
не усвоил ничего нового и ничего не прибавил к своему
воображению."Я.А. Коменский.
