Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация к проблемному уроку по теме "Теорема Пифагора"
Содержание
- 1. Презентация к проблемному уроку по теме "Теорема Пифагора"
- 2. Слайд 2
- 3. Слайд 3
- 4. Слайд 4
- 5. Слайд 5
- 6. Слайд 6
- 7. Теорема Пифагора В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетовc²=a²+b²
- 8. Расположим четыре равных прямоугольных треугольника так, как
- 9. Пусть ABC есть прямоугольный треугольник с
- 10. Пифагор Самосский (570—490 гг. до н. э.)древнегреческий философ и математик, создатель религиозно-философской школы пифагорейцев
- 11. Биография Родителями Пифагора были Мнесарх и
- 12. Учение Пифагора следует разбить на
- 13. Теорема Пифагора на практикеВ романской архитектуре часто
- 14. В конце девятнадцатого века высказывались разнообразные предположения
- 15. Задачи 1. Над озером тихим,
- 16. 3. Задача индийского математика XII века Бхаскары
- 17. ВыводыТеорема Пифагора - одна из главных и,
- 18. Скачать презентанцию
Слайды и текст этой презентации
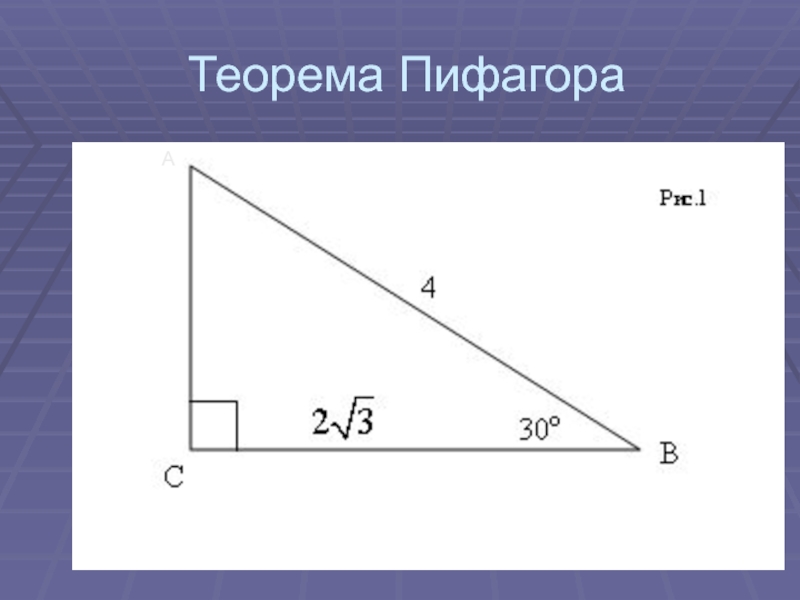
Слайд 7Теорема Пифагора
В прямоугольном треугольнике квадрат длины гипотенузы равен
сумме квадратов длин катетов
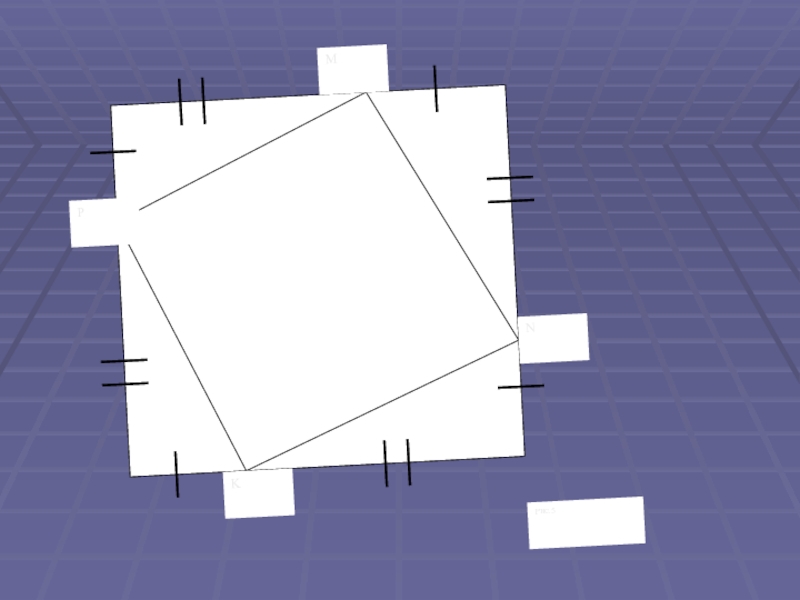
Слайд 8Расположим четыре равных прямоугольных треугольника так, как показано на рисунке.
2.
Четырёхугольник со сторонами c является квадратом, так как сумма двух
острых углов 90°, а развёрнутый угол — 180°.3. Площадь всей фигуры равна, с одной стороны, площади квадрата со стороной (a+b), а с другой стороны, сумме площадей четырёх треугольников и площади внутреннего квадрата.
Через равнодополняемость
Доказательство
Слайд 9 Пусть ABC есть прямоугольный треугольник с прямым углом C.
Проведём высоту из C и обозначим её основание через H.
Треугольник ACH подобен треугольнику ABC по двум углам. Аналогично, треугольник CBH подобен ABC. Введя обозначенияполучаем
Что эквивалентно
Сложив, получаем
или
Через подобные треугольники
Слайд 10Пифагор Самосский
(570—490 гг. до н. э.)
древнегреческий философ и математик,
создатель религиозно-философской школы пифагорейцев
Слайд 11Биография
Родителями Пифагора были Мнесарх и Партенида с Самоса.
Рождение ребёнка будто бы предсказала Пифия в Дельфах, потому Пифагор
и получил своё имя, которое значит «тот, о ком объявила Пифия».Пифагор в 18-летнем возрасте покинул родной остров и, объехав мудрецов в разных краях света, добрался до Египта, где пробыл 22 года, пока его не увёл в Вавилон в числе пленников персидский царь Камбиз, завоевавший Египет в 525 до н. э. В Вавилоне Пифагор пробыл ещё 12 лет, общаясь с магами, пока наконец не смог вернуться на Самос в 56-летнем возрасте, где соотечественники признали его мудрым человеком.
Слайд 12 Учение Пифагора следует разбить на две составляющие части:
научный подход к познанию мира и религиозно-оккультный образ жизни, проповедуемый
Пифагором. Доподлинно неизвестны заслуги Пифагора в первой части, так как ему позднее приписывали всё, созданное последователями в рамках школы пифагореизма. Вторая часть превалирует в учении Пифагора, и именно она осталась в сознании большинства античных авторов.
Слайд 13Теорема Пифагора на практике
В романской архитектуре часто встречается мотив, представленный
на рисунке. Если b по-прежнему обозначает ширину окна, то радиусы
полуокружностей будут равны R = b / 2 и r = b / 4. Радиус p внутренней окружности можно вычислить из прямоугольного треугольника, изображенного на рис. пунктиром. Гипотенуза этого треугольника, проходящая через точку касания окружностей, равна b/4+p, один катет равен b/4, а другой b/2-p. По теореме Пифагора имеем:(b/4+p)=( b/4)+( b/4-p)
или
b/16+ bp/2+p=b/16+b/4-bp+p,
откуда
bp/2=b/4-bp.
Разделив на b и приводя подобные члены, получим:
(3/2)p=b/4, p=b/6.
Слайд 14В конце девятнадцатого века высказывались разнообразные предположения о существовании обитателей
Марса подобных человеку, это явилось следствием открытий итальянского астронома Скиапарелли
(открыл на Марсе каналы которые долгое время считались исскуственными) и др.Естественно, что вопрос о том, можно ли с помощью световых сигналов объясняться с этими гипотетическими существами, вызвал оживленную дискуссию. Парижской академией наук была даже установлена премия в 100000 франков тому, кто первый установит связь с каким-нибудь обитателем другого небесного тела; эта премия все еще ждет счастливца. В шутку, хотя и не совсем безосновательно , было решено передать обитателям Марса сигнал в виде теоремы Пифагора.
Слайд 15Задачи
1. Над озером тихим,
С полфута
размером, высился лотоса цвет.
Он рос одиноко. И ветер
порывомОтнёс его в сторону. Нет
Боле цветка над водой.
Нашёл же рыбак его ранней весной
В двух футах от места, где рос.
Итак, предложу я вопрос:
Как озера вода здесь глубока.
( 3 3/4 фута)
2. Из учебника"Арифметика" на Руси.
Случися некоему человеку к стене лествицу прибрати, стены же тоя высота есть 117 стоп.
И обрете лествицу долготою 125 стоп. И ведати хощет, колико стоп сея лествицы нижний конец
от стены отстояти имать.
(44 стопы)
Слайд 163. Задача индийского математика XII века Бхаскары
На берегу
реки рос тополь одинокий.
Вдруг ветра порыв его ствол надломал.
Бедный тополь упал. И угол прямойС теченьем реки его ствол составлял.
Запомни теперь, что в том месте река
В четыре лишь фута была широка.
Верхушка склонилась у края реки.
Осталось три фута всего от ствола,
Прошу тебя, скоро теперь мне скажи:
У тополя как велика высота? (3+5 футов)
Слайд 17Выводы
Теорема Пифагора - одна из главных и, можно сказать, самая
главная теорема геометрии. Теорема Пифагора замечательна тем, что сама по
себе она вовсе не очевидна. Например, свойства равнобедренного треугольника можно видеть непосредственно на чертеже. Но сколько ни смотри на прямоугольный треугольник, никак не увидишь, что между его сторонами есть простое соотношение: . Уникальна не только теорема Пифагора, но и то, как широко она применяется. Очень интересна и биография Пифагора.Сам факт, что Пифагор - это не имя, а прозвище, которое философ получил за то, что всегда говорил верно и убедительно, как греческий оракул. (Пифагор - "убеждающий речью".) Своими речами приобрёл 2000 учеников, которые вместе со своими семьями образовали школу-государство, где действовали законы и правила Пифагора. Хотя это были лишь современники, а что говорить о них, если она уже на протяжениии многих веков завораживает всё человечество своей красотой и лаконичностью.
c²=a²+b²