Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация к уроку геометрии 8 класс на тему "Средняя линия"
Содержание
- 1. Презентация к уроку геометрии 8 класс на тему "Средняя линия"
- 2. СодержаниеСредняя линия треугольникаСредняя линия трапецииЗадачи
- 3. Средняя линия треугольника
- 4. Средняя линия треугольника.Определение:Отрезок, соединяющий середины двух сторон треугольника, называют СРЕДНЕЙ ЛИНИЕЙ ТРЕУГОЛЬНИКА.
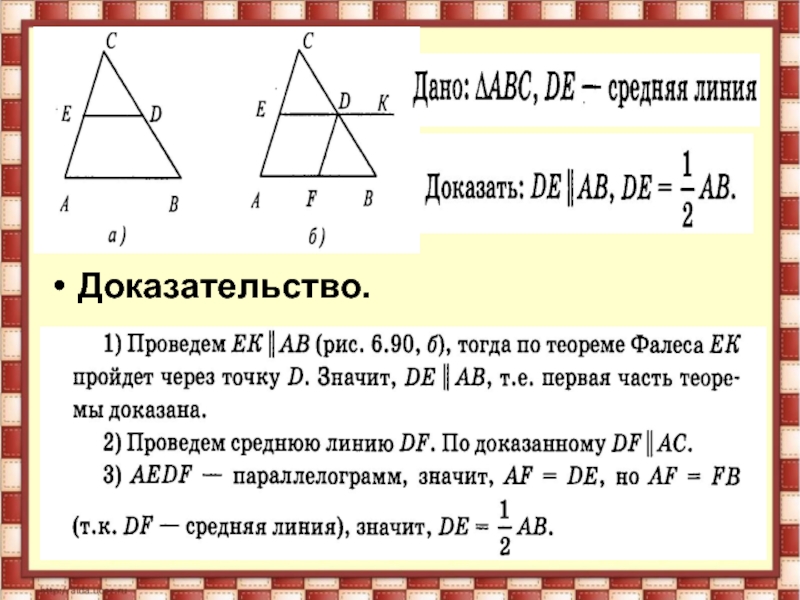
- 5. Теорема Средняя линия треугольника, соединяющая середины
- 6. Доказательство.
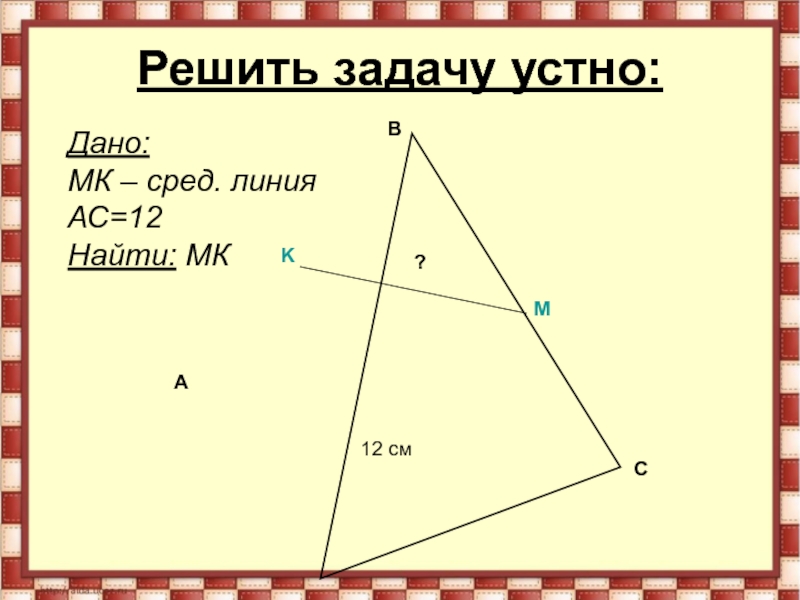
- 7. Решить задачу устно:ABCKM12 смДано: MК – сред. линияАС=12Найти: MК ?
- 8. Работа в парах:
- 9. Решим задачу :Дано: MN – сред. линияНайти: P∆АВСMNABC3 43,5
- 10. Работа в парах:
- 11. Самостоятельная работаДано: AC║EF; EB =4; EF =12; FC =5Найти: PABCАВСEF
- 12. Решим задачуДано: СD║BE║MK; AD =16; CD =10;MB=4Найти: PAMKАBCDEKM
- 13. Средняя линия трапеции
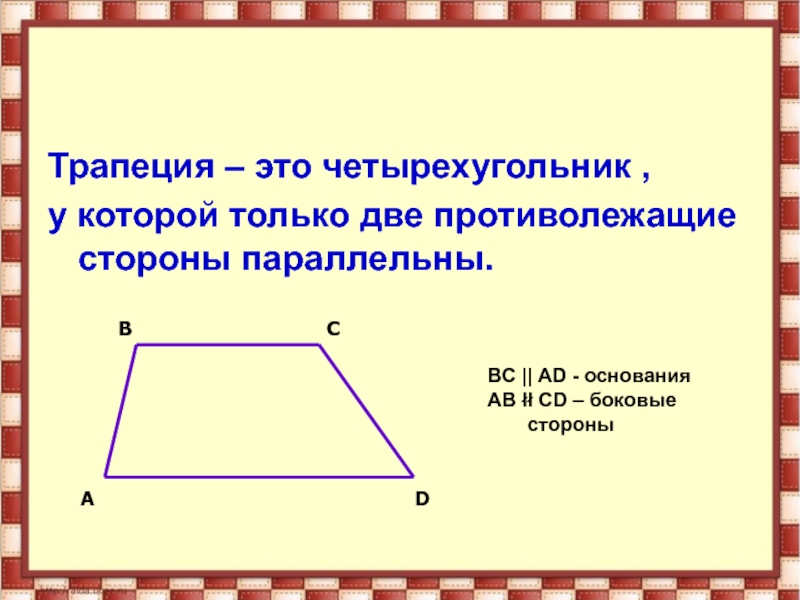
- 14. Трапеция – это четырехугольник , у которой
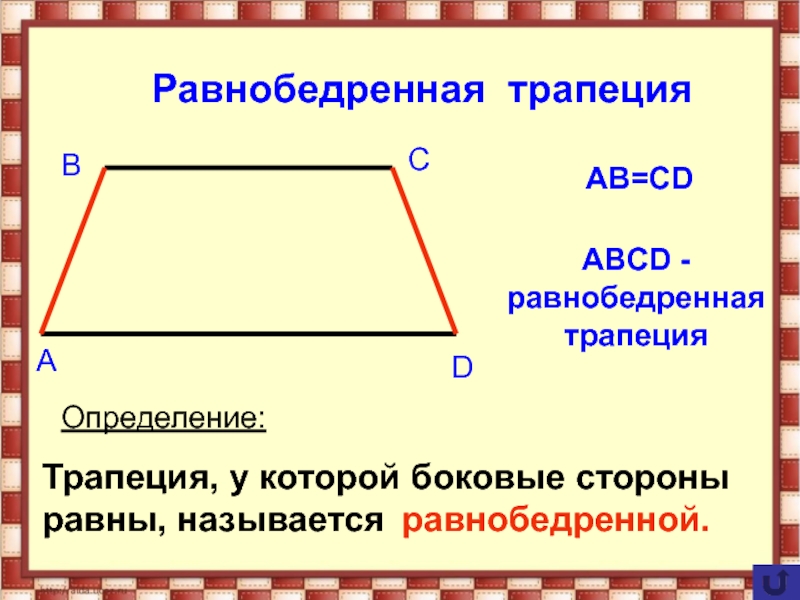
- 15. Равнобедренная трапецияОпределение:Трапеция, у которой боковые стороны равны, называется равнобедренной.AB=CDABCD - равнобедренная трапеция
- 16. Прямоугольная трапецияОпределение:Трапеция, у которой один из углов прямой, называется прямоугольной.ABCD - прямоугольная трапеция
- 17. Средняя линия трапеции. Определение: Средней линией трапеции
- 18. Теорема о средней линии трапеции Средняя линия
- 19. Слайд 19
- 20. Решить устно:6,3 см18,7 см?
- 21. Решить устно в парах:Дано: AB = 16
- 22. СПАСИБО ЗА УРОК !!!
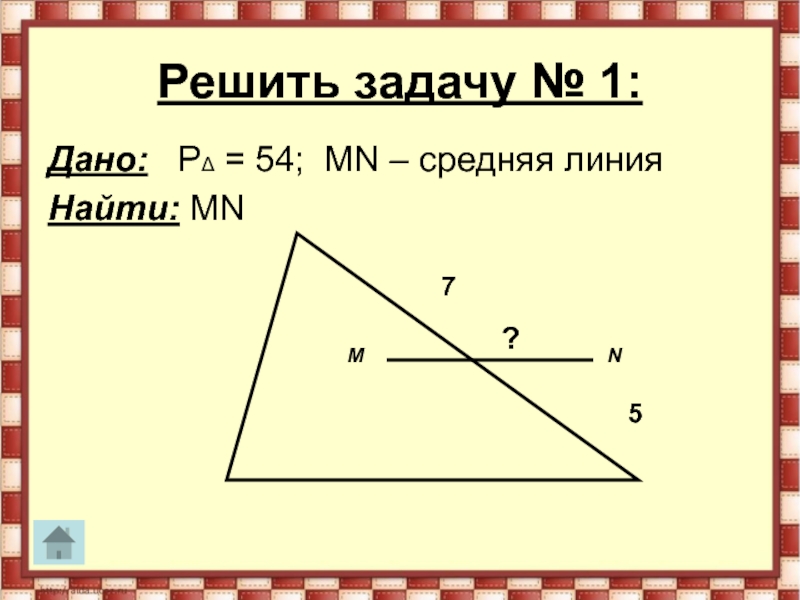
- 23. Решить задачу № 1:Дано: PΔ = 54; MN – средняя линияНайти: MNMN7 5 ?
- 24. Решить задачу № 2Дано: АВСD-трапеция; MN -
- 25. Решить задачу № 3Дано: MN - средняя
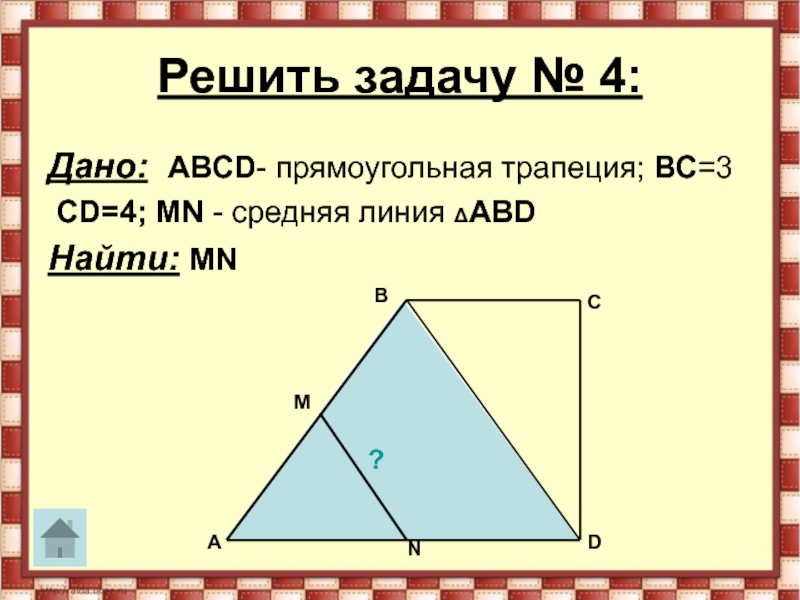
- 26. Решить задачу № 4:Дано: АВСD- прямоугольная трапеция; ВС=3 СD=4; MN - средняя линия ΔАВDНайти: MNMNАСDВ?
- 27. Решить задачу № 5Дано: ΔАВС подобен ΔВDК;
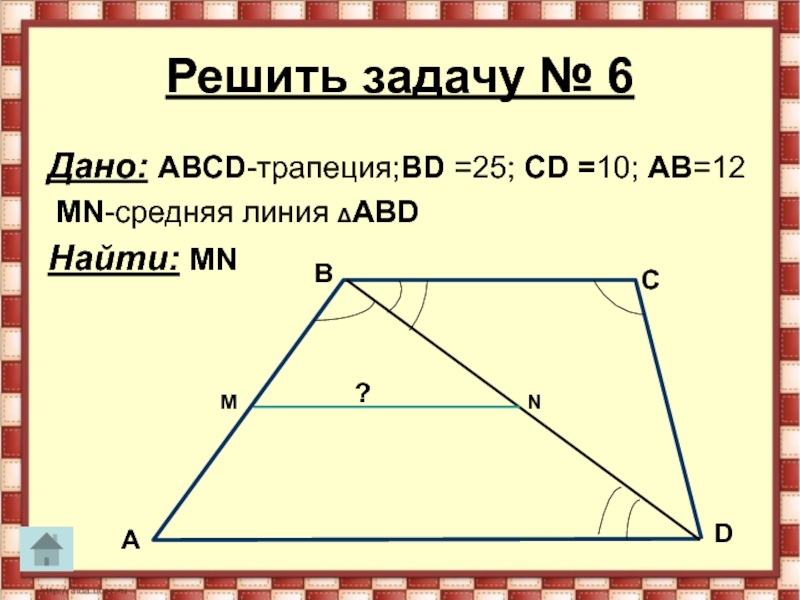
- 28. Решить задачу № 6Дано: АВСD-трапеция;ВD =25; СD =10; АВ=12 MN-средняя линия ΔАВD Найти: MN AВСDMN?
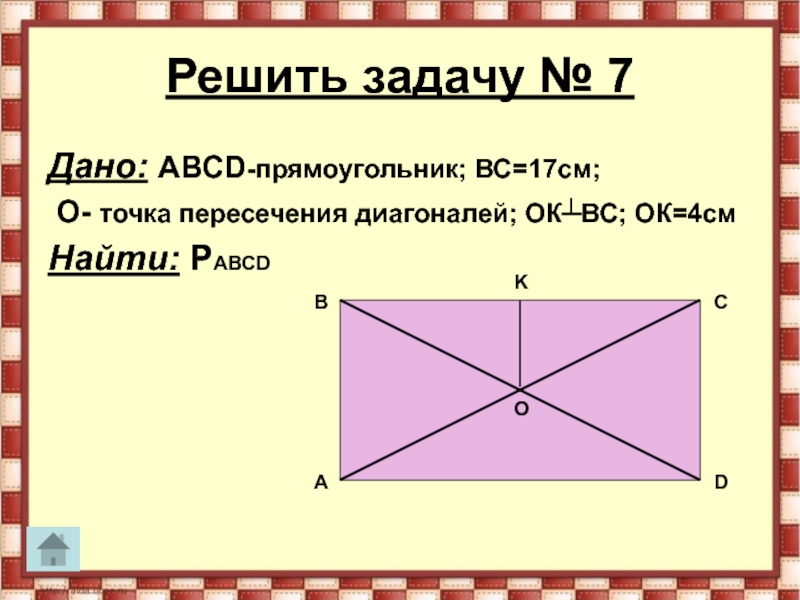
- 29. Решить задачу № 7Дано: АВСD-прямоугольник; ВС=17см; О- точка пересечения диагоналей; ОК┴ВС; ОК=4см Найти: PАВСDВАСDKO
- 30. Задача № 8.Дан прямоугольный треугольник АВС. Гипотенуза
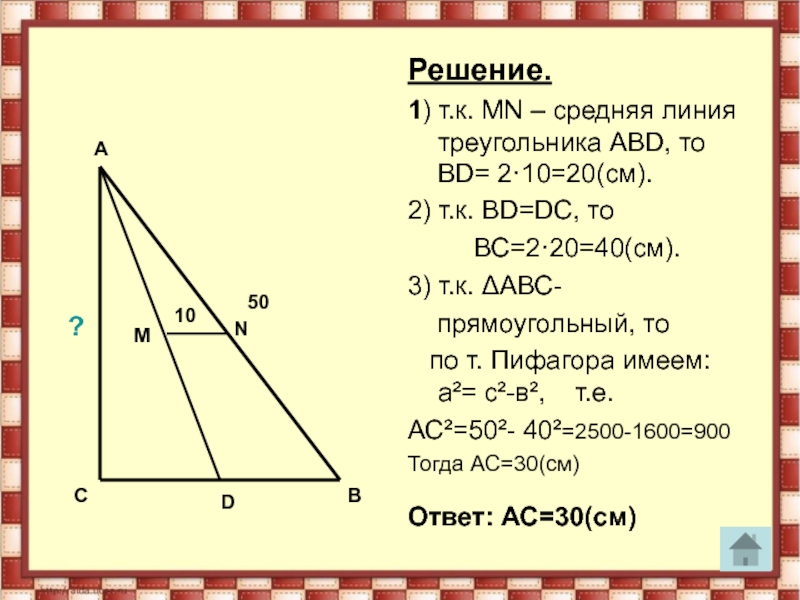
- 31. Решение. 1) т.к. МN – средняя линия
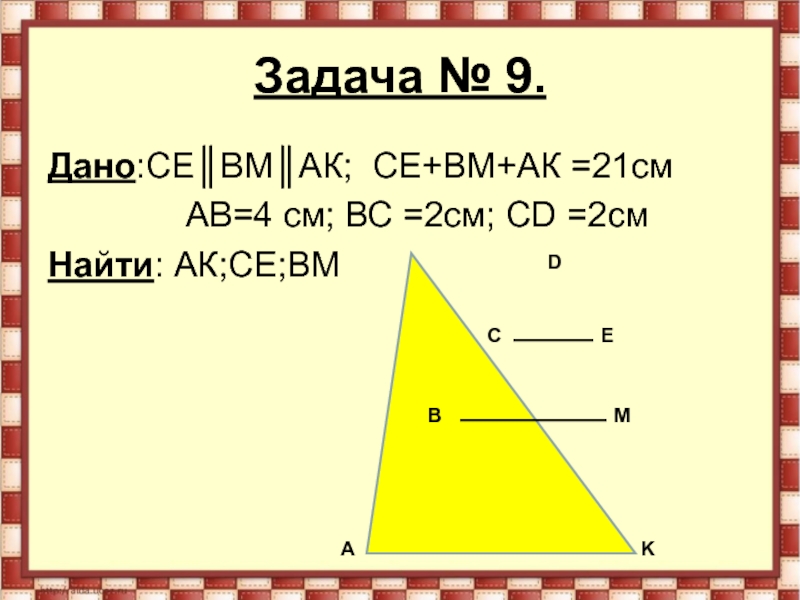
- 32. Задача № 9.Дано:СЕ║ВМ║АК; СЕ+ВМ+АК =21см
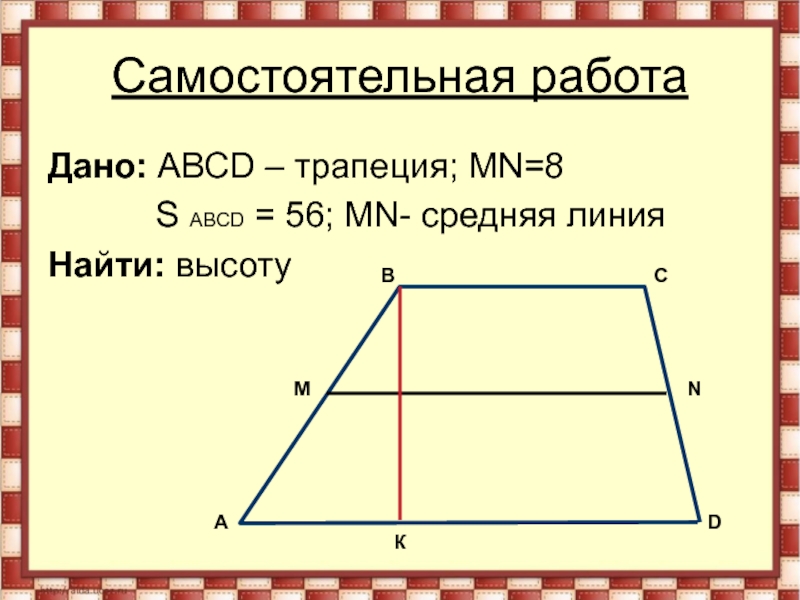
- 33. Самостоятельная работаДано: АВСD – трапеция; MN=8
- 34. СПАСИБО ЗА УРОК !!!
- 35. Скачать презентанцию
СодержаниеСредняя линия треугольникаСредняя линия трапецииЗадачи
Слайды и текст этой презентации
Слайд 4Средняя линия треугольника.
Определение:
Отрезок, соединяющий середины двух сторон треугольника, называют
СРЕДНЕЙ ЛИНИЕЙ ТРЕУГОЛЬНИКА.
Слайд 5Теорема
Средняя линия треугольника, соединяющая середины двух данных сторон,
параллельна третьей стороне и равна её половине
т.е.:
ED ║АB
ED = ½ АB
A
С
В
Е
D
Слайд 14
Трапеция – это четырехугольник ,
у которой только две противолежащие
стороны параллельны.
BC || AD - основания
AB łł CD – боковые
стороны
Слайд 15Равнобедренная трапеция
Определение:
Трапеция, у которой боковые стороны равны, называется равнобедренной.
AB=CD
ABCD -
равнобедренная трапеция
Слайд 16Прямоугольная трапеция
Определение:
Трапеция, у которой один из углов прямой, называется прямоугольной.
ABCD
- прямоугольная трапеция
Слайд 17Средняя линия трапеции.
Определение: Средней линией трапеции называется отрезок, соединяющий
середины её боковых сторон.
MN – средняя линия
трапеции ABCD
Слайд 18Теорема о средней линии трапеции
Средняя линия трапеции параллельна её
основаниям и равна их полусумме.
т.е.:МN║ВС║АD
МN=½(ВС+АD)
Слайд 19
Дано:
АВСD-трапеция QP – средняя линия Доказать:Доказательство. Проведем через вершину В и середину Р боковой стороны CD прямую. Она пересекает прямую AD в некоторой точке Е
Треугольники РВС и PED равны по второму признаку равенства треугольников. У них CP=DP по построению, углы при вершине Р равны как вертикальные, а углы РСВ и PDE равны как внутренние накрест лежащие при параллельных прямых ВС и AD и секущей CD. Из равенства треугольников следует равенство сторон: РВ=РЕ, BC=ED.
Значит, средняя линия PQ трапеции является средней линией треугольника ABE. По свойству средней линии треугольника PQ II AD и отрезок PQ= ½ (AD+BC)
Слайд 25Решить задачу № 3
Дано: MN - средняя линия ΔАВС; АС
=100мм
M1N1 - средняя линия ΔMВN
Найти: M1N1
A
B
С
M
N
M₁
N₁
?
Слайд 26Решить задачу № 4:
Дано: АВСD- прямоугольная трапеция; ВС=3
СD=4; MN
- средняя линия ΔАВD
Найти: MN
M
N
А
С
D
В
?
Слайд 27Решить задачу № 5
Дано: ΔАВС подобен ΔВDК; ВС=10; ВD=15; DК=9;
MN - средняя линия ΔАВС
Найти: MN
M
N
А
В
С
D
К
?
Слайд 28Решить задачу № 6
Дано: АВСD-трапеция;ВD =25; СD =10; АВ=12
MN-средняя
линия ΔАВD
Найти: MN
A
В
С
D
M
N
?
Слайд 29Решить задачу № 7
Дано: АВСD-прямоугольник; ВС=17см;
О- точка пересечения диагоналей;
ОК┴ВС; ОК=4см
Найти: PАВСD
В
А
С
D
K
O
Слайд 30Задача № 8.
Дан прямоугольный треугольник АВС. Гипотенуза АВ равна 50
см. Прямая АD делит сторону СВ пополам. МN – средняя
линия треугольника АВD и равна 10 см. Найти катет АС.
Слайд 31
Решение.
1) т.к. МN – средняя линия треугольника АВD, то
ВD= 2·10=20(см).
2) т.к. ВD=DС, то
ВС=2·20=40(см).3) т.к. ΔАВС-
прямоугольный, то
по т. Пифагора имеем: а²= с²-в², т.е.
АС²=50²- 40²=2500-1600=900
Тогда АС=30(см)
Ответ: АС=30(см)
A
С
В
M
D
N
?
10
50
Слайд 33Самостоятельная работа
Дано: АВСD – трапеция; MN=8
S АВСD = 56; MN- средняя линия
Найти: высоту
A
M
С
N
D
К
В
