Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Различные способы решения квадратных уравнений
Содержание
- 1. Различные способы решения квадратных уравнений
- 2. У.У.Сойер:"Человеку изучающему алгебру, часто полезно решить
- 3. Способырешенияквадратногоуравнения Х2+4x-5=0
- 4. 1СПОСОБ. Разложение левой части уравнения на множители.Решим
- 5. 2СПОСОБ. Метод выделения полного квадрата.Решим уравнение х2
- 6. 3СПОСОБ.Решение квадратных уравнений по формуле.1)Уравнение ах2 +
- 7. 2)Уравнение ax2+2kx+c=0, a=0 имеет корни
- 8. 4СПОСОБ.Решение уравнений с использованием теоремы Виета.х2
- 9. 5СПОСОБ.Решение уравнений способом «переброски».ах2 + bх +
- 10. Применим этот способ к нашему уравнению:х2 +
- 11. Рассмотрим другое уравнение2x2+3x+1=0;4x2+6x+2=0;y2+3y+2=0;D=9-4 12=1x1=-1, x2=-1/2Ответ:-1;-1/2
- 12. 6СПОСОБ.Свойства коэффициентов квадратного уравнения. ах2 + bх
- 13. Применим этот способ к нашему уравнению:х2 +
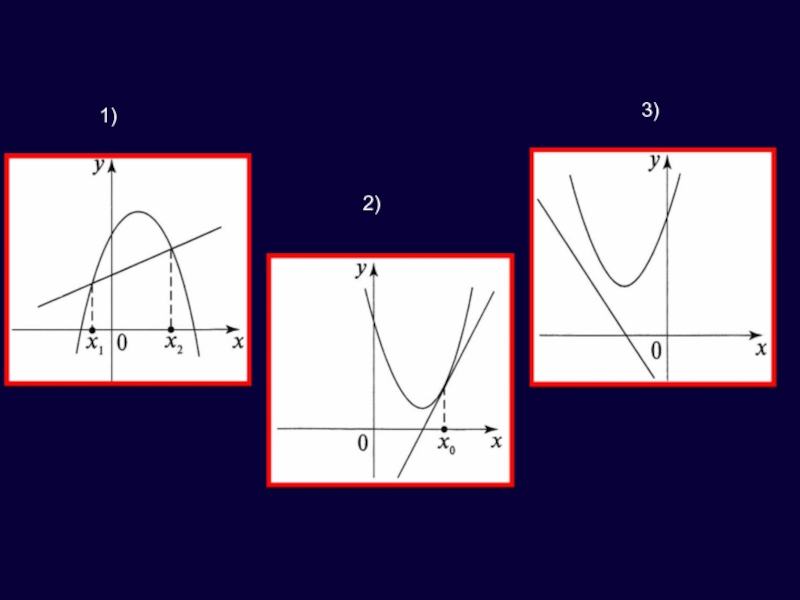
- 14. 7СПОСОБ: Графическое решение квадратного уравнения. Если в
- 15. 1)Если прямая и парабола пересекаются в двух
- 16. 1)2)3)
- 17. Решим графически уравнение х2
- 18. 8СПОСОБ.Решение квадратных уравнений с помощью циркуля и
- 19. Решим уравнение х2 +
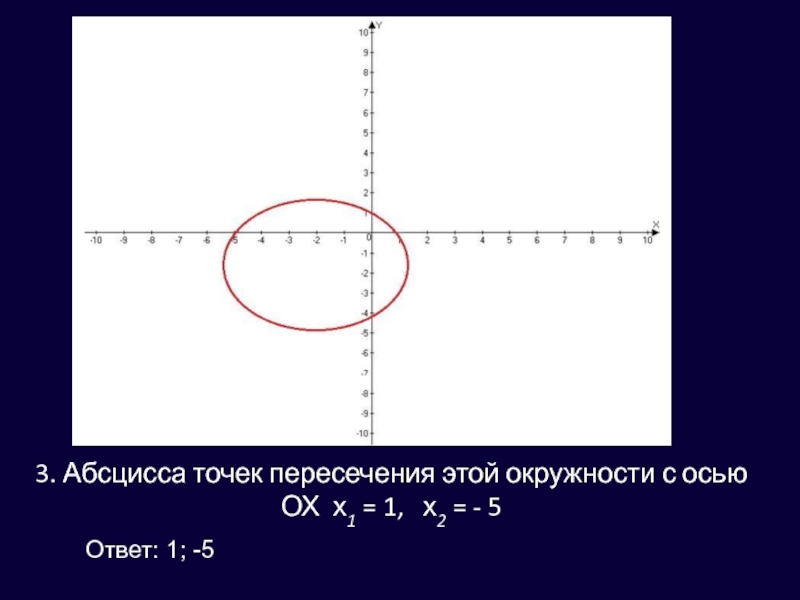
- 20. 3. Абсцисса точек пересечения этой окружности с
- 21. 9СПОСОБ: Решение квадратных уравнений с помощью номограммы.
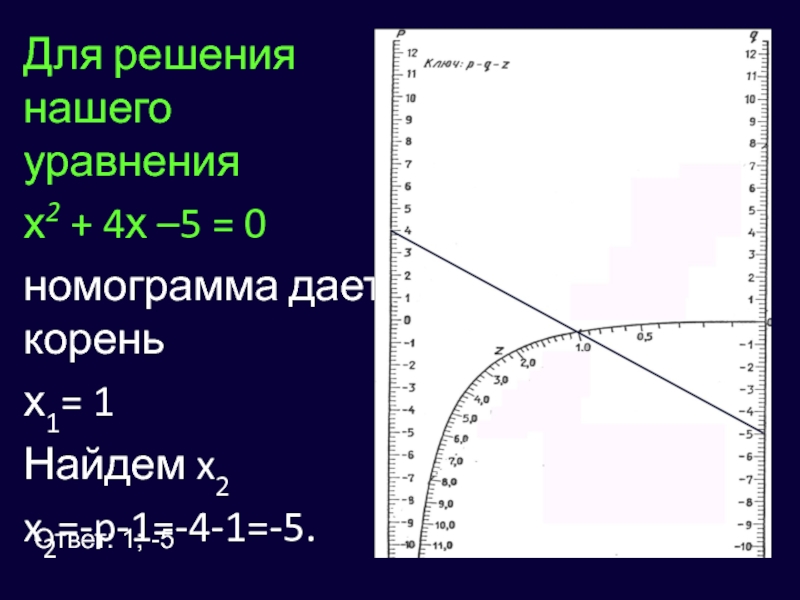
- 22. Для решения нашего уравнениях2 + 4х –5 = 0номограмма дает кореньх1= 1Найдем x2x2=-p-1=-4-1=-5.Ответ: 1; -5
- 23. 10СПОСОБ.Геометрический способ решения квадратных уравнений.Решим уравнение х2
- 24. Применим этот способ к нашему уравнению11 СПОСОБ.
- 25. 12СПОСОБ.Формула Герона для решения квадратных уравненийax2 + bx = c
- 26. Применим этот способ к нашему уравнению
- 27. 13СПОСОБ.Альтернативный метод решения квадратных уравнений.(А.В.Борисов, канд.техн.наук, Л.Н.Королевич)Рассмотрим
- 28. Для этого необходимо:1. определить величину угла θ
- 29. Применим этот способ к нашему уравнениюx2+4x-5=0.Промежуточные величины определяются по формулам
- 30. Тогда Ответ: 1; -5Но как мы видим этот способ нельзя назвать самым удачным.
- 31. заключение Великий Д.Пойа говорил: «Если вы хотите
- 32. ЛитератураМатериалы сайта http://www.nbuv.gov.ua/portal/natural/EiS/2010_1/12_Korolevich.pdfМатематическая энциклопедия: Гл. ред. И.М.
- 33. Спасибо за внимание
- 34. Скачать презентанцию
Слайды и текст этой презентации
Слайд 41СПОСОБ. Разложение левой части уравнения на множители.
Решим уравнение х2 +
4x – 5 = 0.
Разложим левую часть на множители:
x2-x+5
х – 5 = 0 ;( х2 – х ) + ( 5 х – 5) = 0;
х ( х – 1 ) + 5( х – 1 ) = 0;
( х – 1 )( х +5 ) = 0
Тогда х1 = 1 и х2 = - 5
Ответ: 1; -5
Слайд 52СПОСОБ. Метод выделения полного квадрата.
Решим уравнение х2 + 4х –
5= 0.
х2 +4x=5;
х2 + 22х=5;
х2 + 22 х +4=5+4;
( х
+ 2 )2 =9.Следовательно,
х + 2= 3 или х +2= - 3
х1 = 1 х2 = -5
Ответ: 1; -5
Слайд 63СПОСОБ.Решение квадратных уравнений по формуле.
1)Уравнение ах2 + bх + с
= 0, а ≠ 0, имеет корни
Решим уравнение х2
+ 4х – 5= 0, а ≠ 0.x1=-4+ 16-41(-5)= -4+ 36 = -4+6 =1
21 2 2
x1= -4- 16-4•1(-5)= -4- 36 = -4-6 = -5
21 2 2
Ответ: 1; -5
Слайд 72)Уравнение ax2+2kx+c=0, a=0 имеет корни
x1,2=
Решим уравнение x2+4x-5=0,a>0;k=2.
Ответ: 1; -5
Слайд 8 4СПОСОБ.Решение уравнений с использованием теоремы Виета.
х2 + px +
q = 0.
Его корни удовлетворяют теореме Виета, которая при
а =1 имеет вид x1 x2 = q,
x1 + x2 = - p.
Применим этот способ к нашему уравнению
x2+4x-5=0.
x1+x2=-4, x1=1,
x1•x2=-5; x2=-5.
Ответ: 1; -5
Слайд 95СПОСОБ.Решение уравнений способом «переброски».
ах2 + bх + с = 0,
где а ≠ 0.
Умножая обе его части на а, получаем
уравнениеа2х2+ аbх + ас = 0.
Пусть ах = у, откуда х = у/а; тогда приходим к уравнению
у2 + by + ас = 0,
равносильно данному. Его корни у1 и у2 найдем с помощью теоремы Виета.
Окончательно получаем х1 = у1/а и х2= у2/а.
Слайд 10Применим этот способ к нашему уравнению:
х2 + 4х –5= 0
, ах = у, а=1.
у2 + 4у – 5= 0
По т.Виета у1 = 1,у2 = -5.
Значит , x1=1,x2=-5.
Ответ: 1; -5
Слайд 11
Рассмотрим другое уравнение
2x2+3x+1=0;
4x2+6x+2=0;
y2+3y+2=0;
D=9-4 12=1
x1=-1, x2=-1/2
Ответ:-1;-1/2
Слайд 126СПОСОБ.Свойства коэффициентов квадратного уравнения.
ах2 + bх + с =
0, a=0.
1)Если a+b+c=0, то x1=1,x2=c/a.
2) Если a-b+c=0, то x1=-1,x2=-c/a.
Слайд 13Применим этот способ к нашему уравнению:
х2 + 4х -5 =
0.
а + b + с = 0, 1 + 4
– 5= 0 х1 = 1,
х2 = с/а = -5/1= -5.
Ответ: 1; -5
Слайд 147СПОСОБ: Графическое решение квадратного уравнения.
Если в уравнении х2 +
рх + q = 0 перенести второй и третий члены
в правую часть, то получимх2 = – рх – q.
Построим
графики зависимостей
у = х2 и у = – рх – q.
(рис.1)
Слайд 151)Если прямая и парабола пересекаются в двух точках, то уравнение
имеет два решения.
2) Если прямая и парабола пересекаются в одной
точке, то уравнение имеет одно решение.3)Если прямая и парабола не пересекаются, то уравнение не имеет решений.
Слайд 17
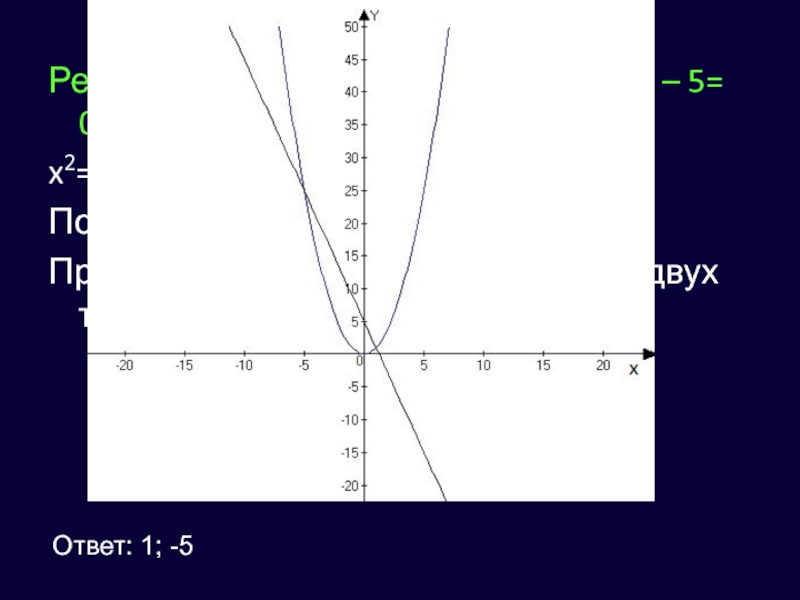
Решим графически уравнение х2 + 4х – 5= 0.
x2=-4x+5
Построим y=x2
и y=-4x+5
Прямая и парабола пересекаются в двух точках абсциссами х1
= 1, х2 = -5Ответ: 1; -5
Слайд 188СПОСОБ.Решение квадратных уравнений с помощью циркуля и линейки.
1)Построим точки S
( -b/2a ; (а+с) /2a )(центр окружности) и А (0
; 1).2)Проведем окружность с радиусом SA;
3)Абсциссы точек пересечения этой окружности с осью ОХ является корнями исходного квадратного уравнения.
Слайд 19
Решим уравнение х2 + 4х – 5= 0.
1. Определим координаты
точки центра окружности по формулам:
S ( - b/2a ;(а+с )/2a
)х = - b/2a = -4/2 = -2
у = (а+с) /2a =(1+(-5)):2 = - 2
S ( - 2 ; - 2) и А ( 0 ; 1 ).
2. Проведем окружность с R = SA , где А ( 0 ; 1 ).
R=
Слайд 219СПОСОБ: Решение квадратных уравнений с помощью номограммы.
Номограмма даёт значения
положительных корней уравнения z2+pz+q=0
Если это уравнение имеет корни
разных знаков , то , найдя по номограмме положительный корень, отрицательный находят ,вычитая положительный из -p .В случае ,когда оба корня отрицательны, берутz=-t и находят по номограмме два положительных корня t1 и t2 уравнения t2-pt+q=0,а затем z1=-t1, z2=-t2.Если коэффициенты p и q выходят за пределы шкал, выполняют подстановку z=kt и решают посредством номограммы уравнение
Уравнение, где k берется с таким расчётом, чтобы имели место неравенства:
Слайд 22Для решения нашего уравнения
х2 + 4х –5 = 0
номограмма дает
корень
х1= 1
Найдем x2
x2=-p-1=-4-1=-5.
Ответ: 1; -5
Слайд 2310СПОСОБ.Геометрический способ решения квадратных уравнений.
Решим уравнение х2 + 4х= 5.
Sпрям
= 1 х
Sкв = 1 1= 1
SABCD = х2
+ 4 Sпрям + 4 Sкв SABCD = х2 + 4 1х + 4 1= х2 + 4х + 4
заменяя х2 + 4х числом 5, получим, что S = 5+ 4 =9.
Имеем (x+2)2=9
АВ = 3
х = 3 – 1 –1= 1.
Ответ: 1; -5
A
B
C
D
Слайд 24
Применим этот способ к нашему уравнению
11 СПОСОБ. Для нахождения корней
приведённого квадратного уравнения х2 +
px + q = 0 полезно воспользоваться формулойх2 + 4х= 5.
Ответ: 1; -5
Слайд 2713СПОСОБ.Альтернативный метод решения квадратных уравнений.
(А.В.Борисов, канд.техн.наук, Л.Н.Королевич)
Рассмотрим новый метод решения
квадрат-
ных уравнений, который применим к приведенным квадратным
уравнениям
Обозначения
atr, btr –
длины катетов прямоугольного тре-угольника (далее просто катеты);
ctr – длина гипотенузы прямоугольного тре-
угольника (далее просто гипотенуза);
αtr, βtr – острые углы против катетов atr и btr
соответственно;
φtr – один из острых углов прямоугольного
треугольника (atr или btr );
mtr – длина медианы, опущенной на гипоте-
нузу (далее просто медиана);
htr – длина высоты, опущенной на гипотенузу
(далее просто высота);
θtr – угол между медианой и высотой;
?tr – угол между медианой и гипотенузой.
Слайд 28Для этого необходимо:
1. определить величину угла θ (соответст-
вует углу φtr
), как
2. определить величину угла φ (соответст-
вует углу φtr ),
какили как
3. определить первый корень:
4. определить второй корень:
или
Слайд 29 Применим этот способ к нашему уравнению
x2+4x-5=0.
Промежуточные величины определяются по формулам
Слайд 31заключение
Великий Д.Пойа говорил: «Если вы хотите научиться плавать, то
смело входите в воду, а если хотите научиться решать задачи,
то решайте их». Мне хочется продолжить, если хотите научиться решать уравнения, то решайте их и не просто решайте, а решайте с вдохновением самым удачным и подходящим способом. Ведь Г.Лейбниц заметил: «Первое условие, которое надлежит выполнять в математике, - это быть точным, второе - быть ясным и, насколько можно, простым». Ваше решение должно приносить Вам удовлетворение!Слайд 32Литература
Материалы сайта http://www.nbuv.gov.ua/portal/natural/EiS/2010_1/12_Korolevich.pdf
Математическая энциклопедия: Гл. ред. И.М. Виноградов-М., «Советская Энциклопедия»,1979.
Справочник
по математике.-3-е изд., перераб./ Гусев В.А., Мордкович А.Г.-М.: Просвещение,1995.
Газета «Математика»
№24 июнь 1995 г.Журнал «Квант» №2 1996 г.
В.В. Ткачук «Математика абитуриенту» 2001 г.
«Энциклопедия элементарной математики» Книга вторая. Алгебра, 1951 г.
Л.Ф.Пичурин «За страницами учебника алгебры"