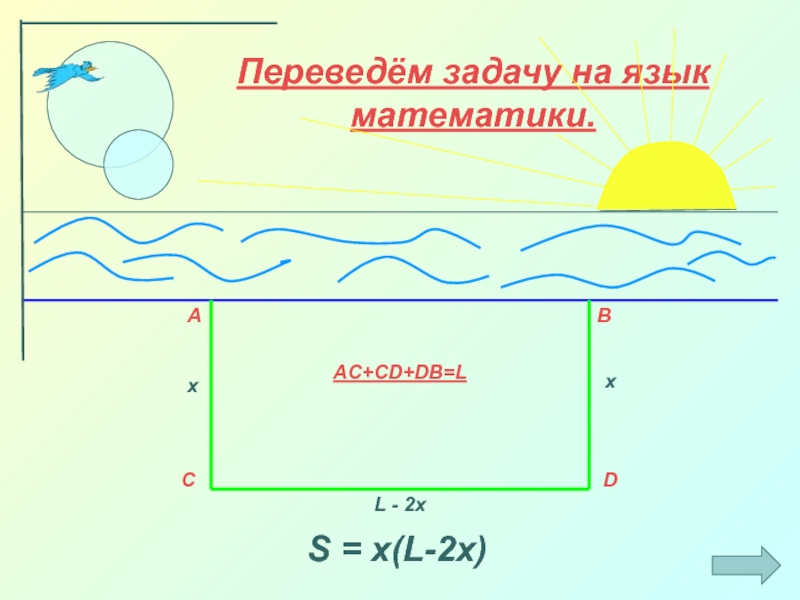
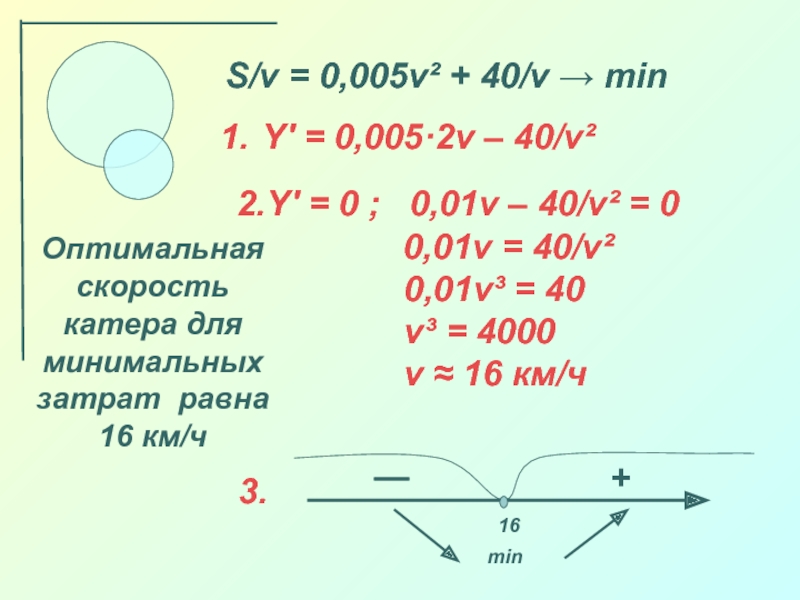
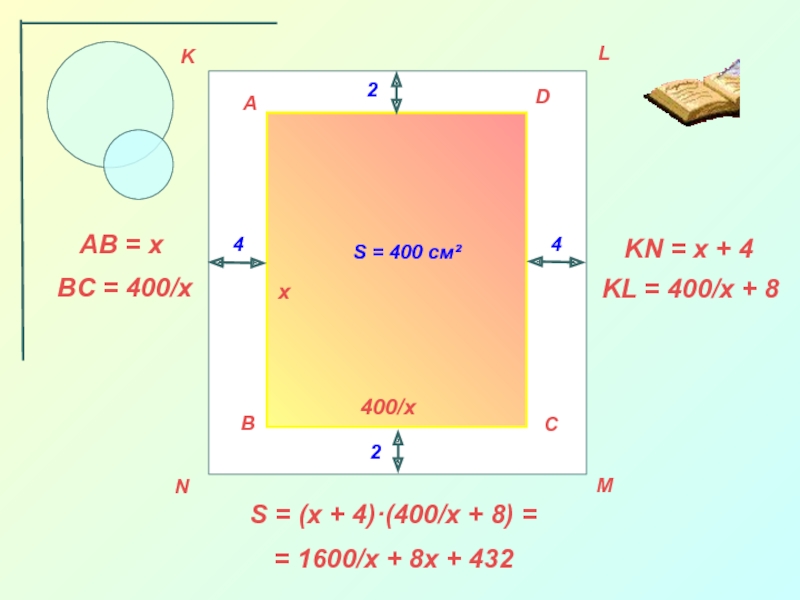
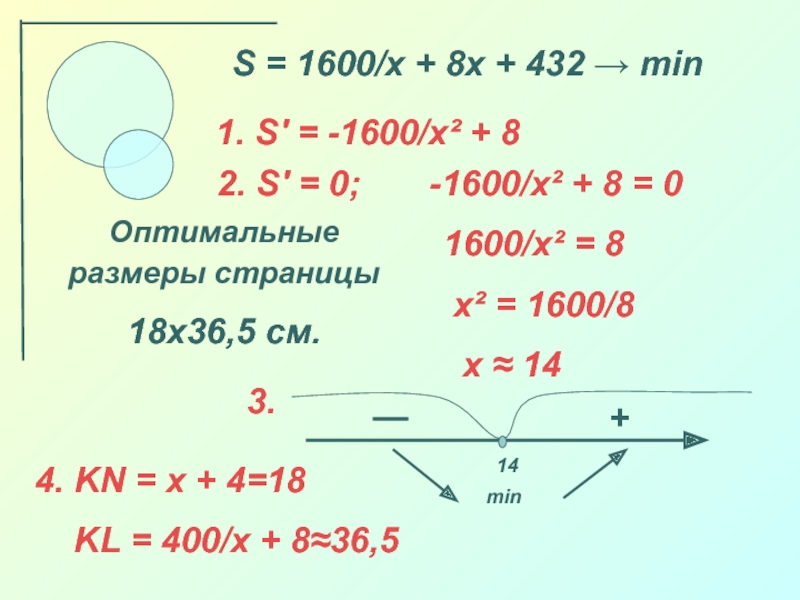
частей: стоимости топлива, пропорциональной кубу скорости баржи, и стоимости амортизации
баржи ( зарплата команды, стоимость оборудования и т. д.). Общая стоимость содержания баржи за час выражается формулой: S = av³ + b, где v- скорость судна в км/ч, a и b – коэффициенты, заданные для каждого судна (для нашего а=0,005, b=40).
Ясно, что расходы на топливо будут тем больше, чем быстрее движется корабль, остальные расходы от скорости не зависят.
Казалось бы, чем медленнее движется корабль, тем дешевле его эксплуатация. Так ли это?

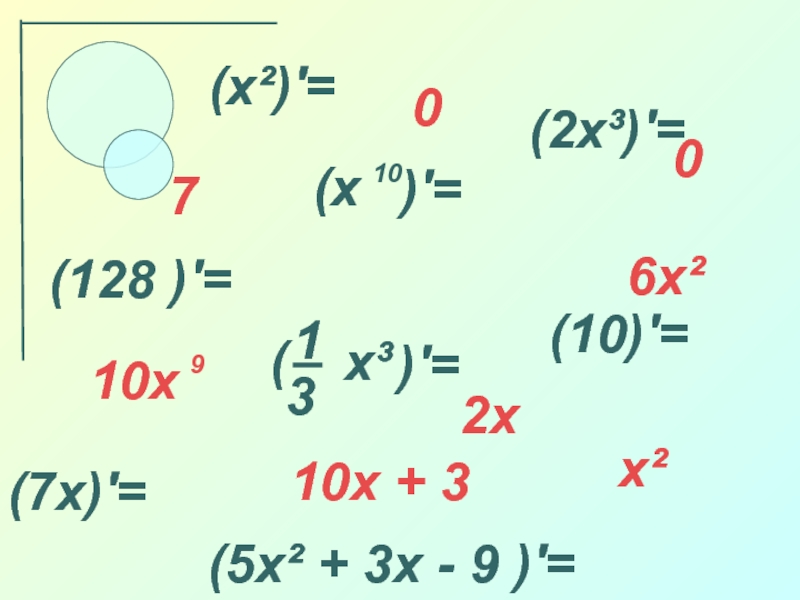

![Нахождение наибольшего и наименьшего значений непрерывной функции на промежутке. Выполните задание:Найти промежутки возрастания и убывания функции.Найти экстремумы функции.Найти наибольшее и Выполните задание:Найти промежутки возрастания и убывания функции.Найти экстремумы функции.Найти наибольшее и наименьшее значение функции на отрезке [-1;2]Y](/img/thumbs/cfd34c7af7b644e18b34697966e0aaf4-800x.jpg)