Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация к уроку геометрии по теме "Сумма углов треугольника" с элементами исследовательской работы
Содержание
- 1. Презентация к уроку геометрии по теме "Сумма углов треугольника" с элементами исследовательской работы
- 2. ТреугольникВАСТреугольник – самая простая замкнутая прямолинейная фигура,
- 3. Архитектура
- 4. Витражи
- 5. П а р к е т
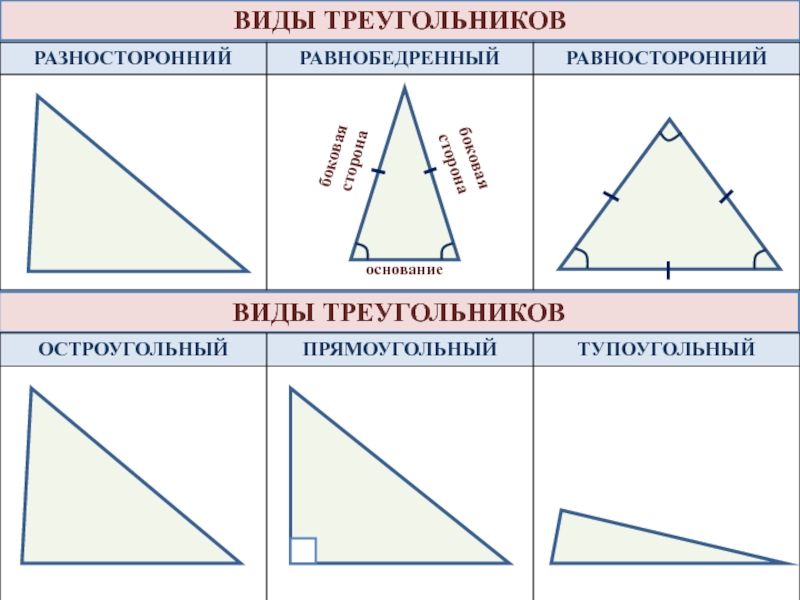
- 6. ВИДЫ ТРЕУГОЛЬНИКОВВИДЫ ТРЕУГОЛЬНИКОВ
- 7. Тест «Признаки равенства треугольников»1) Какой элемент треугольника
- 8. Тест «Признаки равенства треугольников»2) Можно ли утверждать,
- 9. Тест «Признаки равенства треугольников»3) В треугольниках АВС
- 10. Найдите неизвестный угол
- 11. Прямые а и b параллельны, с - секущаяНайдите неизвестный угол аbс
- 12. Прямые а и b параллельны, с - секущаяНайдите неизвестный угол аbс
- 13. Прямые а и b параллельны, с - секущаяНайдите неизвестный угол аbс
- 14. Найдите углы треугольника АВС, m АСm213
- 15. Сумма углов треугольникаВАС
- 16. Слайд 16
- 17. Исследование 1:С помощью «отрывания» углов треугольника можно показать, что сумма его углов равна 180°.
- 18. План исследования:1. Оторвите любые два угла треугольника.2.
- 19. Исследование 2:
- 20. Вывод: мы опытным путём показали справедливость
- 21. Теорема о сумме углов треугольникаАВС
- 22. Пифагор Самосский – древнегреческий философ, математик(580 –
- 23. Слайд 23
- 24. Групповая работа.Доказать теорему о сумме углов треугольника
- 25. Задача 1.?МNK
- 26. Задача 2.АВС?
- 27. Задача 3.?ВАС?
- 28. Задача 4.?РKS?
- 29. Задача 5.АВС??
- 30. Задача 6.CDF???
- 31. Самостоятельная работа
- 32. Самостоятельная работаОтветы:Вариант 1Вариант 2
- 33. Слайд 33
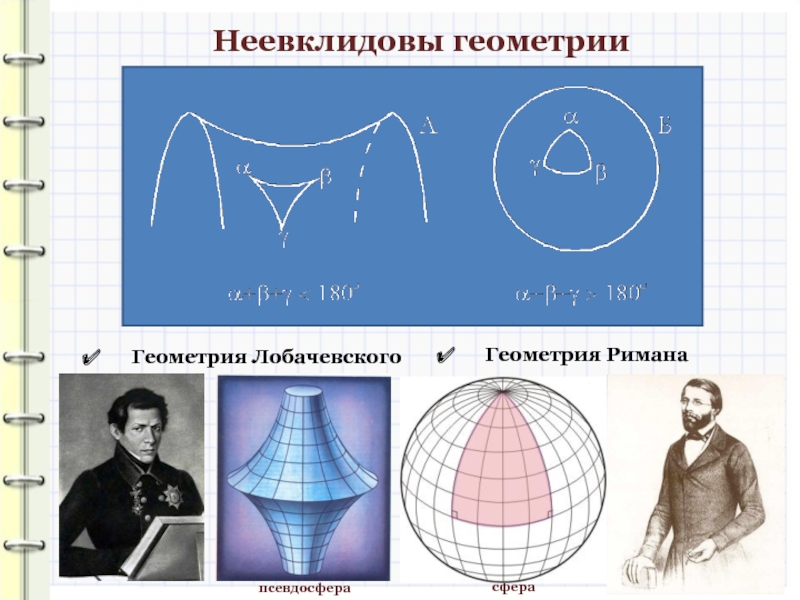
- 34. Неевклидовы геометрииГеометрия ЛобачевскогоГеометрия Риманапсевдосферасфера
- 35. Оценим свою работу на уроке
- 36. Домашнее задание§1, п. 31; № 223 (а,
- 37. Скачать презентанцию
ТреугольникВАСТреугольник – самая простая замкнутая прямолинейная фигура, одна из первых, свойства которой человек узнал еще в глубокой древности. Изображения треугольников и задачи на треугольники встречаются в папирусах, в старинных индийских книгах.
Слайды и текст этой презентации
Слайд 7Тест «Признаки равенства треугольников»
1) Какой элемент треугольника АВС необходимо
задать,
чтобы треугольники АВС и DEF были
равны по I признаку
равенства треугольников? а) ∠С = 50°; б) АС = 7 см; в) ∠В = 50°.
А
В
С
5,5 см
35°
D
35°
F
50°
7 см
5,5 см
E
Слайд 8Тест «Признаки равенства треугольников»
2) Можно ли утверждать, что треугольники,
изображенные
на рисунке, равны?
а) да;
б) нет.
Слайд 9Тест «Признаки равенства треугольников»
3) В треугольниках АВС и DEF АВ
= DE, ВC = EF.
Какое ещё условие должно быть
выполнено, чтобы треугольники были равны?
а) ∠A = ∠D; б) ∠С = ∠F; в) ∠В = ∠E; г) АС=DF.
A
В
С
D
E
F
Слайд 16
Эпиграф
Легче остановить Солнце,
легче двинуть Землю,
чем изменить сумму
углов треугольника...
Вениамин Фёдорович Каган
(российский и советский математик, доктор физико-математических наук, профессор МГУ)
(1869 - 1953)
Слайд 17Исследование 1:
С помощью «отрывания» углов треугольника можно показать, что
сумма его углов равна 180°.
Слайд 18План
исследования:
1. Оторвите любые два угла треугольника.
2. Приложите оторванные углы
к третьему.
3. Ответьте на вопросы:
Какой угол образовали
углы треугольника? Чему равна его градусная мера?
4. Сделайте вывод.
Слайд 20 Вывод: мы опытным путём показали справедливость утверждения о том,
что сумма углов треугольника равна 180° .
Достаточно ли этого
для доказательства утверждения?
Слайд 22Пифагор Самосский – древнегреческий философ, математик
(580 – 500 гг. до
н. э.)
Доказательство теоремы о сумме углов треугольника, изложенное в
современных учебниках, было открыто пифагорейцами(V в. до н. э.).
Слайд 24
Групповая работа.
Доказать теорему о сумме углов треугольника по готовым чертежам.
А
В
С
1
3
2
4
5
M
N
I группа
II группа
А
В
С
Е
1
2
3
4
5
D
III группа
Смотрите рис. II группы. При доказательстве использовать
свойство односторонних углов при пересечении двух параллельных прямых секущей 
Слайд 33
Эпиграф
Легче остановить Солнце,
легче двинуть Землю,
чем изменить сумму
углов треугольника...
Вениамин Фёдорович Каган
(российский и советский математик, доктор физико-математических наук, профессор МГУ)
(1869 - 1953)
Слайд 36Домашнее задание
§1, п. 31;
№ 223 (а, б) (базовый уровень)
№
225, выучить одно из рассмотренных доказательств теоремы (средний уровень);
№ 228,
найти и выучить с помощью дополнительных источников информации ещё одно доказательство теоремы (повышенный уровень)
