Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация к уроку по геометрии (10 класс) на тему "Задачи на построение сечений"
Содержание
- 1. Презентация к уроку по геометрии (10 класс) на тему "Задачи на построение сечений"
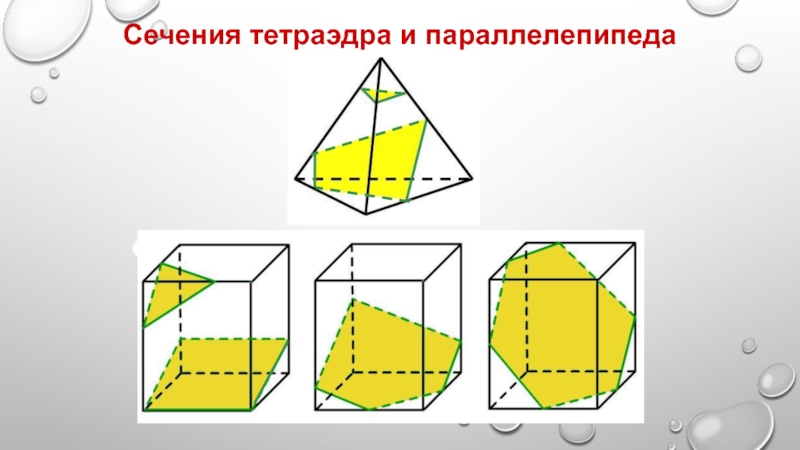
- 2. Сечения тетраэдра и параллелепипеда
- 3. Секущей плоскостью тетраэдра называется любая плоскость, по
- 4. Т.к. тетраэдр имеет четыре грани, то его сечениями могут быть только треугольники и четырёхугольники.
- 5. Параллелепипед имеет шесть граней. Его сечениями могут быть треугольники (а), четырёхугольники, пятиугольники (б) и шестиугольники (в).а)б)в)
- 6. Задача1. На рёбрах AB, BD и CD
- 7. Решение. Построим сначала прямую, по которой плоскость
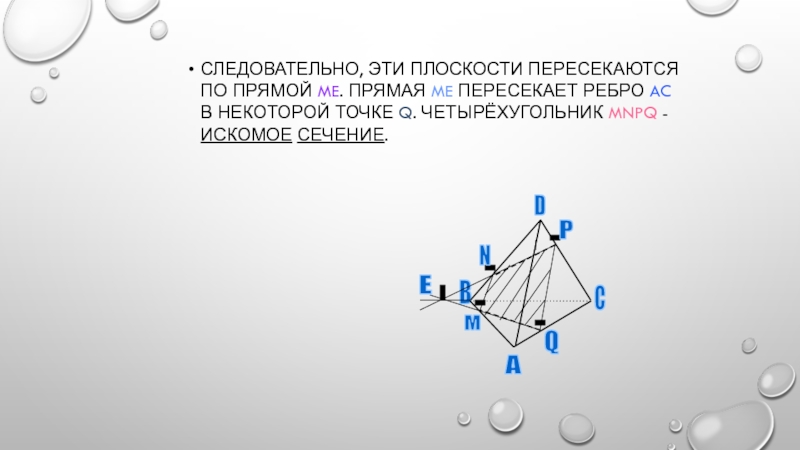
- 8. Следовательно, эти плоскости пересекаются по прямой ME.
- 9. Задача 2 На рёбрах параллелепипеда даны три
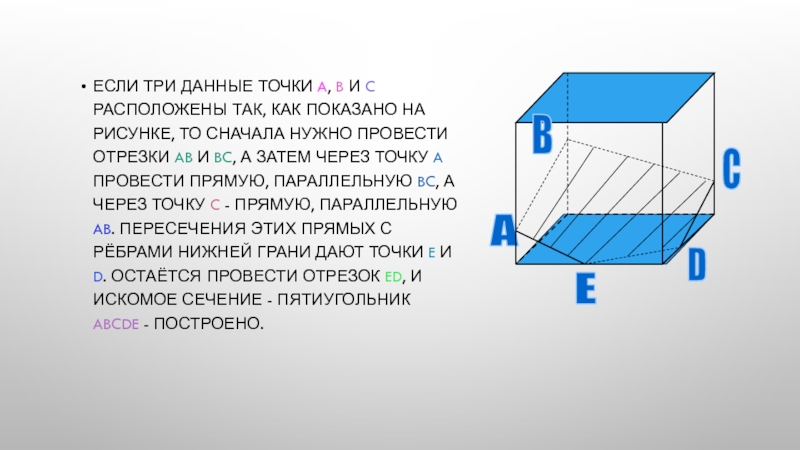
- 10. Если три данные точки A, B и
- 11. Более трудный случай, когда данные точки A,
- 12. Эта прямая пересекается с рёбрами нижнего основания
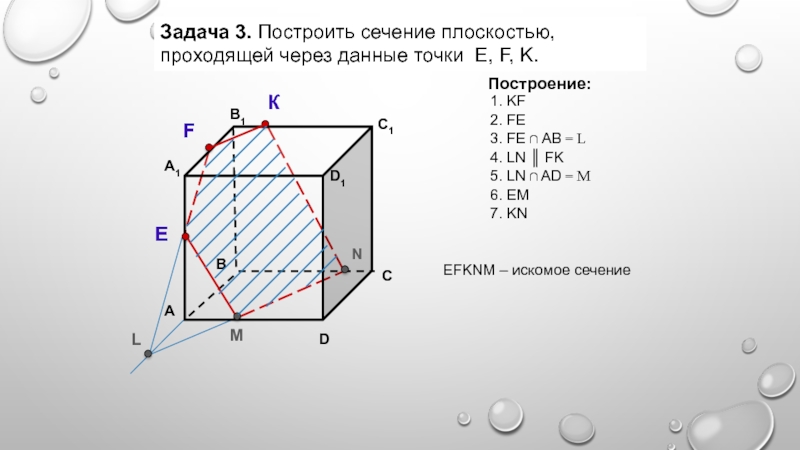
- 13. Задача 3. Построить сечение плоскостью, проходящей через
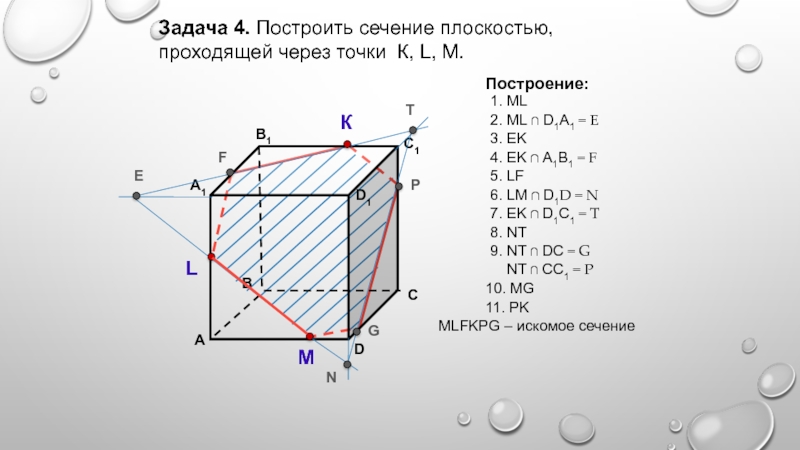
- 14. Задача 4. Построить сечение плоскостью, проходящей через
- 15. Задача 5Построить сечение четырехугольной пирамиды QWBCE плоскостью,
- 16. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Задачи на построение сечений
Выполнила Жеревчук Алина
учащаяся 11 Б класса
учитель:
Фаязова оксана викторовна
Слайд 3Секущей плоскостью тетраэдра называется любая плоскость, по обе стороны от
которой имеются точки данного тетраэдра (параллелепипеда). Секущая плоскость пересекает грани
тетраэдра по отрезкам.Многоугольник, сторонами которого являются эти отрезки, называется сечением тетраэдра (параллелепипеда).
Далее
Слайд 4Т.к. тетраэдр имеет четыре грани, то его сечениями могут быть
только треугольники и четырёхугольники.
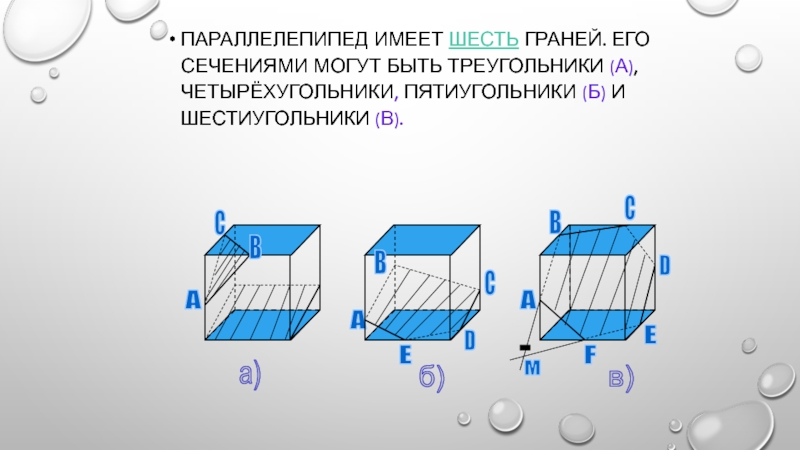
Слайд 5Параллелепипед имеет шесть граней. Его сечениями могут быть треугольники (а),
четырёхугольники, пятиугольники (б) и шестиугольники (в).
а)
б)
в)
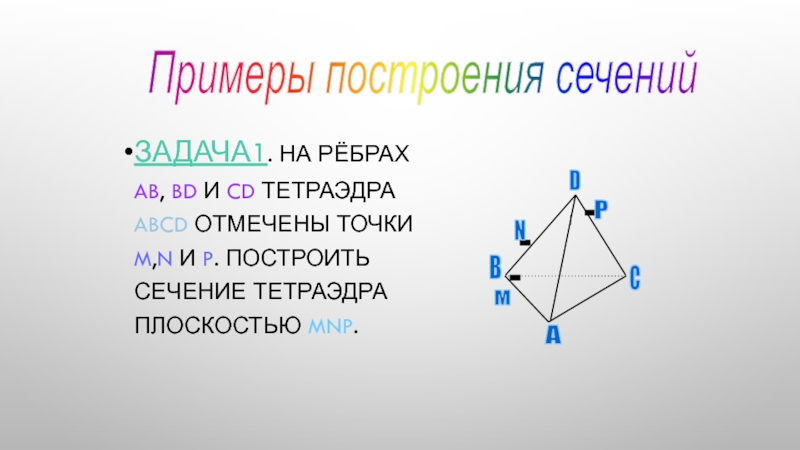
Слайд 6Задача1. На рёбрах AB, BD и CD тетраэдра ABCD отмечены
точки M,N и P. Построить сечение тетраэдра плоскостью MNP.
Примеры построения
сеченийСлайд 7Решение.
Построим сначала прямую, по которой плоскость MNP пересекается с
плоскостью грани ABC. Точка М является общей точкой этих плоскостей.
Для построения ещё одной общей точки продолжим отрезки NP и BC до их пересечения в точке Е, которая и будет второй общей точкой плоскостей MNP и ABC.Слайд 8Следовательно, эти плоскости пересекаются по прямой ME. Прямая ME пересекает
ребро AC в некоторой точке Q. Четырёхугольник MNPQ - искомое
сечение.Слайд 9Задача 2 На рёбрах параллелепипеда даны три точки A, B
и C. Построить сечение параллелепипеда плоскостью ABC.
Решение. Построение искомого сечения
зависит от того, на каких рёбрах параллелепипеда лежат точки A, B и C. Когда эти точки лежат на рёбрах, выходящих из одной вершины, нужно провести отрезки AB, BC и CA, и получится искомое сечение - треугольник ABC.Слайд 10Если три данные точки A, B и C расположены так,
как показано на рисунке, то сначала нужно провести отрезки AB
и BC, а затем через точку A провести прямую, параллельную BC, а через точку C - прямую, параллельную AB. Пересечения этих прямых с рёбрами нижней грани дают точки E и D. Остаётся провести отрезок ED, и искомое сечение - пятиугольник ABCDE - построено.Слайд 11Более трудный случай, когда данные точки A, B C расположены
так, как показано на рисунке. В этом случае сначала построим
прямую, по которой секущая плоскость пересекается с плоскостью нижнего основания.Для этого проведём прямую AB, до пересечения с этой прямой в точке M. Далее через точку M проведём прямую, параллельную прямой BC. Это и есть прямая, по которой секущая плоскость пересекается с плоскостью нижнего основания.
Слайд 12Эта прямая пересекается с рёбрами нижнего основания в точках E
и F. Затем через точку E проведём прямую, параллельную прямой
AB, и получим точку D. Проводим отрезки AF и CD, и искомое сечение - шестиугольник ABCDEF - построено.Слайд 13Задача 3. Построить сечение плоскостью, проходящей через данные точки Е,
F, K.
Построение:
1. KF
2. FE
3. FE ∩ АB = L
EFKNM –
искомое сечение4. LN ║ FK
6. EM
5. LN ∩ AD = M
7. KN
К
L
М
F
E
N
Слайд 14Задача 4. Построить сечение плоскостью, проходящей через точки К, L,
М.
К
L
М
Построение:
1. ML
2. ML ∩ D1А1 = E
3. EK
МLFKPG – искомое
сечениеF
E
N
P
G
T
4. EK ∩ А1B1 = F
6. LM ∩ D1D = N
5. LF
7. ЕK ∩ D1C1 = T
8. NT
9. NT ∩ DC = G
NT ∩ CC1 = P
10. MG
11. PK
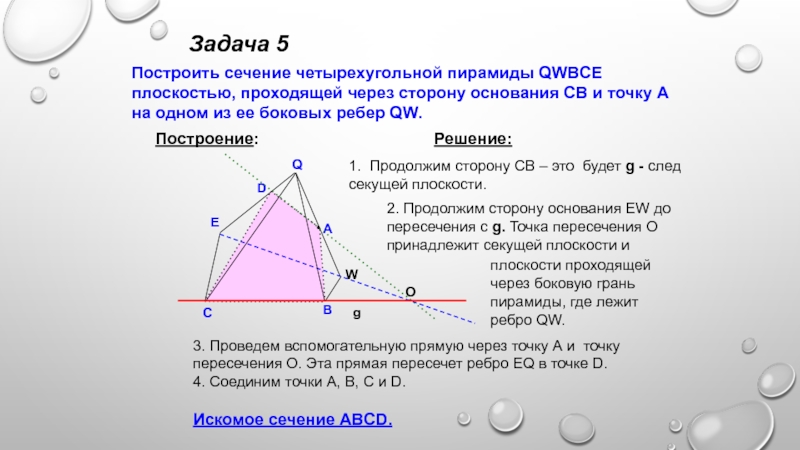
Слайд 15Задача 5
Построить сечение четырехугольной пирамиды QWBCE плоскостью, проходящей через сторону
основания CB и точку А на одном из ее боковых
ребер QW.Построение:
Решение:
g
A
B
C
D
Q
W
E
О
2. Продолжим сторону основания EW до пересечения с g. Точка пересечения О принадлежит секущей плоскости и
3. Проведем вспомогательную прямую через точку А и точку пересечения О. Эта прямая пересечет ребро EQ в точке D.
4. Соединим точки A, B, C и D.
Искомое сечение ABCD.
1. Продолжим сторону CB – это будет g - след секущей плоскости.
плоскости проходящей через боковую грань пирамиды, где лежит ребро QW.