Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теорема Менелая и ее применение при решении задач (подготовка к ЕГЭ)
Содержание
- 1. Теорема Менелая и ее применение при решении задач (подготовка к ЕГЭ)
- 2. СодержаниеТеоретические факты: а) пропорциональные отрезки в
- 3. Теоретические фактыТеорема Фалеса Параллельные
- 4. Теоремы об отношении площадей треугольников2. Пусть ∆АВС
- 5. Задача.(Р.К.Гордин.Математика.ЕГЭ-2014.ЗадачаС4.№6.3)
- 6. Предложенный вариант решения задачи –
- 7. Теорема Менелая Если на сторонах ВС,
- 8. Доказательство Проведем СК //АВ, тогда ∆СКВ´ ~
- 9. Задача.(Р.К.Гордин.Математика.ЕГЭ-2014.ЗадачаС4.№6.3)
- 10. Найти: Ответ: Задача. (Р.К.Гордин. Математика. ЕГЭ-2014.
- 11. Задача. (Р. К. Гордин. Математика. ЕГЭ-2014.
- 12. Задача.( Математика ЕГЭ-2014. Типовые тестовые задания. 30
- 13. Задача. (Сайт А.А.Ларина. Тренировочный вариант №67. от
- 14. Задача. (Сайт А.А.Ларина. Тренировочный вариант №67. от
- 15. Заключение Решение задач с помощью теоремы
- 16. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Методическая разработка
Рудаковой Татьяны Викторовны
Учителя математики МБОУ «Гимназия № 2»
Слайд 2Содержание
Теоретические факты:
а) пропорциональные отрезки в треугольниках
б)
отношение площадей треугольников.
Теорема Менелая.
Применение теоремы для решения задач.
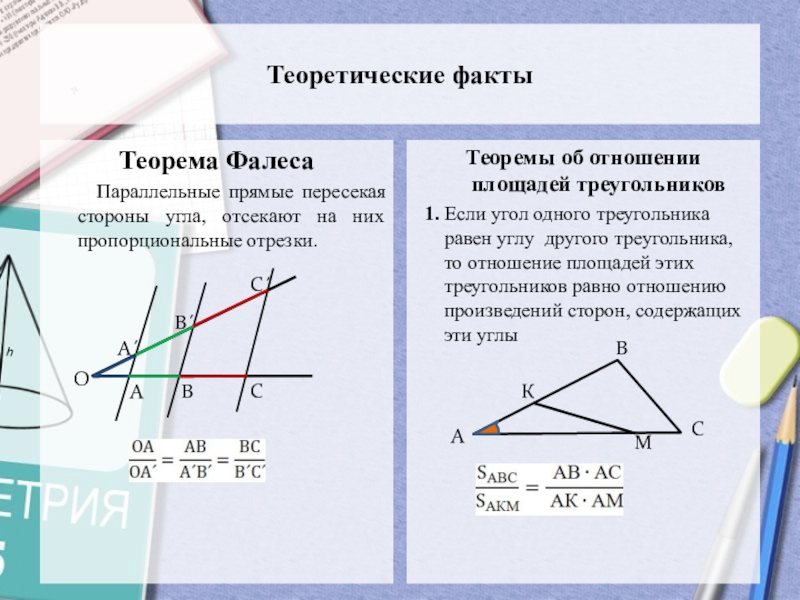
Слайд 3Теоретические факты
Теорема Фалеса
Параллельные прямые пересекая стороны
угла, отсекают на них пропорциональные отрезки.
Теоремы об отношении площадей треугольников
1. Если угол одного треугольника равен углу другого треугольника, то отношение площадей этих треугольников равно отношению произведений сторон, содержащих эти углы Слайд 4Теоремы об отношении площадей треугольников
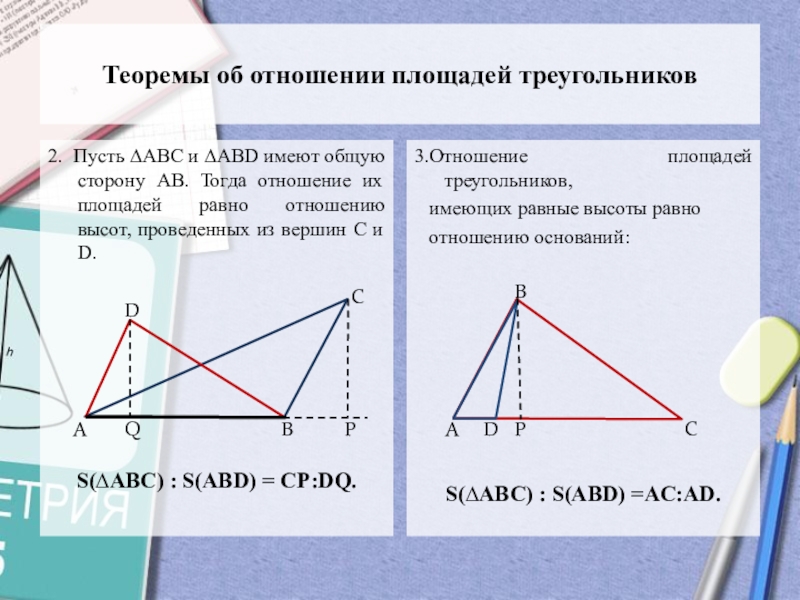
2. Пусть ∆АВС и ∆АВD имеют
общую сторону АВ. Тогда отношение их площадей равно отношению высот,
проведенных из вершин С и D.S(∆АВС) : S(АВD) = СР:DQ.
3.Отношение площадей треугольников,
имеющих равные высоты равно
отношению оснований:
S(∆АВС) : S(АВD) =AC:АD.
А
В
С
D
P
Q
А
В
С
D
P
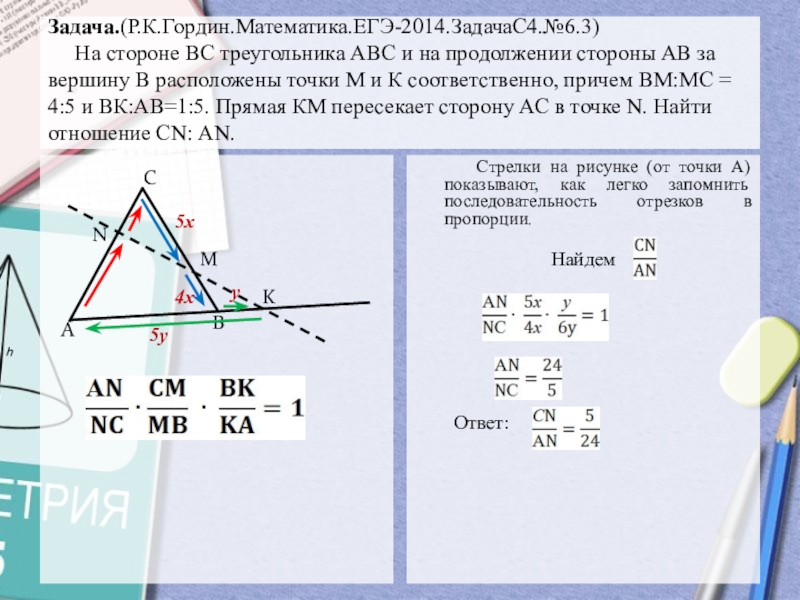
Слайд 5Задача.(Р.К.Гордин.Математика.ЕГЭ-2014.ЗадачаС4.№6.3) На стороне ВС треугольника
АВС и на продолжении стороны АВ за вершину В расположены
точки М и К соответственно, причем ВМ:МС = 4:5 и ВК:АВ=1:5. Прямая КМ пересекает сторону АС в точке N. Найти отношение СN: АN.Решение
Проведем ВР параллельно КМ.
По теореме Фалеса для угла NАК:
По теореме Фалеса для угла ВСР:
4. Итак, z=4d, тогда АN=6z=24d, значит СN:АN=5:24.
Ответ: 5:24
А
С
В
М
К
N
4х
5х
у
5у
Р
5z
z
N
4x
5d
4d
Слайд 6 Предложенный вариант решения задачи – один из традиционных,
без применения теоремы Менелая.
Рассмотрим другой (более рациональный) способ
решения, применяя указанную теоремуТеорема Менелая
Пусть на сторонах AB, BC и на продолжении стороны AC ∆ABC взяты соответственно точки С´, А´ и В´, не совпадающие с вершинами ∆ABC. Точки лежат на одной прямой тогда и только тогда, когда выполняется равенство
Для дальнейшего решения задач воспользуемся необходимым условием данной теоремы.
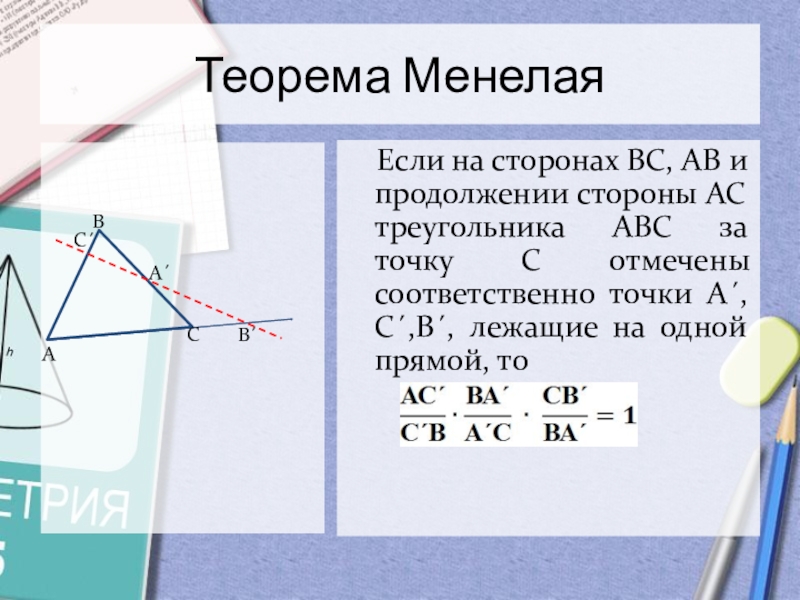
Слайд 7Теорема Менелая
Если на сторонах ВС, АВ и продолжении
стороны АС треугольника АВС за точку С отмечены соответственно точки
А´, С´,В´, лежащие на одной прямой, тоВ
А
С
В´
А´
С´
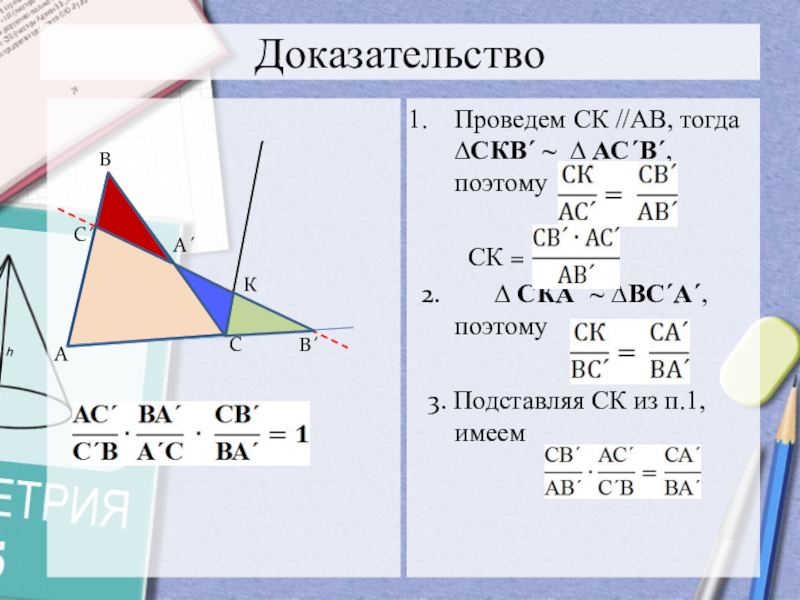
Слайд 8Доказательство
Проведем СК //АВ, тогда ∆СКВ´ ~ ∆ АС´В´, поэтому
СК =
2.
∆ СКА´ ~ ∆ВС´А´, поэтому 3. Подставляя СК из п.1, имеем
В
А
С
В´
К
А´
С´
Слайд 9 Задача.(Р.К.Гордин.Математика.ЕГЭ-2014.ЗадачаС4.№6.3) На
стороне ВС треугольника АВС и на продолжении стороны АВ за
вершину В расположены точки М и К соответственно, причем ВМ:МС = 4:5 и ВК:АВ=1:5. Прямая КМ пересекает сторону АС в точке N. Найти отношение СN: АN.
Стрелки на рисунке (от точки А) показывают, как легко запомнить последовательность отрезков в пропорции.
Найдем
Ответ:
А
С
В
N
M
K
4х
5х
у
5у
Слайд 10
Найти:
Ответ:
Задача. (Р.К.Гордин. Математика. ЕГЭ-2014. ЗадачаС4. №6.10)
В
треугольнике АВС АВ=с, ВС=а, АС=в. В каком отношении центр вписанной
окружности треугольника делит биссектрису СD?Решение:
Для треугольника ВСD и секущей АК:
Найдем ДА: =
ДА =
3. Найдем :
В
С
А
К
D
О
Слайд 11
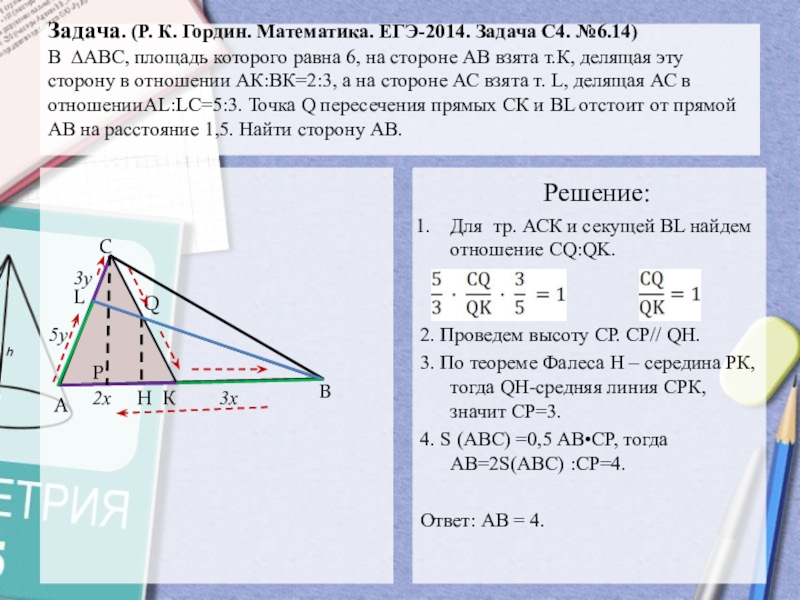
Задача. (Р. К. Гордин. Математика. ЕГЭ-2014. Задача С4.
№6.14) В ∆АВС, площадь которого равна 6, на стороне
АВ взята т.К, делящая эту сторону в отношении АК:ВК=2:3, а на стороне АС взята т. L, делящая АС в отношенииAL:LС=5:3. Точка Q пересечения прямых СК и ВL отстоит от прямой АВ на расстояние 1,5. Найти сторону АВ. Решение:
Для тр. АСК и секущей ВL найдем отношение CQ:QK.
2. Проведем высоту СР. СР// QH.
3. По теореме Фалеса Н – середина РК, тогда QH-средняя линия СРК, значит СР=3.
4. S (АВС) =0,5 АВ•СР, тогда АВ=2S(АВС) :СР=4.
Ответ: АВ = 4.
L
Q
H
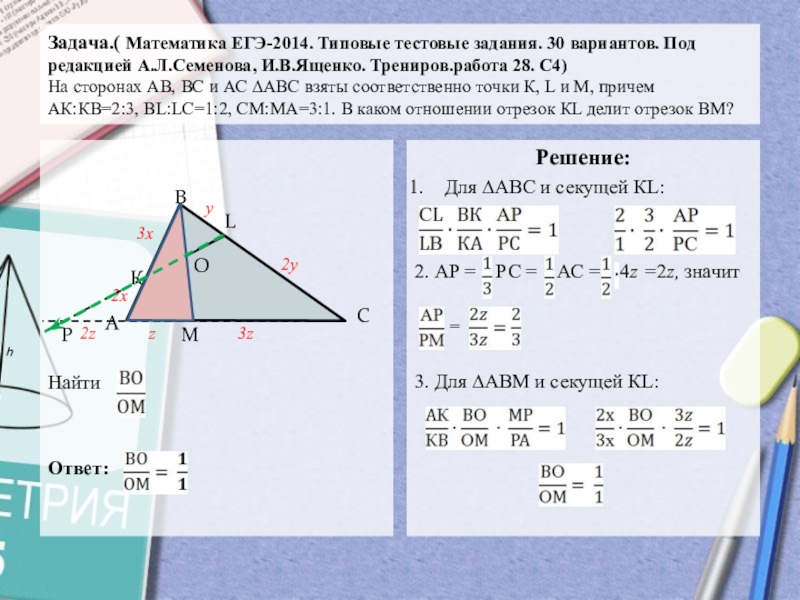
Слайд 12Задача.( Математика ЕГЭ-2014. Типовые тестовые задания. 30 вариантов. Под редакцией
А.Л.Семенова, И.В.Ященко. Трениров.работа 28. С4) На сторонах АВ, ВС и
АС ∆АВС взяты соответственно точки К, L и М, причем АК:КВ=2:3, ВL:LС=1:2, СМ:МА=3:1. В каком отношении отрезок КL делит отрезок ВМ?
Найти
Ответ:
Решение:
Для ∆АВС и секущей КL:
2. АР = РС = АС = 4z =2z, значит
=
3. Для ∆АВМ и секущей КL:
М
К
L
2х
3х
у
2у
3z
z
О
Р
2z
Слайд 13Задача. (Сайт А.А.Ларина. Тренировочный вариант №67. от 09.03.2014. С4) В
∆АВС на сторонах АВ, ВС, и СА отложены соответственно отрезки
АD =⅓ АВ, ВЕ = ⅓ ВС, СF = ⅓ CА. а) доказать, что , где М = АЕ ∩ СD, К = СD ∩ ВF, N = АЕ∩ВF. б) найти, какую часть от площади ∆АВС составляет площадь ∆MNK.а) докажем, что
Для ∆АВF и секущей DC:
2. Для ∆АЕС и секущей FВ:
3. Для ∆DBC и секущей ЕА аналогично
х
2х
у
2у
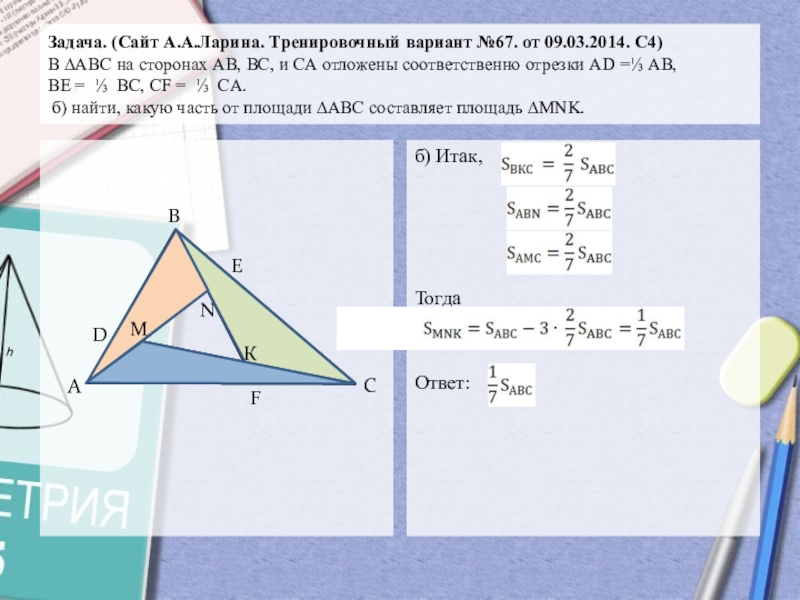
Слайд 14Задача. (Сайт А.А.Ларина. Тренировочный вариант №67. от 09.03.2014. С4) В
∆АВС на сторонах АВ, ВС, и СА отложены соответственно отрезки
АD =⅓ АВ, ВЕ = ⅓ ВС, СF = ⅓ CА. б) найти, какую часть от площади ∆АВС составляет площадь ∆MNK.б) Итак,
Тогда
Ответ:
А
В
С
D
E
F
М
N
K
М
К
Слайд 15Заключение Решение задач с помощью теоремы Менелая более рационально,
чем их решение другими способами, требующими дополнительных действий и построений,
которые не всегда оказываются очевидными. Теорема Менелая помогает быстро и оригинально решить задачи повышенной сложности, в том числе и задачи уровня С единого государственного экзамена.Используемая литература
ЕГЭ 2014.Математика. Задача С4. Гордин Р.К. Под ред. Семенова А.Л.2013г.
Математика. ЕГЭ-2014. Типовые тестовые задания. 30 вариантов. Под ред. А.Л.Семенова, И.В.Ященко. 2014г.
http://alexlarin.net/ege/2014/trvar67.html